Chapitres Maths en Terminale Générale
Cours sur le Dénombrement en Terminale générale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths de Terminale
Pour maximiser vos résultats au bac, il vous faudra maîtriser le chapitre sur le dénombrement. En effet, il s’agit d’un important chapitre du programme de Maths de Terminale, essentiel pour le bac mais aussi, si vous voulez plus tard intégrer les meilleures prépa MP. En cas de lacunes, des cours particuliers de maths pourront vous aider à dépasser vos difficultés et à arriver à un excellent niveau.
1. Opérations sur les ensembles en Terminale
1.1. Rappels sur les opérations sur les ensembles en Terminale :
![]() Si
Si ![]() est un ensemble, on dit que
est un ensemble, on dit que ![]() est une partie de
est une partie de ![]() ou un sous ensemble de
ou un sous ensemble de ![]() lorsque tout élément de
lorsque tout élément de ![]() est élément de
est élément de ![]() .
.
Dans ce cas, on écrit ![]() .
.
On dit aussi que ![]() est inclus dans
est inclus dans ![]() .
.
Un ensemble ![]() n’est pas inclus dans l’ensemble
n’est pas inclus dans l’ensemble ![]() s’il existe
s’il existe ![]() tel que
tel que ![]() .
.
L’ensemble vide noté ![]() est une partie de tout ensemble
est une partie de tout ensemble ![]() .
.
![]() Deux ensembles
Deux ensembles ![]() et
et ![]() sont égaux s’ils vérifient les conditions équivalentes :
sont égaux s’ils vérifient les conditions équivalentes :
![]()
![]() et
et ![]() ont les mêmes éléments
ont les mêmes éléments
![]()
![]() est élément de
est élément de ![]() ssi
ssi ![]() est élément de
est élément de ![]()
![]()
![]() et
et ![]() .
.
![]() Soient
Soient ![]() et
et ![]() deux parties de l’ensemble
deux parties de l’ensemble ![]() .
.
![]() La réunion de
La réunion de ![]() et
et ![]() est la partie de
est la partie de ![]() formée des éléments de
formée des éléments de ![]() qui appartiennent à
qui appartiennent à ![]() ou à
ou à ![]() :
:
![]() .
.
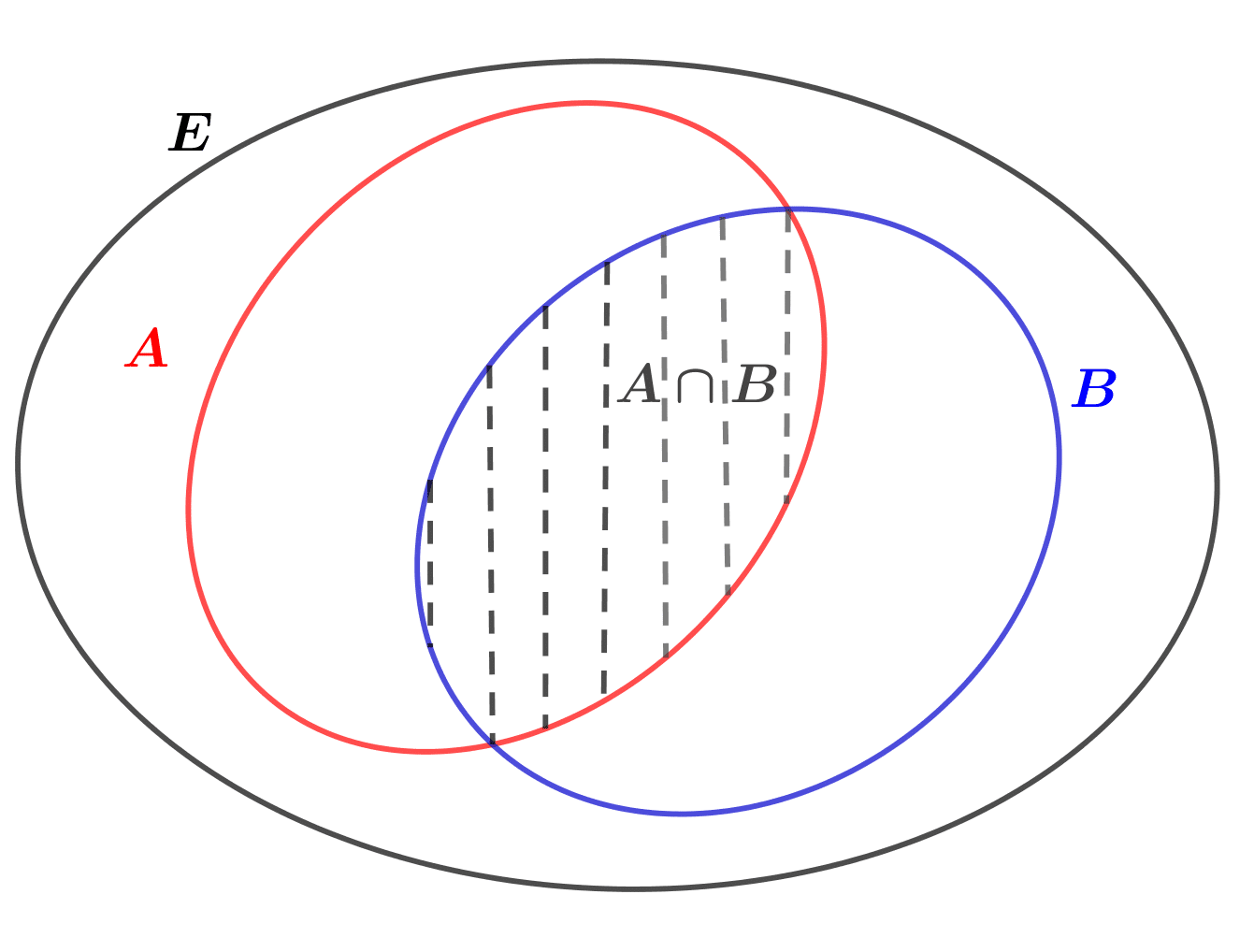
![]() L’intersection de
L’intersection de ![]() et
et ![]() est la partie de
est la partie de ![]() formée des éléments de
formée des éléments de ![]() qui appartiennent à
qui appartiennent à ![]() et à
et à ![]() :
:
![]() .
.
![]()
![]() et
et ![]() sont dits disjoints lorsque
sont dits disjoints lorsque ![]() .
.
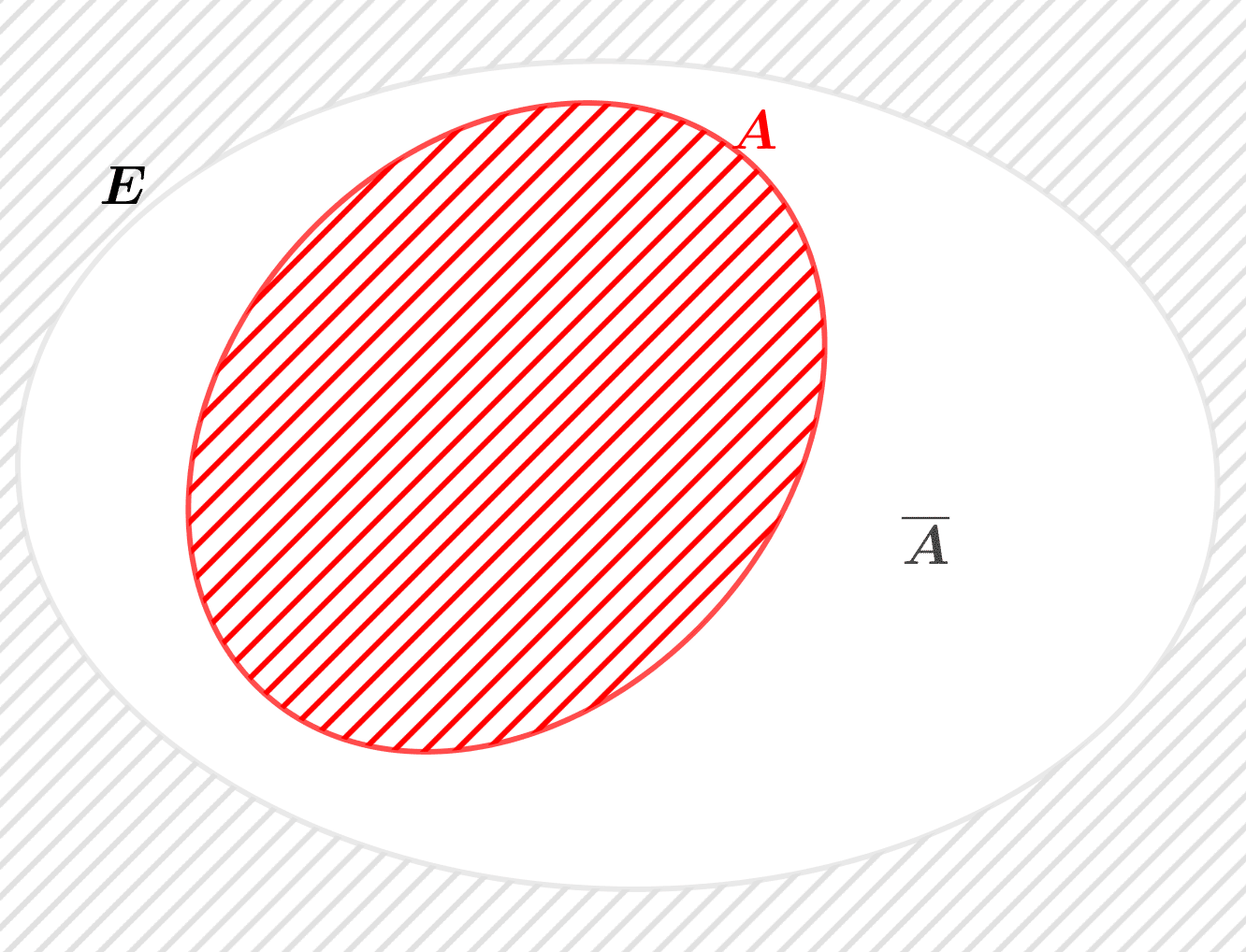
![]() Si
Si ![]() est une partie de l’ensemble
est une partie de l’ensemble ![]() ,
,
![]() le complémentaire de
le complémentaire de ![]() dans
dans ![]() est l’ensemble des éléments de
est l’ensemble des éléments de ![]() qui n’appartiennent pas à
qui n’appartiennent pas à ![]() :
: ![]()
![]()
![]() et
et ![]() sont disjointes
sont disjointes
![]()
![]() .
.
![]() Si
Si ![]() et
et ![]() sont des parties de l’ensemble
sont des parties de l’ensemble ![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
1.2. Produit cartésien en Terminale
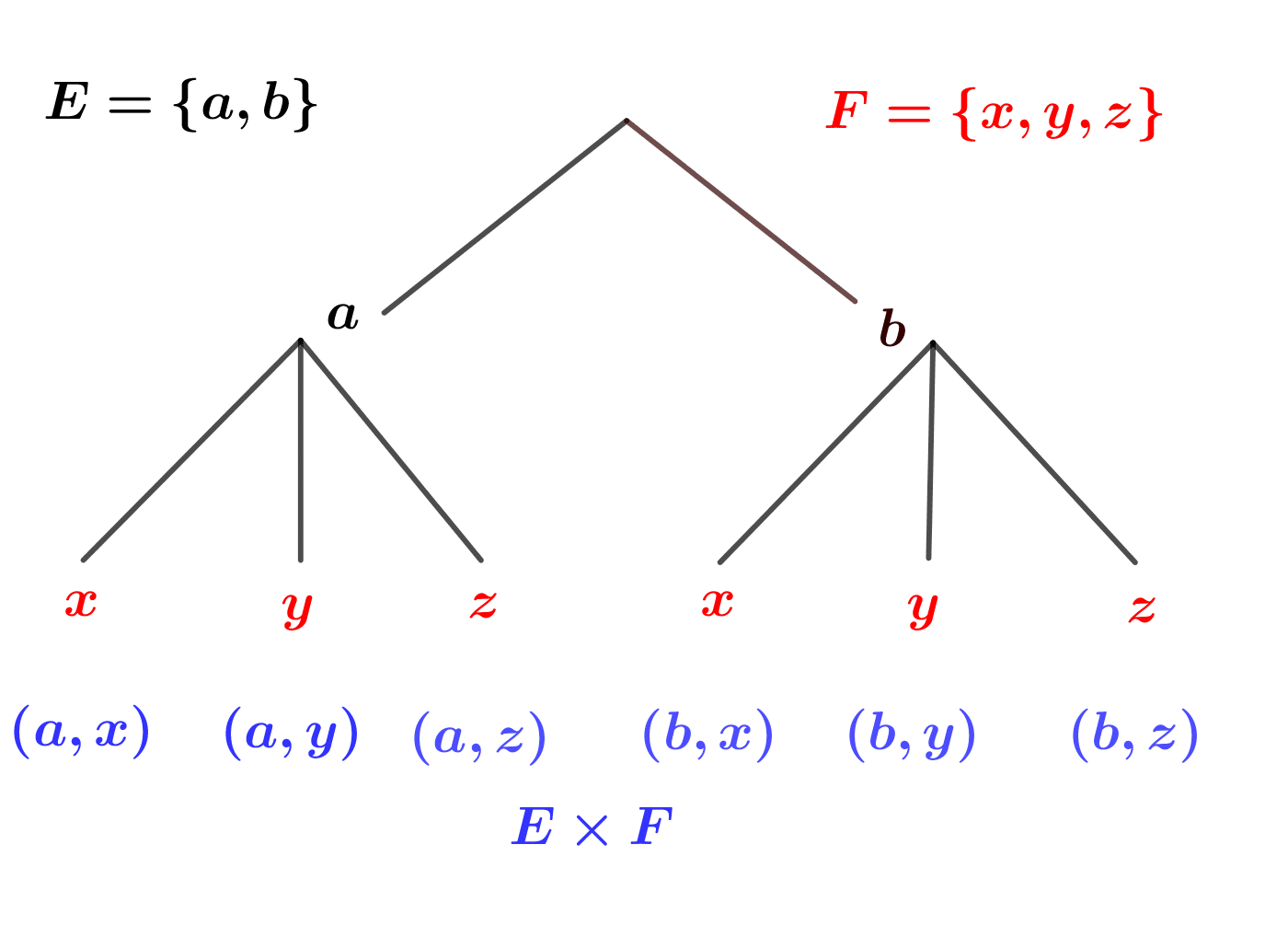
![]() Le produit cartésien des ensembles
Le produit cartésien des ensembles ![]() et
et ![]() est
est
![]() .
.
Les éléments de ![]() sont appelés couples.
sont appelés couples.
![]() ssi
ssi ![]() et
et ![]() .
.
![]() Le produit cartésien des ensembles
Le produit cartésien des ensembles ![]() ,
, ![]() et
et ![]() est
est
![]()
![]() .
.
Les éléments de ![]() sont appelés triplets .
sont appelés triplets .
![]() ssi
ssi ![]() ,
, ![]() et
et ![]() .
.
![]() Plus généralement si
Plus généralement si ![]() et si pour tout
et si pour tout ![]() ,
, ![]() est un ensemble, le produit cartésien des ensembles
est un ensemble, le produit cartésien des ensembles ![]() est noté
est noté
![]()
c’est l’ensemble des ![]() -uplets
-uplets
![]() lorsque pour tout
lorsque pour tout ![]() ,
, ![]() .
.
Dans le cas où pour tout ![]() ,
, ![]() , on note le produit cartésien
, on note le produit cartésien ![]() .
.
Un élément de ![]() est appelé
est appelé ![]() -uplet ou
-uplet ou ![]() -liste d’éléments de
-liste d’éléments de ![]() .
.
En géométrie, par exemple, vous avez déjà raisonné avec ![]() et
et ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Principe additif et multiplicatif en Terminale
Dans la suite, on suppose que l’on raisonne dans des ensembles ayant un nombre fini d’éléments. On dit alors qu’ils sont finis.
Si ![]() a
a ![]() éléments, on dit que le cardinal de
éléments, on dit que le cardinal de ![]() est égal à
est égal à ![]() et on note
et on note ![]() .
.
On pose ![]() .
.
Toute partie ![]() d’un ensemble fini
d’un ensemble fini ![]() est finie et
est finie et ![]() .
.
2.1. Principe additif en Terminale
![]() Si deux ensembles
Si deux ensembles ![]() et
et ![]() sont finis et disjoints,
sont finis et disjoints, ![]() est fini et
est fini et
![]() .
.
![]() Si
Si ![]() ensembles
ensembles ![]() sont finis et 2 à 2 disjoints,
sont finis et 2 à 2 disjoints, ![]() est fini et
est fini et
![]()
![]()
Application : Si ![]() est une partie de l’ensemble fini
est une partie de l’ensemble fini ![]() ,
,
![]() .
.
Méthode : Utiliser le principe additif pour dénombrer un ensemble ![]() , c’est écrire
, c’est écrire ![]() comme réunion de
comme réunion de ![]() (resp.
(resp. ![]() ) ensembles finis disjoints (resp. 2 à 2 disjoints) et utiliser l’un des deux résultats précédents.
) ensembles finis disjoints (resp. 2 à 2 disjoints) et utiliser l’un des deux résultats précédents.
Méthode pour dénombrer ![]() lorsque
lorsque ![]() , écrire
, écrire ![]() comme réunion des 3 ensembles, 2 à 2 disjoints,
comme réunion des 3 ensembles, 2 à 2 disjoints,
![]() ,
, ![]() et
et ![]() .
.
![]() est l’ensemble des éléments de
est l’ensemble des éléments de ![]() qui ne sont pas dans
qui ne sont pas dans ![]() , c’est aussi le complémentaire dans
, c’est aussi le complémentaire dans ![]() de
de ![]()
![]() est l’ensemble des éléments de
est l’ensemble des éléments de ![]() qui ne sont pas dans
qui ne sont pas dans ![]() , c’est aussi le complémentaire dans
, c’est aussi le complémentaire dans ![]() de
de ![]() .
.
2.2. Principe multiplicatif en Terminale
![]() Si deux ensembles
Si deux ensembles ![]() et
et ![]() sont finis,
sont finis, ![]() est fini et
est fini et
![]() .
.
![]() Si
Si ![]() ensembles
ensembles ![]() sont finis,
sont finis, ![]() est fini et
est fini et
![]()
![]() .
.
En particulier, si ![]() est un ensemble fini,
est un ensemble fini, ![]() .
.
Méthode : Utiliser le principe multiplicatif pour dénombrer un ensemble ![]() c’est écrire
c’est écrire ![]() comme produit cartésien de
comme produit cartésien de ![]() (resp.
(resp. ![]() ) ensembles finis et utiliser l’un des deux résultats précédents.
) ensembles finis et utiliser l’un des deux résultats précédents.
On utilise cette méthode
![]() lorsque l’on choisit successivement deux éléments dans deux ensembles disjoints
lorsque l’on choisit successivement deux éléments dans deux ensembles disjoints ![]() et
et ![]() : on cherche donc le nombre d’éléments de
: on cherche donc le nombre d’éléments de ![]() .
.
![]() lorsque l’on choisit
lorsque l’on choisit ![]() éléments en remettant après chaque tirage l’élément tiré dans l’ensemble
éléments en remettant après chaque tirage l’élément tiré dans l’ensemble ![]() .
.
On détermine un ![]() – uplet de
– uplet de ![]() , il y a donc
, il y a donc ![]() choix.
choix.
3. Les  -listes en Terminale
-listes en Terminale
3.1.  -liste et applications en Terminale
-liste et applications en Terminale
![]() On a vu que le nombre de
On a vu que le nombre de ![]() -listes d’un ensemble
-listes d’un ensemble ![]() de cardinal
de cardinal ![]() est le nombre de
est le nombre de ![]() -uplets de
-uplets de ![]() : soit
: soit ![]() .
.
![]() Le nombre d’applications d’un ensemble
Le nombre d’applications d’un ensemble ![]() de cardinal
de cardinal ![]() dans un ensemble
dans un ensemble ![]() de cardinal
de cardinal ![]() est le nombre de
est le nombre de ![]() -uplets d’éléments de
-uplets d’éléments de ![]() soit
soit ![]() .
.
![]() Soit
Soit ![]() un ensemble à
un ensemble à ![]() éléments. Le nombre de parties de
éléments. Le nombre de parties de ![]() est égal à
est égal à ![]() .
.
3.2. Factorielle d’un entier en Terminale
Soit ![]() , on appelle factorielle de
, on appelle factorielle de ![]() l’entier noté
l’entier noté ![]() avec
avec ![]()
et ![]()
alors pour tout ![]()
![]()
3.3.  -liste sans répétition en Terminale
-liste sans répétition en Terminale
![]() Soit
Soit ![]() et
et ![]() .
.
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() .
.
On appelle ![]() – liste sans répétition des éléments de
– liste sans répétition des éléments de ![]() tout
tout ![]() – uplet de
– uplet de ![]() formé d’éléments 2 à 2 distincts.
formé d’éléments 2 à 2 distincts.
![]() Soient
Soient ![]() et
et ![]() .
.
Le nombre de ![]() listes sans répétition des
listes sans répétition des ![]() éléments de
éléments de ![]() est égal à
est égal à
![]() .
.
3.4. Permutation en Terminale Générale
![]() Soit
Soit ![]() un ensemble de cardinal
un ensemble de cardinal ![]() .
.
On appelle permutation des éléments de ![]() toute
toute ![]() -liste sans répétition des éléments de
-liste sans répétition des éléments de ![]() .
.
![]() Il y a
Il y a ![]() permutations d’un ensemble à
permutations d’un ensemble à ![]() éléments.
éléments.
4. Combinaison en Terminale
4.1. Définition et valeur
![]() Soit
Soit ![]() un ensemble formé de
un ensemble formé de ![]() éléments. Soit
éléments. Soit ![]() .
.
On appelle combinaison de ![]() éléments de
éléments de ![]() toute partie de
toute partie de ![]() à
à ![]() éléments.
éléments.
![]() Soit
Soit ![]() et
et ![]() .
.
Le nombre de combinaisons de ![]() éléments d’une partie
éléments d’une partie ![]() à
à ![]() éléments est égal à
éléments est égal à ![]() .
.
![]()
![]() .
.
En particulier ![]() et
et ![]()
Il est conseillé de retenir aussi que ![]() .
.
![]() Application aux mots :
Application aux mots :
On écrit un mot de ![]() lettres à partir de
lettres à partir de ![]() et
et ![]() . Soit
. Soit ![]() .
.
Le nombre de mots de ![]() lettres où
lettres où ![]() est écrit
est écrit ![]() fois est égal à
fois est égal à ![]() .
.
![]() Application au nombre de chemins
Application au nombre de chemins
On effectue ![]() déplacements, à chaque déplacement, on a le choix entre un déplacement à gauche et un déplacement à droite.
déplacements, à chaque déplacement, on a le choix entre un déplacement à gauche et un déplacement à droite.
Le nombre de chemins de ![]() déplacements où l’on a effectué
déplacements où l’on a effectué ![]() déplacements à droite est égal à
déplacements à droite est égal à ![]() .
.
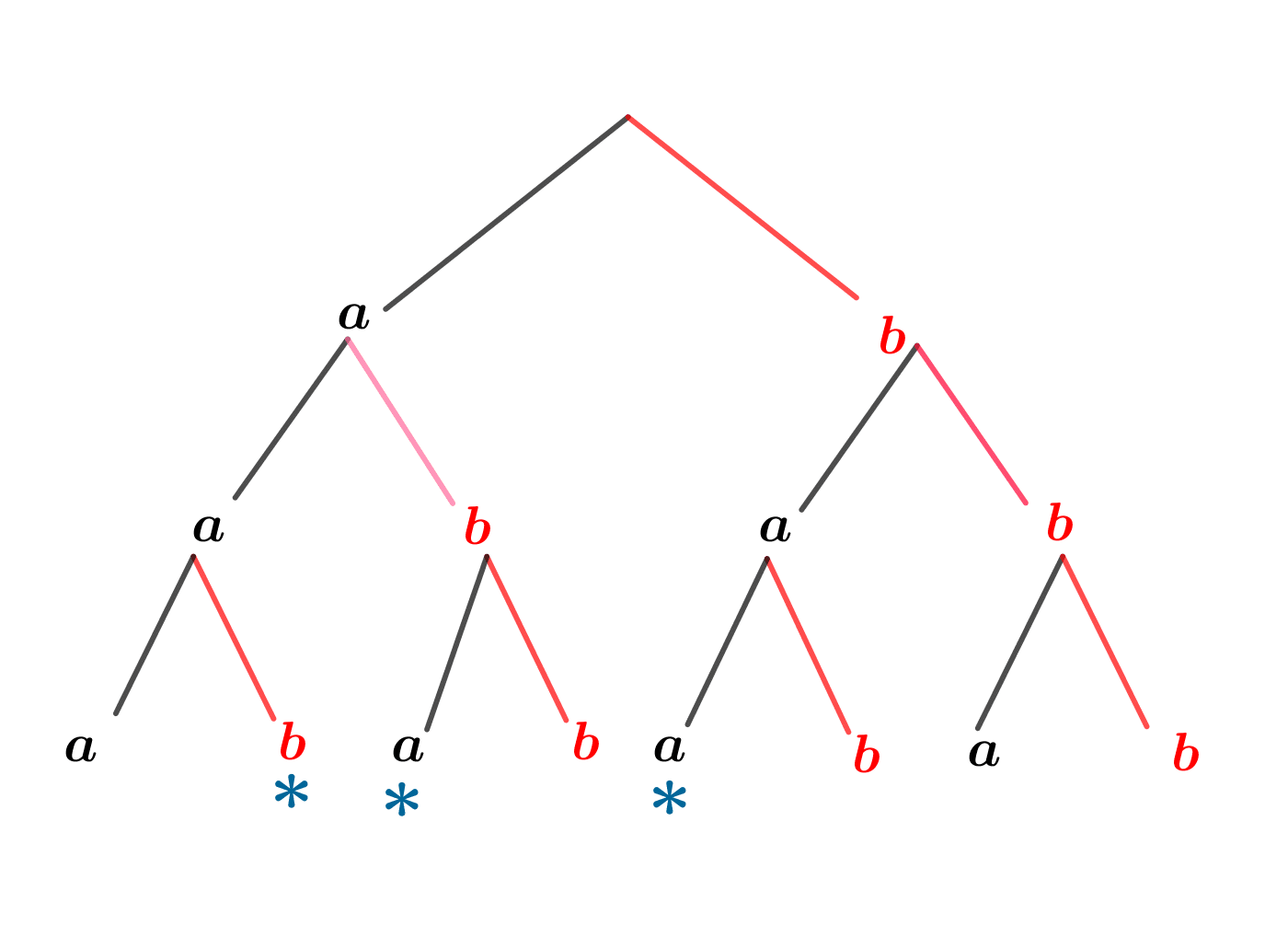
On peut s’aider par un arbre comme ci-dessous :
4.2. Propriétés des coefficients du binôme en Terminale
![]() Si
Si ![]() et
et ![]() ,
,
![]() .
.
![]() Formule du triangle de Pascal
Formule du triangle de Pascal
Soit ![]() . Si
. Si ![]() ,
,
![]() .
.
On peut obtenir les coefficients du binôme lorsque ![]() est faible (en général
est faible (en général ![]() ), en calculant le triangle de Pascal
), en calculant le triangle de Pascal
![]() Si
Si ![]() ,
, 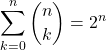
5. Quelques méthodes en complément
5.1 Utilisation du complémentaire en Terminale
Pour dénombrer ![]() « avoir au moins un élément vérifiant une propriété
« avoir au moins un élément vérifiant une propriété ![]() » (où
» (où ![]() ),
),
![]() En général il est plus simple de dénombrer le complémentaire
En général il est plus simple de dénombrer le complémentaire ![]() (c’est le cas lorsque le complémentaire se traduit par « sans ») et d’utiliser
(c’est le cas lorsque le complémentaire se traduit par « sans ») et d’utiliser ![]() .
.
![]() Lorsque le nombre maximum
Lorsque le nombre maximum ![]() d’éléments vérifiant la propriété
d’éléments vérifiant la propriété ![]() est faible, on peut envisager de noter
est faible, on peut envisager de noter ![]() « avoir
« avoir ![]() éléments vérifiant
éléments vérifiant ![]() » et écrire
» et écrire 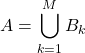 , les ensembles étant deux à deux disjoints,
, les ensembles étant deux à deux disjoints, 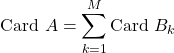
par le principe additif.
5.2. Autour de 
Soient ![]() et
et ![]() deux parties de
deux parties de ![]() .
.
![]() Pas de problème si
Pas de problème si ![]() car
car ![]()
Lorsque ![]() , on a plusieurs méthodes :
, on a plusieurs méthodes :
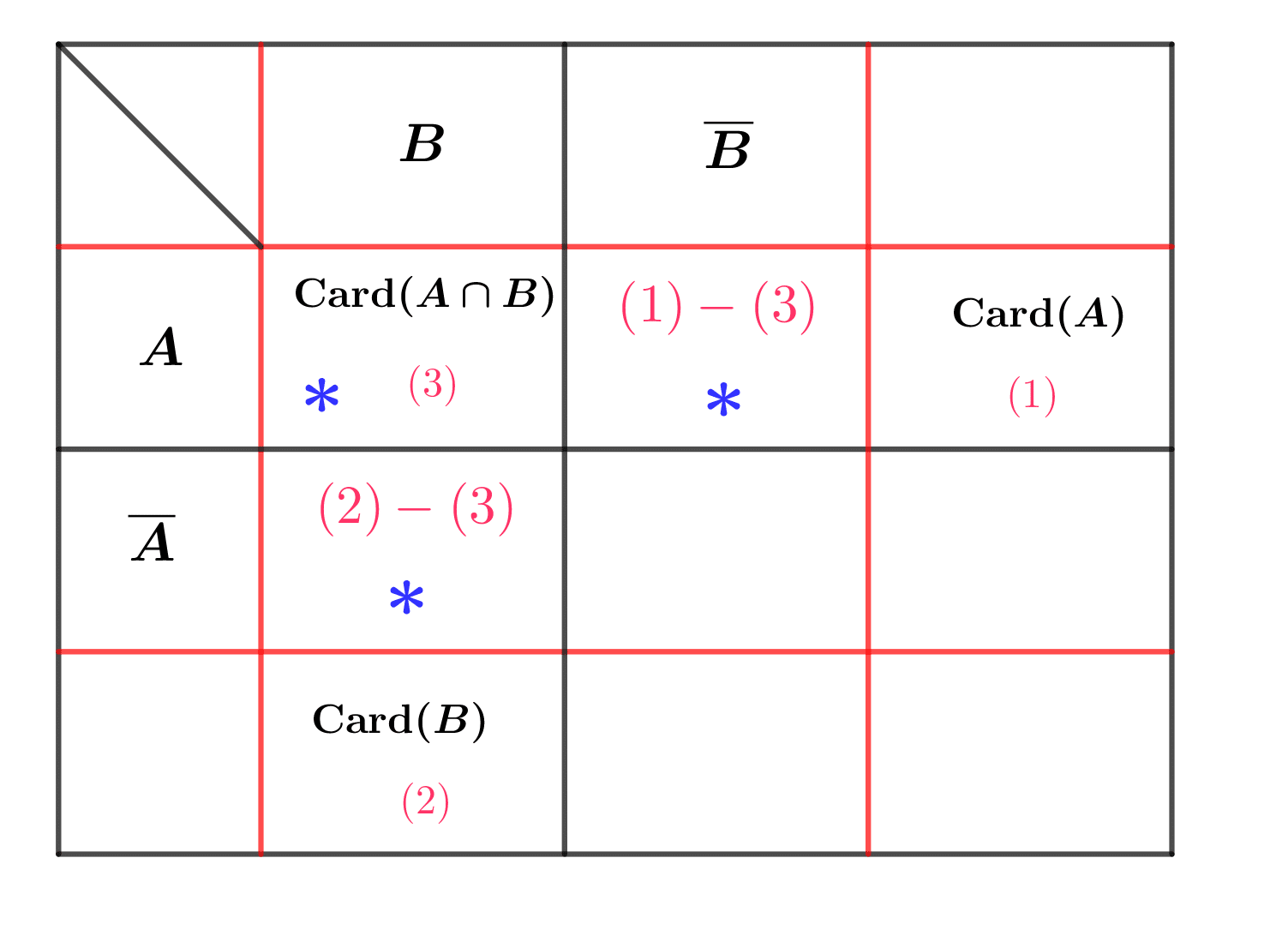
![]() Par utilisation d’un tableau à 4 lignes et 4 colonnes
Par utilisation d’un tableau à 4 lignes et 4 colonnes
Deux lignes intermédiaires ![]() et
et ![]() .
.
Deux colonnes intermédiaires ![]() et
et ![]() .
.
Dans les 4 cases intermédiaires du tableau, le cardinal de l’intersection de la ligne et de la colonne.
En fin des lignes 2 et 3, le cardinal de cette partie
En fin des colonnes 2 et 3, le cardinal de cette partie.
En dernière ligne, dernière colonne, ![]() .
.
5.3. Dénombrer des tirages en Terminale
Soit ![]() un ensemble de
un ensemble de ![]() éléments distincts. Soit
éléments distincts. Soit ![]() .
.
![]() tirer
tirer ![]() éléments de
éléments de ![]() avec remise entre chaque tirage, c’est choisir un élément de
avec remise entre chaque tirage, c’est choisir un élément de ![]() , il y a
, il y a ![]() tirages.
tirages.
![]() tirer
tirer ![]() éléments de
éléments de ![]() en une seule fois : on obtient une combinaison de
en une seule fois : on obtient une combinaison de ![]() éléments parmi
éléments parmi ![]() , il y a
, il y a ![]() tirages
tirages
![]() tirer successivement
tirer successivement ![]() éléments de
éléments de ![]() sans remise : on obtient une
sans remise : on obtient une ![]() – liste d’éléments 2 à 2 distincts de
– liste d’éléments 2 à 2 distincts de ![]() , il y en a
, il y en a ![]() .
.
5.4. Reconnaitre un modèle binomial en Terminale
On suppose que ![]() et
et ![]() sont des entiers tels que
sont des entiers tels que ![]() .
.
![]() Lorsque l’on répète
Lorsque l’on répète ![]() fois un tirage entre des éléments de
fois un tirage entre des éléments de ![]() catégories
catégories ![]() et
et ![]() , il y a
, il y a ![]() tirages donnant
tirages donnant ![]() fois un élément de catégorie
fois un élément de catégorie ![]() et
et ![]() éléments de catégorie
éléments de catégorie ![]() .
.
![]() Lorsque l’on répète
Lorsque l’on répète ![]() fois une expérience menant à deux résultats possibles
fois une expérience menant à deux résultats possibles ![]() et
et ![]() , le nombre de façons d’obtenir une suite de
, le nombre de façons d’obtenir une suite de ![]() expériences donnant
expériences donnant ![]() fois le résultat
fois le résultat ![]() est égal à
est égal à ![]() .
.
5.5. Utiliser un arbre en Terminale
L’illustration par un arbre est à réserver aux cas où l’énoncé demande explici- tement de représenter les différentes situations par un arbre ou pour des effectifs faibles.
![]() Pour représenter
Pour représenter ![]() , où
, où ![]() et
et ![]() , en partant de la racine, placer
, en partant de la racine, placer ![]() branches terminées par les
branches terminées par les ![]() éléments de
éléments de ![]() .
.
De chacune de ces extrémités, tracer ![]() branches terminées par les
branches terminées par les ![]() éléments de
éléments de ![]() .
.
En parcourant les ![]() branches, on obtient les
branches, on obtient les ![]() couples
couples ![]() de
de ![]()
![]() On peut aussi représenter les
On peut aussi représenter les ![]() – listes sans répétition des
– listes sans répétition des ![]() éléments de
éléments de ![]() .
.
![]() En partant de la racine, placer
En partant de la racine, placer ![]() branches terminées par les
branches terminées par les ![]() éléments de
éléments de ![]() .
.
![]() De chacune de ces extrémités, tracer
De chacune de ces extrémités, tracer ![]() branches menant aux
branches menant aux ![]() éléments de
éléments de ![]() n’ayant pas encore été tirés.
n’ayant pas encore été tirés.
![]() Puis une troisième série de branches issues de ces
Puis une troisième série de branches issues de ces ![]() branches etc…
branches etc…
![]() À l’issue du tracé, le parcours des
À l’issue du tracé, le parcours des ![]() branches donnent les
branches donnent les ![]() listes sans répétition des
listes sans répétition des ![]() éléments de
éléments de ![]() .
.
![]() Dans un modèle binomial.
Dans un modèle binomial.
Pour dénombrer dans une suite de ![]() épreuves ayant
épreuves ayant ![]() résultats (notés
résultats (notés ![]() et
et ![]() ici) , on peut aussi s’aider d’un arbre :
ici) , on peut aussi s’aider d’un arbre :
![]() On part de la racine, et on place 2 branches terminées par
On part de la racine, et on place 2 branches terminées par ![]() et
et ![]() .
.
![]() De chacune de ces 2 branches, par- tent 2 nouvelles branches terminées par
De chacune de ces 2 branches, par- tent 2 nouvelles branches terminées par ![]() et
et ![]()
![]() On recommence jusqu’à avoir tracé
On recommence jusqu’à avoir tracé ![]() branches successives.
branches successives.
On obtient un arbre à ![]() branches correspondant aux
branches correspondant aux ![]() listes de
listes de ![]() .
.
On peut ensuite pour ![]() donné suivre les branches donnant
donné suivre les branches donnant ![]() fois
fois ![]() et obtenir le nombre
et obtenir le nombre ![]() de branches contenant exactement
de branches contenant exactement ![]() fois
fois ![]() .
.
![]() Mots de longueur
Mots de longueur ![]() écrits avec
écrits avec ![]() lettres.
lettres.
On obtient le même principe lorsque l’on veut écrire les mots de ![]() lettres formés uniquement de
lettres formés uniquement de ![]() et de
et de ![]() .
.
Faire un arbre comme dans le cas précédent, en remplaçant ![]() par
par ![]() et
et ![]() par
par ![]() .
.
L’arbre a ![]() branches et on peut mettre en évidence les
branches et on peut mettre en évidence les ![]() branches formant des mots contenant exactement
branches formant des mots contenant exactement ![]() fois la lettre
fois la lettre ![]() .
.
Les Maths ayant un gros coefficient au bac, comme vous pouvez d’ailleurs le voir en consultant notre simulateur du Bac, il est important de bien suivre les cours et s’entraîner sur des exercices. N’hésitez donc pas à vous rendre sur les cours en ligne de maths de terminale pour vérifier vos connaissances, testez-vous par exemple sur les chapitres suivants :
- loi binomiale
- loi des grands nombres
- loi Normale, intervalle de fluctuation
- raisonnement par récurrence
- les suites
Au delà des cours particuliers, des cours en ligne et des exercices, vous pouvez également utiliser un autre support très utile : les annales du bac de maths. Elles vous serviront pour vous entraîner en conditions réelles et pour bien identifier les attendus de l’épreuve du bac.

