Chapitres du sous-test 2 du Tage Mage
Le théorème de Pythagore : cours, exemples, formules et réciproque
Résumé de cours Exercices et corrigés
Le théorème de Pythagore est le premier théorème important de géométrie vu au collège et doit être à ce titre maitrisé par ceux qui préparent le brevet, mais aussi par ceux qui s’entrainent au Tage Mage ou au Score Message. Le théorème de Pythagore comme le théorème de Thales manie les triangles, et en particulier les triangles rectangles. Sa réciproque permet de calculer la longueur des cotés du triangle rectangle.
Si vous avez des difficultés à comprendre ou maîtriser le théorème de Pythagore, vous pouvez faire appel à un prof de maths à domicile avec Groupe Réussite. Ce dernier vous aidera à totalement maîtriser le théorème de Pythagore à travers des cours sur mesure, des entraînements sur des exercices adaptés à votre niveau et des concours blancs de Tage Mage en maths pour une préparation optimale.
Définitions du théorème de Pythagore
- On dit qu’un triangle est rectangle si l’un de ses trois angles est un angle droit
- Dans un triangle rectangle, le côté opposé au sommet de l’angle droit est appelé hypoténuse ; c’est le côté le plus long du triangle.
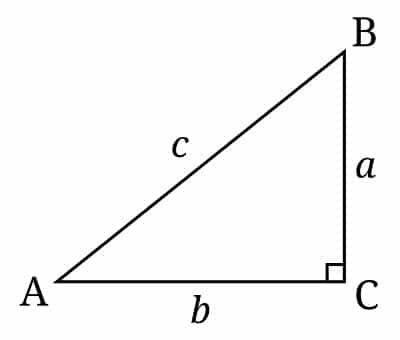
a et b sont des côtés de l’angle droit C
c est l’hypoténuse du triangle rectangle ABC
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Calculer la longueur d’un côté avec le théorème de Pythagore
Si un triangle est rectangle, alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux côtés de l’angle droit.
Exemple avec le théorème de Pythagore :
- Calculer la longueur de l’hypoténuse
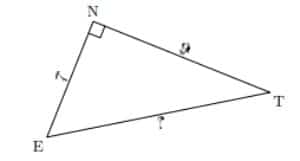
On sait que le triangle ENT est rectangle en N. On peut donc appliquer le théorème de Pythagore :
ET² = NT² + NE²
En remplaçant les longueurs connues par leurs valeurs, on obtient :
ET² = 9² + 7²
ET² = 81+49
ET² = 130
ET = ![]() ≈ 11,4
≈ 11,4
Donc la longueur du côté [ET] est 11,4 environ.
- Calculer la longueur d’un côté de l’angle droit

On pose a = 5 cm et c = 13 cm
On sait que le triangle ACB est rectangle en C. On peut donc appliquer le théorème de Pythagore :
AB² =AC²+BC²
En remplaçant les longueurs connues par leurs valeurs, on obtient :
13² =AC² +5²
169 =AC² +25
AC² = 169−25
AC² = 144
AC= ![]() = 12
= 12
Donc la longueur du côté [AC] est 12.
Démontrer qu’un triangle n’est pas rectangle avec Pythagore
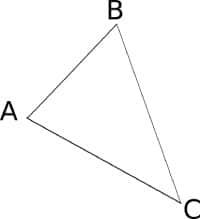
On pose AB = 6 cm, AC = 9 cm, BC = 12 cm.
- Démontrons que ce triangle n’est pas rectangle
Le côté le plus long est [BC] ; si le triangle était rectangle, ce côté serait l’hypoténuse.
D’une part, on a BC² = 12² = 144.
D’autre part, on a AC² + AB² = 9² + 6² = 81 + 36 = 117.
On constate que BC² ![]() AC²+AB².
AC²+AB².
Si le triangle était rectangle, d’après le théorème de Pythagore, on aurait l’égalité BC² = AC² + AB².
Ce n’est pas le cas, donc le triangle ABC n’est pas rectangle.
Démontrer qu’un triangle est rectangle: réciproque de Pythagore
Si, dans un triangle, le carré de la longueur du plus long côté est égal à la somme des carrés des longueurs des autres côtés, alors ce triangle est rectangle, et le côté le plus long est l’hypoténuse.

On pose AB = 12 cm, AC = 16 cm, BC = 20 cm
- Démontrons que ce triangle est rectangle
Le côté le plus long est [BC] ; si le triangle était rectangle, ce côté serait l’hypoténuse.
D’une part, on a BC² = 20² = 400.
D’autre part, on a AC²+AB² = 16² +12² = 256+144 = 400.
On constate que BC² =AC²+AB².
Donc, d’après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en A.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Les triplets de Pythagore
Au delà de l’application basique du théorème, il faut savoir que si un triangle possède certaines longueurs « spéciales », alors il est rectangle. Et réciproquement, on peut tout de suite trouver une longueur si on a deux des trois longueurs « spéciales » : ce sont les triplets de Pythagore.
- 1er triplet
Un triangle est rectangle lorsqu’il est de la forme suivante :
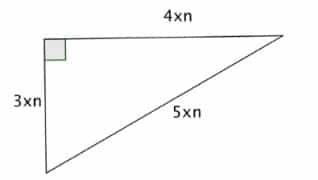
Application pour n = 1 :
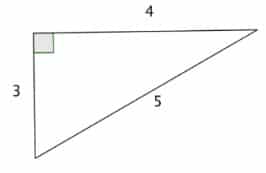 Le triangle est bien rectangle car 4² + 3² = 5²
Le triangle est bien rectangle car 4² + 3² = 5²
(la démonstration est assez simple puisque ![]() )
)
- 2ème triplet
Un triangle est rectangle lorsqu’il est de la forme suivante
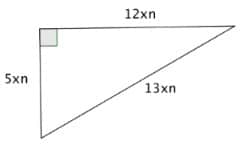
Application pour n = 1
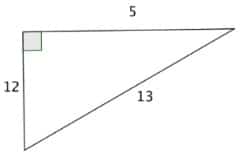
Le triangle est bien rectangle car 12² + 5² = 144 + 25 = 169 = 13². Et de même, ![]()
Ces triplets présentent une double utilité :
- Savoir qu’un triangle est rectangle si les longueurs sont ces triplets.
- Connaître directement la 3ème longueur d’un triangle rectangle dont les deux premières sont parmi ces triplets.
Exemple :
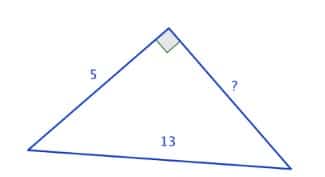
On remarque qu’il s’agit du 3ème triplet à savoir 5 – 12 – 13. Le côté mesurant 13 étant bien l’hypoténuse, le côté manquant vaut donc 12.
Découvrez et entraînez-vous sur d’autres chapitres du sous-test 2 du Tage Mage, afin d’être sûr d’obtenir un excellent score final :

