Chapitres Maths en Terminale Générale

Cours sur la chaîne de Markov en terminale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Résumé de cours : la chaîne de Markov en Terminale en Maths Expertes

Ce cours en ligne sur la chaîne de Markov au programme de terminale permet de revoir les notions importantes du cours pour réussir en terminale et obtenir de bons résultats au bac. Si vous êtes confronté à des difficultés en mathématiques, notre offre de prof de maths s’adresse spécialement aux étudiants de terminale pour les aider à surmonter ces obstacles.

1. Suites de matrices en Terminale

1.1. Suite géométrique de matrices colonnes

Soit $A$ une matrice carrée d’ordre $p$ (en général $p=$ 2 ou $p = 3$ .)

Si $U_0$ est une matrice colonne à $p$ lignes, on peut définir par récurrence une suite de matrices colonnes à $p$ lignes par la relation :

$\qquad$ si $n \in \mathbb{N}$ , $U_{n + 1} = A \, U_n \,$ .

Prop : avec les notations précédentes, pour tout entier $n\in \mathbb{N}, \,U_n = A ^n \ U_0\,$ .

1.2. Deuxième type de suites de matrices colonnes

Soit $A$ une matrice carrée d’ordre $p$ (en général $p=$ 2 ou $p = 3$ ) et $B$ une matrice colonne à $p$ lignes

Si $U_0$ est une matrice colonne à $p$ lignes, on peut définir par récurrence une suite de matrices colonnes à $p$ lignes par la relation :

$\quad$ si $n \in \mathbb{N}$ , $U_{n + 1} = A \, U_n + B$ .

Méthode d’étude
S’il existe une matrice colonne $C$ à $p$ lignes telle que $C = A \, C + B$ , en formant $V_n = U_n - C$ , on définit une suite de matrices colonnes telle que pour tout entier

$n$ , $V_ {n + 1} = A \, V_n$

donc $V_n = A^n \, V_0$

soit $\qquad \quad U_n - C = A ^n \,\left (U_0 - C \right )$ .

1.3. Pour des matrices lignes en terminale

Soit $A$ une matrice carrée d’ordre $p$ (en général $p=$ 2 ou $p = 3$ .)

Si $L_0$ est une matrice ligne à $p$ colonnes, on peut définir par récurrence une suite de matrices lignes à $p$ colonnes par la relation :

$\quad$ si $n \in \mathbb{N}$ , $L_{n + 1} = L_n\, A$ .

Prop : avec les notations précédentes, pour tout entier $n\in \mathbb{N}, \,L_n = L_0\, A ^n \,$ .

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

2. La chaîne de Markov en Maths expertes

2.1. Graphe probabiliste en terminale

Définition 1 : Un graphe orienté est dit pondéré lorsque chaque arête est affectée d’un nombre réel positif, appelé poids de cette arête.

Définition 2 : Un graphe probabiliste est un graphe orienté pondéré où tous les poids sont compris entre 0 et $1$ et où la somme des poids des arêtes issues d’un même sommet est égale à 1 .

Les sommets du graphe sont appelés états.

exemple d’un graphe probabiliste à 3 états.

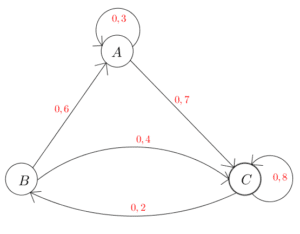
2.2. Définition d’une chaîne de Markov en Terminale Générale

Définition : On considère une suite $(X_n)_n$ de variables aléatoires permettant de modéliser l’évolution par étapes d’un système présentant $k$ états.

$\ast$ à l’étape $0$ , la loi de probabilité de $X_0$ s’appelle la distribution initiale du système.
$\ast$ à l’étape $n$ , la loi de probabilité de $X_n$ s’appelle la distribution après $n$ transitions.

Lorsque, à chaque étape, la probabilité de transition d’un état à un autre ne dépend pas de $n$ , on dit que la suite $(X_n)$ est une chaîne de Markov.

Conséquence : à une chaîne de Markov à $k$ états, on peut associer
$\ast$ un graphe probabiliste où les sommets sont les états du système aléatoire et le poids de l’arête liant un état à un autre est égal à la probabilité de transition de cet état à l’autre.
$\ast$ la matrice de transition de ce graphe probabiliste.

En pratique, on supposera dans la suite que $k = 2$ ou $k = 3$ .

3. Représentation d’une chaîne de Markov à l’aide d’une suite de matrices

Propriété 1.

Soit une chaîne de Markov à $k$ ( $k = 2$ ou $k = 3$ ) états.

On note $P$ la matrice de transition de associée.

Pour tout $n \in \mathbb{N}^*$ , si $(i,j) \in [\![1 , k]\!]^2$ , la probabilité de passer de l’état $i$ à l’état $j$ en $n$ étapes est égale au terme $p_{i,j} ^{(n)}$ de la ligne $i$ et colonne $j$ de la matrice $P ^n$ .

On note la probabilité conditionnelle de $B$ relative à $A$ (soit $\mathbb{P} _A (B)$ ) sous la forme $\mathbb{P}(B \, \mid \, A)$ .

On fait la démonstration lorsque $\mathbb{P}(X_0 = i) \neq 0$ si $i \in \{1 , 2\}$ .

Les variables aléatoires $X_n$ sont à valeurs dans $\{1 , 2\}$ .

Si $n \in \mathbb{N}^*$ , on note $\mathcal{P}(n)$ :

la matrice $P ^n$ est égale à

$\begin{pmatrix} \mathbb{P}(X_n = 1 \,\mid\, X_0 = 1) & \mathbb{P}(X_n = 2 \,\mid\, X_0 = 1)\\ \mathbb{P}(X_n = 1 \,\mid\, X_0 = 2) & \mathbb{P}(X_n = 2 \,\mid\, X_0 = 2) \end{pmatrix}$

$\bullet$ Initialisation

Pour $n = 1$ :
$\begin{pmatrix} \mathbb{P}(X_1 = 1 \,\mid\, X_0 = 1) & \mathbb{P}(X_1 = 2 \,\mid\, X_0 = 1)\\ \mathbb{P}(X_1 = 1 \,\mid\, X_0 = 2) & \mathbb{P}(X_1 = 2 \,\mid\, X_0 = 2) \end{pmatrix}$
est par définition la matrice $P$ de transition qui exprime la transition en 1 étape.

Donc $\mathcal{P}(1)$ est vraie.

$\bullet$ Hérédité
On suppose que $\mathcal{P}(n)$ est vraie pour un entier $n \geqslant 1$ donné.

$\ast$ Calcul préliminaire : $A , B , C$ sont trois événements et $\mathbb{P}(A) \neq 0$ .

Par la formule des probabilités totales,

$\mathbb{P} (B \cap A) =$ $\qquad \mathbb{P} (B \cap C \, \cap \, A) + \mathbb{P} (B \cap \, \overline{C} \, \cap \,A)$

donne

$\mathbb{P} (B \cap A) = \mathbb{P} (B \mid\, C \cap \, A)\, \mathbb{P} (C \mid A) \, \mathbb{P}(A)$ $\qquad \qquad +\, \mathbb{P} (B \mid \overline{C} \, \cap A)\, \mathbb{P} (\overline{C} \mid A) \, \mathbb{P}(A)$

et en divisant par $\mathbb{P}(A) \neq 0$

$\mathbb{P} (B \mid A) = \mathbb{P} (B \mid C \cap \, A)\, \mathbb{P} (C \mid A)$

$\qquad \qquad +\, \mathbb{P} (B \mid \overline{C} \, \cap A)\, \mathbb{P} (\overline{C} \mid A)$

$\ast$ Application :

Soient $i$ et $j$ dans $\{ 1 , 2\}^2$

On calcule la probabilité de passer de l’état $i$ à l’état $j$ en $n + 1$ transitions.

On applique la formule précédente avec :

$B = (X_{n + 1} = j)$ , $A = (X_{0} = i)$ , $C = (X_{n } = 1)$ et $\overline{C} = (X_{n + 1} = 2)$
$\mathbb{P}(X_{n + 1} = j \,\mid\, X_0 = i)$ $= \mathbb{P}(X_{n + 1} = j \mid X_n = 1 \,\cap \, X_0 = i)$ $\qquad \qquad \times \, \mathbb{P}( X_n = 1 \,\mid \, X_0 = i)$ $\;\; +\, \mathbb{P}(X_{n + 1} = j \mid X_n = 2 \,\cap \, X_0 = i)$ $\qquad \qquad \times\, \mathbb{P}( X_n = 2 \,\mid \, X_0 = i)$

Comme on a une chaîne de Markov

$\mathbb{P}(X_{n + 1} = j \mid X_n = 1 \,\cap \, X_0 = i)$ $\qquad = \mathbb{P}(X_{n + 1} = j \mid X_n = 1 ) = p_{1 ,j}$

et $\mathbb{P}(X_{n + 1} = j \mid X_n = 2 \,\cap \, X_0 = i)$ $\qquad = \mathbb{P}(X_{n + 1} = j \mid X_n = 2 ) = p_{2 , j}$

donc les relations s’écrivent en utilisant l’hypothèse de récurrence

$\mathbb{P}(X_{n + 1} = j \,\mid\, X_0 = i)$ $\qquad \qquad = p_{1 ,j}\, p_{i , 1}^{(n)} + p_{2 ,j}\, p_{i , 2 }^{(n)}$

soit aussi $p_{i , 1}^{(n)}\, p_{1 ,j} + p_{i , 2 }^{(n)} \, p_{2 ,j}\,$ .

On reconnait le terme d’indice $(i,j)$ du produit matriciel $P^n \times P$

donc $\mathbb{P}(X_{n + 1} = j \,\mid\, X_0 = i) = p_{i,j}^{(n + 1)}$

ce qui prouve la relation au rang $n + 1$ .

$\bullet$ Conclusion :

la propriété est vraie par récurrence sur $n \in \mathbb{N }^*$ .

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

Afin de bien se prépare au bac utilisez les annales de bac pour vous entraînez et tester vos connaissances sur des exercices types. Les cours particuliers en maths sont également un bon moyens de travailler pour obtenir les notes souhaitées et une mention.

N’oubliez pas également d’utiliser les différents cours en ligne de maths au programme de terminale pour vous aider dans vos révisions avant le bac, vérifiez par exemple, votre niveau de connaissances sur les chapitres de maths qui suivent :

Cours sur la chaîne de Markov en terminale

Résumé de cours : la chaîne de Markov en Terminale en Maths Expertes

1. Suites de matrices en Terminale

1.1. Suite géométrique de matrices colonnes

1.2. Deuxième type de suites de matrices colonnes

1.3. Pour des matrices lignes en terminale

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

2. La chaîne de Markov en Maths expertes

2.1. Graphe probabiliste en terminale

2.2. Définition d’une chaîne de Markov en Terminale Générale

3. Représentation d’une chaîne de Markov à l’aide d’une suite de matrices

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Cours sur la chaîne de Markov en terminale

Résumé de cours : la chaîne de Markov en Terminale en Maths Expertes

1. Suites de matrices en Terminale

1.1. Suite géométrique de matrices colonnes

1.2. Deuxième type de suites de matrices colonnes

1.3. Pour des matrices lignes en terminale

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

2. La chaîne de Markov en Maths expertes

2.1. Graphe probabiliste en terminale

2.2. Définition d’une chaîne de Markov en Terminale Générale

3. Représentation d’une chaîne de Markov à l’aide d’une suite de matrices

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour réussir sa scolarité

En ligne ou à domicile

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Les meilleurs profs de maths pour
réussir sa scolarité