Chapitres Maths en Terminale Générale

Cours sur les dérivées et la convexité en Terminale Générale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Cours en ligne sur le chapitre des dérivées et des fonctions convexes au programme de maths en Terminale. Ce chapitre est à maîtriser obligatoirement pour réussir en terminale et avoir de bons résultats au bac.

Pour se préparer au bac du mieux possible, il est fortement recommandé aux élève de terminale quel que soit leur niveau, de suivre des cours particuliers en maths.

1. Retour sur les cours de première

1.1. Définitions de fonctions sur les dérivées et la convexité

$\bullet$ Soit $f$ une fonction réelle définie sur un intervalle $I$ contenant $a$ .
$f$ est dérivable en $a$ ssi la fonction $\tau$ définie pour $x \in I$ et $x \neq a$ par $\qquad \quad \tau(x) = \displaystyle \frac {f(x) - f(a)} {x - a}$
admet une limite finie $L$ en $a$ .
$L$ = le nombre dérivé de la fonction $f$ en $a$
$\tau(x)$ est le taux d’accroissement de la fonction $f$ en $x$ .

$\bullet$ S’il existe un réel $L_d$ tel que $\qquad \displaystyle \lim_{x \to a ^{+}} \frac {f(x) - f(a)} {x - a} = L_d\,$ ,
$f$ est dite dérivable à droite en $a$ et son nombre dérivé à droite en $a$ $L_d$ est noté $f'_d(a)$ .

$\bullet$ S’il existe un réel $L_g$ tel que $\qquad \displaystyle \lim_{x \to a ^{-}} \frac {f(x) - f(a)} {x - a} = L_g\,$ ,
$f$ est dite dérivable à gauche en $a$ et son nombre dérivé à gauche en $a$ $L_g$ est noté $f'_g(a)$ .

$\bullet$ Si $a \in I$ n’est pas une borne de $I$ , $f$ est dérivable en $a$ ssi $f$ est dérivable à droite et à gauche en $a$ et si $\qquad \qquad f'_d(a) = f'_g(a)$ .

$\bullet$ Si $I = [a , b]$ , $f$ est dérivable à droite en $a$ ssi $f$ est dérivable en $a$ .
Si $I = [b , a]$ , $f$ est dérivable à gauche en $a$ ssi $f$ est dérivable en $a$ .

À savoir : la fonction $x \mapsto \vert x \vert$ n’est pas dérivable en $0$ , mais elle est dérivable à droite et à gauche en $0$ avec : $f'_d(0) = 1$ et $f'_g(0) = - 1$ .

1.2. Interprétation des fonctions dérivées en Terminale Générale

$\bullet$ Si $f$ est dérivable en $a$ , le graphe de $f$ admet une tangente en $(a , f(a))$ d’équation $\boxed{ y = f(a) + f'(a) (x - a)}$
La tangente est la position limite des sécantes $M(a) M(x)$ lorsque $x$ tend vers $a$ , en notant $M(x)$ le point de coordonnées $(x , f(x))$ .

$\bullet$ Si $f$ est continue sur $[a , b[$ et si $\displaystyle \lim_{x \to a} \frac {f(x) - f(a)} {x - a} = \infty$ , le graphe de $f$ admet une tangente verticale (à droite) en $(a , \, f(a))$ .
On raisonne de même pour une tangente verticale à gauche d’un point.

1.3. La fonction dérivée et son utilisation

$\bullet$ D: si $f : I \to \mathbb{R}$ est dérivable en tout point de $I$ , la fonction dérivée de $f$ est la fonction $f' : I \to \mathbb{R}, x \mapsto f'(x)$ .

$\bullet$ Dérivée et variation
Soit $f$ une fonction définie et dérivable sur l’intervalle $I$ à valeurs réelles.
$\ast$ $f$ est constante sur $I$ ssi pour tout $x \in I, \,f'(x) = 0$ .
$\ast$ $f$ est croissante sur $I$ ssi pour tout $x \in I,\, f'(x) \geqslant 0$ .
$\ast$ $f$ est décroissante sur $I$ ssi pour tout $x \in I, \,f'(x) \geqslant 0$ .

$\bullet$ Dérivée et extremum
Soit $f$ une fonction admettant un extremum en $a \in I$ , où $a$ n’est pas une borne de $I$ .
Si $f$ est dérivable en $a$ , $f'(a) = 0$ .

La réciproque est fausse comme dans l’exemple $f : x \mapsto x^3$ , la dérivée s’annule en $0$ et $f$ n’admet pas d’extremum en $0$ .

$\bullet$ Programme de Terminale : Si $f$ est dérivable en $a$ , $f$ est continue en $a$ .

1.4. La fonction dérivée et son utilisation

$\bullet$ Si $u$ et $v$ sont dérivables sur $I$ ,
$\ast$ $u + v$ est dérivable sur $I$ et $\qquad \qquad (u + v)' = u' + v'$
$\ast$ Si $k \in \mathbb{R}$ , $k \, u$ est dérivable sur $I$ et
$\qquad \qquad (k \, u)' = k \, u'$
$\ast$ $u \, v$ est dérivable sur $I$ et $\qquad \qquad (u \, v) ' = u' \, v + u \, v'$ .

$\bullet$ Si $u$ et $v$ sont dérivables sur $I$ et si $v$ ne s’annule pas sur $I$ ,
$\ast$ $\displaystyle \frac 1 v$ est dérivable sur $I$ et $\qquad \qquad \displaystyle \left ( \frac 1 v \right ) ' = \frac {- v'} {v ^2}$
$\ast$ $\displaystyle \frac u v$ est dérivable sur $I$ et $\qquad \qquad \displaystyle \left ( \frac u v \right ) ' = \frac { u' v - u \, v'} {v ^2}$ .

$\bullet$ $f : \mathbb {R} ^{+} \to \mathbb{R}, \, x \mapsto \sqrt{x}$ est dérivable sur $\mathbb{R} ^{+*}$ et si $x > 0,\, f'(x) = \displaystyle \frac 1 {2 \, \sqrt{x} }$ .

$\bullet$ Soit $f$ dérivable sur $I$ . Soient $a , b$ deux réels avec $a \neq 0$ .
On note $J = \{ x \in \mathbb{R}\, /\, a\, x + b \in I \}$ .
On définit $g : J \to \mathbb{R },\, x \mapsto f(a \, x + b)$ .
$g$ est dérivable sur $J$ et
$\quad$ si $x \in J, \, g'(x) = a f'(a \, x + b)$ .

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

2. Dérivées d’une fonction composée en Terminale Générale

2.1. Théorème de composition en terminale

Si $v$ est une fonction dérivable sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ , si la fonction $u$ est dérivable sur l’intervalle $J$ à valeurs dans $\mathbb{R}$ et si pour tout $x \in I, v(x) \in J$ , la fonction $u \circ v$ est définie sur $I$ et dérivable sur $I$ et pour tout $x \in I,$ $\qquad (u \circ v)'(x) = v'(x) \, u'(v(x))$ .
ce que l’on écrit sous la forme $\qquad \quad (u \circ v)' = v' \, . \, u' \circ v$ .

2.2. Les dérivées à connaître en terminale

On suppose que $u$ est dérivable sur $I$ à valeurs dans $\mathbb{R}$
$\ast$ pour tout $n \in \mathbb{N}^ *$
$\qquad \qquad (u^n)' = n \, u' \, u^{n - 1}$ .

$\ast$ si $u$ ne s’annule pas,
pour tout $n \in \mathbb{N}^ *$ , $\displaystyle \left ( \frac 1 {u^n} \right) ' = \displaystyle \frac {- n\, u'} { u^{n + 1}}$ .

$\ast$ on note $\textrm{e} ^u : I \to \mathbb{R }, x \mapsto \textrm{e} ^{u(x)}$ , $\qquad \qquad \left ( \textrm{e} ^u \right ) ' = u' \, \textrm{e} ^u$ .

$\ast$ On suppose que $u$ est à valeurs strictement positives sur $I$ .
On note $\sqrt{u} : I \to \mathbb{R}, x \mapsto \sqrt{u(x)}$ , $\qquad \qquad \left ( \sqrt{u} \right ) ' = \displaystyle \frac {u'} {2\, \sqrt{u}}$ .

$\ast$ On note $\cos u : t \mapsto \cos(u(t))$ et $\sin u : t \mapsto \sin(u(t))$
$\qquad \qquad (\cos u)' = - u' \, \sin u$ $\qquad \qquad (\sin u) ' = u' \, \cos u$ .

3. La convexité en Terminale Générale

3.1. Dérivée seconde

Soit $f : I \to \mathbb{R}$ une fonction dérivable, si $f'$ est dérivable sur $I$ , on dit que $f$ admet une dérivée seconde sur $I$ et on note $f'' = (f')'$ .

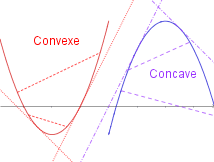
3.2. Fonction convexe et fonction concave

$\bullet$ Soit $f$ une fonction définie sur l’intervalle $I$ . On note $\Gamma$ son graphe.
$\ast$ $f$ est convexe lorsque pour tout $(a , b) \in I^2$ avec $a < b$ , la courbe $\Gamma$ est située sous la corde $[A\, B]$ où $A(a , f(a))$ et $B(b , f(b))$ .
$\ast$ $f$ est concave lorsque pour tout $(a , b) \in I^2$ avec $a < b$ , la courbe $\Gamma$ est située au dessus de la corde $[A \,B]$ où $A(a , f(a))$ et $B(b , f(b))$ .

$\bullet$ Soit $f$ une fonction deux fois dérivable sur l’intervalle $I$ à valeurs réelles.
Il y a équivalence entre
$\ast$ $f$ est convexe sur $I$
$\ast$ $f'$ est croissante sur $I$
$\ast$ $f''$ est à valeurs positives ou nulles
$\ast$ pour tout $a \in I$ , le graphe $\Gamma$ de $f$ est situé au dessus de la tangente en $(a ,\, f(a))$ à la courbe $\Gamma$ .

$\bullet$ Soit $f$ une fonction deux fois dérivable sur l’intervalle $I$ à valeurs réelles.
Il y a équivalence entre
$\ast$ $f$ est concave sur $I$
$\ast$ $f'$ est décroissante sur $I$
$\ast$ $f''$ est à valeurs négatives ou nulles
$\ast$ pour tout $a \in I$ , le graphe $\Gamma$ de $f$ est situé en dessous de la tangente en $(A , f(a))$ à la courbe $\Gamma$ .

Démonstration à connaître
Si la fonction $f''$ est positive ou nulle,
pour tout $a \in I$ , le graphe $\Gamma$ de $f$ est situé en dessous de la tangente en $(a , \,f(a))$ à la courbe $\Gamma$ .

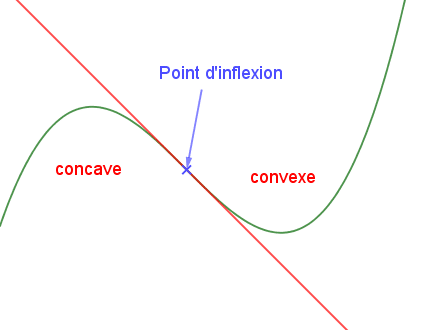
3.3. Point d’inflexion au programme de terminale

$\bullet$ Soit $f$ une fonction dérivable sur $I$ à valeurs dans $\mathbb{R}$ et $\Gamma$ son graphe.
Soit $a \in I$ et $A (a , \, f(a))$ est un point d’inflexion de $\Gamma$ lorsque la courbe traverse sa tangente en $A$ .
Ce qui est équivalent à $f$ change de concavité en $a$ .

Lorsque $f$ est deux fois dérivable,
$A(a , f(a))$ est un point d’inflexion ssi $f''$ s’annule en changeant de signe en $a$ .

3.4. Application à la démonstration d’inégalité

$\bullet$ En utilisant un raisonnement de convexité, on va montrer que
$\ast$ pour tout réel $x$ , $\textrm{e} ^x \geqslant 1 + x$
$\ast$ si $a, b$ sont réels, $\displaystyle \textrm{e} ^{(a + b)/2} \leqslant \frac{\textrm{e} ^a + \textrm{e} ^b} 2$ .

$\bullet$ La fonction $f : x \mapsto \textrm{e} ^x$ est convexe sur $\mathbb{R}$ car elle est deux fois dérivable et $f''(x) = f'(x) = \textrm{e} ^x \geqslant 0$
$f'(0) = 1$ .
La tangente en $(0 , f(0)) = (0 , 1)$ a pour équation $y = 1 + x$ .
La courbe est au dessus de sa tangente en $(0 , 1)$ : pour tout réel $x$ , $\textrm{e} ^x \geqslant 1 + x$

$\bullet$ On conserve la même fonction.
On considère les points $A(a , \textrm{e}^a )$ et $B(b , \textrm{e}^b)$
Le milieu $C$ de ce segment a pour coordonnées $\left ( \displaystyle \frac {a + b} 2 \, ,\, \frac{\textrm{e} ^a + \textrm{e} ^b} 2 \right)$ , il est situé au dessus du point d’abscisse $(a + b) / 2$ de $\Gamma$
donc $\displaystyle \textrm{e} ^{(a + b)/2} \leqslant \frac{\textrm{e} ^a + \textrm{e} ^b} 2$ .

$\bullet$ En utilisant un raisonnement de convexité, on va montrer que pour tout $x > - 1$ , $\sqrt{1 + x} \leqslant \displaystyle \frac x 2$ .

$\bullet$ La fonction $f : x \mapsto \sqrt{1 + x}$ est deux fois dérivable sur $]- 1 , + \infty[$
$f'(x) = \displaystyle \frac {1} {2 \sqrt{1 + x} }$
$f''(x) = \displaystyle \frac { - 1 } {4 \sqrt{1 + x} }. \frac 1 {1 + x}$
en posant $v(x) = 2 \sqrt{1 + x}$ et en utilisant $\left ( \displaystyle \frac 1 v \right ) ' =\displaystyle \frac {- v' } {v ^2}$ avec $v' : x \mapsto \displaystyle \frac 1 {4 \sqrt{1 + x}}$
$f''(x) = \displaystyle \frac {- 1} {4 \sqrt{1 + x} \, (1 + x) } < 0$
$f$ est concave.
$f'(0) = \displaystyle \frac 1 2$
La tangente en $(0 , f(0))$ a pour équation $y = 1 + \displaystyle \frac 1 2 x$ .
La courbe est située sous cette tangente donc $\sqrt{1 + x} \leqslant 1 + \displaystyle \frac 1 2 x\,$ .

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Avis Google France ★★★★★ 4,9 sur 5

N’hésitez pas à compléter ce cours en ligne avec des exercices d’annales de maths au bac afin de vous préparer au mieux à l’examen du bac. Vous avez également la possibilité de participer à des stages de révisions pendant les vacances scolaires. Avec son fort coefficient au bac, les maths sont à travailler très rigoureusement.

N’hésitez pas à prendre de l’avance sur le programme de Maths en commençant les révisions des chapitres suivants du programme grâce aux cours en ligne de maths gratuits, notamment :

Cours sur les dérivées et la convexité en Terminale Générale

1. Retour sur les cours de première

1.1. Définitions de fonctions sur les dérivées et la convexité

1.2. Interprétation des fonctions dérivées en Terminale Générale

1.3. La fonction dérivée et son utilisation

1.4. La fonction dérivée et son utilisation

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

2. Dérivées d’une fonction composée en Terminale Générale

2.1. Théorème de composition en terminale

2.2. Les dérivées à connaître en terminale

3. La convexité en Terminale Générale

3.1. Dérivée seconde

3.2. Fonction convexe et fonction concave

3.3. Point d’inflexion au programme de terminale

3.4. Application à la démonstration d’inégalité

PROF DE MATHS PARTICULIER

Des cours de qualité et enseignants aguerris

Préparer des concours ou s'exercer

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales