Chapitres Maths en Terminale Générale
Arithmétique : Exercices et corrigés en Terminale Générale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Exercice sur l’utilisation de la division euclidienne
Question 1 :
Déterminer la somme des multiples de ![]() compris entre
compris entre ![]() et
et ![]() .
.
Valeur ?
Question 2 :
Quel est le reste de la division euclidienne par ![]() de la somme de deux carrés de deux entiers relatifs consécutifs ?
de la somme de deux carrés de deux entiers relatifs consécutifs ?
Valeur du reste ?
Question 3 :
Résoudre dans ![]() ,
, ![]() divise
divise ![]() .
.
Nombre de solutions ?
Question 4 :
Résoudre dans ![]() ,
, ![]() divise
divise ![]() .
.
Nombre de solutions ?
Exercice sur l’utilisation de la relation de congruence
Question 1 :
Résoudre l’équation ![]() .
.
Question 2 :
En utilisant une congruence modulo 8, résoudre l’équation ![]() où
où ![]() et
et ![]() sont des entiers naturels.
sont des entiers naturels.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice sur la résolution d’équation dans 
Le but de l’exercice est de résoudre l’équation ![]() lorsque
lorsque ![]() .
.
Question 1 :
Résoudre l’équation lorsque ![]() .
.
Question 2 :
On suppose que ![]() et que
et que ![]() est solution.
est solution.
a) ![]() .
.
Vrai ou Faux ?
b) ![]() est un multiple de
est un multiple de ![]() .
.
Vrai ou Faux ?
c) Conclure en raisonnant modulo 5.
Exercice sur une suite arithmético-géométrique
On considère la suite définie par ![]() , et pour tout entier
, et pour tout entier ![]() ,
, ![]() .
.
Question 1 :
Si ![]() ,
, ![]() et
et ![]()
Vrai ou Faux ?
Question 2 :
Pour tout ![]() ,
, ![]() .
.
Vrai ou Faux ?
Exercice sur les nombres parfaits en Terminale
Écrire une fonction
![]() SommeDiviseurs
SommeDiviseurs
de paramètre ![]() qui calcule la somme des diviseurs de
qui calcule la somme des diviseurs de ![]() strictement inférieurs à
strictement inférieurs à ![]() .
.
Que donne SommeDiviseurs(2020) ?
![]() ?
?
Exercice pour coder et décoder un message
Question 1 :
Démontrer que si ![]() , alors
, alors ![]()
En déduire que 2 caractères distincts sont codés par 2 caractères distincts.
Question 2 :
Donner une fonction Python de paramètre un caractère qui donne la lettre obtenue par la transformation proposée.
Quelle est la lettre renvoyée par CodeLettre(‘S’) ?
Question 3 :
Donner une fonction DecodeLettre de paramètre une lettre codée et donne la valeur de la lettre initiale.
Quelle est la lettre renvoyée par DecodeLettre(‘T’) ?
Correction de l’exercice sur l’utilisation de la division euclidienne
Question 1 :
On cherche d’abord ![]() tel que
tel que
![]() .
.
or ![]()
et ![]()
donc ![]()
ssi ![]()
ssi ![]() .
.
On calcule donc 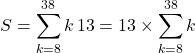
On additionne ![]() termes d’une suite arithmétique de premier terme
termes d’une suite arithmétique de premier terme ![]() et de dernier terme
et de dernier terme ![]() :
:
![]()
![]() .
.
Question 2 :
On raisonne par disjonction des cas.
![]() Dans le cas des entiers consécutifs :
Dans le cas des entiers consécutifs : ![]() et
et ![]() ,
,
![]()
![]() .
.
Le reste est égal à ![]() .
.
![]() Dans le cas des entiers consécutifs :
Dans le cas des entiers consécutifs : ![]() et
et ![]() ,
,
![]()
![]()
![]() .
.
Le reste est égal à ![]() .
.
Dans les deux cas, le reste est égal à 1.
Question 3 :
Si ![]() divise
divise ![]() , alors
, alors ![]() divise
divise ![]() donc
donc ![]() .
.
On étudie la réciproque.
Si ![]() ,
,
![]() divise 4 donc
divise 4 donc ![]() divise
divise ![]() .
.
![]()
ssi ![]() .
.
L’ensemble des solutions est ![]() .
.
Question 4 :
![]()
![]()
![]() .
.
Comme ![]() divise
divise ![]() et
et ![]() , alors
, alors ![]() divise 24 donc
divise 24 donc ![]() est élément de
est élément de
![]() .
.
On étudie la réciproque.
Si ![]() est élément de
est élément de ![]() ,
,
![]() divise 24, donc
divise 24, donc ![]() divise
divise ![]()
et ![]() divise
divise ![]()
Puis il reste à traduire ![]() est élément de
est élément de ![]() ,
,
ce qui donne l’ensemble ![]() des solutions
des solutions
![]()
![]() .
.
Correction d’exercice sur l’utilisation de la relation de congruence
Question 1 :
Si ![]() ,
, ![]() .
.
On étudie le cas où ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
donc si ![]() ,
, ![]() ssi
ssi ![]()
alors si ![]() ,
, ![]() ssi
ssi ![]() .
.
L’ensemble des solutions est l’ensemble des entiers ![]() .
.
Question 2 :
![]()
![]() ,
, ![]()
donc ![]()
et ![]()
![]() On suppose qu’il existe une solution avec
On suppose qu’il existe une solution avec ![]() , alors
, alors ![]()
donc
![]() et
et ![]()
impliquent que ![]()
soit ![]() ou
ou ![]()
ce qui contredit le fait que ![]() est congru à 3 ou 1 modulo 8.
est congru à 3 ou 1 modulo 8.
Il est impossible que ![]() .
.
![]() Si
Si ![]() ,
,
![]() ssi
ssi ![]() ssi
ssi ![]() , ce qui est impossible
, ce qui est impossible
![]() Si
Si ![]() ,
,
![]() ssi
ssi ![]() ssi
ssi ![]() , ssi
, ssi ![]() .
.
![]() Si
Si ![]() ,
,
![]() ssi
ssi ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
Les couples solutions sont ![]() et
et ![]()
Correction d’exercice sur la résolution d’équation dans 
Question 1 :
On note ![]() et on raisonne par disjonction des cas.
et on raisonne par disjonction des cas.
![]() Si
Si ![]() ,
,
![]() car égal à
car égal à ![]() ou au moins égal à
ou au moins égal à ![]() .
.
![]() Si
Si ![]() ,
,
![]() ssi
ssi ![]() .
.
![]() Si
Si ![]() ,
,
![]() car égal à
car égal à ![]() ou
ou ![]() ou au moins égal à
ou au moins égal à ![]() .
.
![]() Si
Si ![]() ,
,
![]() car égal à
car égal à ![]() ou
ou ![]() ou au moins égal à
ou au moins égal à ![]() .
.
![]() Si
Si ![]() ,
,
![]() ssi
ssi ![]() .
.
Il y a deux couples solutions si l’on impose ![]() :
: ![]() .
.
Question 2 :
a) Vrai
![]() ,
,
Si ![]() ,
, ![]()
et comme ![]() alors
alors ![]() .
.
b) Vrai
![]() ,
, ![]() ,
, ![]() ,
, ![]()
car ![]() .
.
puis ![]()
car ![]() .
.
Soit ![]() ,
,
![]()
![]()
![]()
![]()
Donc ![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
c) Si ![]() est solution avec
est solution avec ![]() ,
, ![]() avec
avec ![]() .
.
![]() ,
, ![]()
donc ![]()
donc ![]() implique que
implique que ![]()
soit ![]() , donc
, donc ![]() divise
divise ![]() ce qui est impossible .
ce qui est impossible .
Il n’y a pas de solution avec ![]() .
.
Le problème proposé admet donc deux solutions ![]() et
et ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur une suite arithmético-géométrique
Question 1 :
Vrai
Si ![]() , on note
, on note
![]() :
: ![]() et
et ![]()
![]() Initialisation.
Initialisation.
![]() et
et ![]() , donc
, donc ![]() est vraie.
est vraie.
![]() Hérédité.
Hérédité.
On suppose que ![]() est vraie pour un entier
est vraie pour un entier ![]() donné.
donné.
On rappelle que ![]() ,
,
alors ![]()
donc ![]()
et ![]()
donc ![]() .
.
On a prouvé ![]() .
.
![]() Conclusion.
Conclusion.
Par récurrence, la propriété est vraie pour tout entier ![]() .
.
On gagne un peu de temps en incluant les deux équivalences dans la même hypothèse de récurrence.
Question 2 :
Vrai
Si ![]() , on note
, on note
![]() :
: ![]()
![]() Initialisation.
Initialisation.
![]() donc
donc ![]() est vraie.
est vraie.
![]() Hérédité.
Hérédité.
On suppose que ![]() est vraie pour un entier
est vraie pour un entier ![]() donné.
donné.
![]()
![]()
![]() .
.
On a prouvé ![]() .
.
![]() Conclusion.
Conclusion.
Par récurrence, la propriété est vraie pour tout entier ![]() .
.
Correction de l’exercice sur les nombres parfaits en Terminale
![]()
def SommeDiviseurs(n):
![]() S = 1
S = 1
![]() for k in range(2 , n):
for k in range(2 , n):
![]() if n % k
if n % k ![]() :
:
![]() S = S + k
S = S + k
![]() return(S)
return(S)
SommeDiviseurs(2020)
![]() .
.
Correction de l’exercice pour coder et décoder un message
Question 1 :
![]() On suppose que
On suppose que ![]() alors
alors ![]()
et ![]()
or ![]() , donc
, donc ![]()
et ![]() , donc
, donc ![]() .
.
On a prouvé que ![]() .
.
![]() Si
Si ![]() (resp
(resp ![]() ) est le numéro du code de la lettre numéro
) est le numéro du code de la lettre numéro ![]() (resp.
(resp. ![]() ), alors
), alors ![]() avec
avec ![]() et
et ![]()
donc ![]()
![]() et
et ![]()
donc ![]() et comme
et comme ![]() , alors
, alors ![]() .
.
Question 2 :
def CodeLettre (L) :
![]() x = numero(L)
x = numero(L)
![]() y = (5*x + 4) % 27
y = (5*x + 4) % 27
![]() return (alphabet[y] )
return (alphabet[y] )
On pourrait bien sûr écrire seulement
def CodeLettre (L) :
![]() y = (5* numero(L) + 4) % 27
y = (5* numero(L) + 4) % 27
![]() return ( alphabet[y])
return ( alphabet[y])
CodeLettre(‘S’)
réponse ‘N’
Question 3 :
def DecodeLettre(L):
![]() y = numero (L)
y = numero (L)
![]() x = (11*y + 10) % 27
x = (11*y + 10) % 27
![]() return (alphabet[x])
return (alphabet[x])
On pourrait se limiter aussi à
def DecodeLettre(L):
![]() x = (11* numero(L) + 10) % 27
x = (11* numero(L) + 10) % 27
![]() return (alphabet[x])
return (alphabet[x])
DecodeLettre(« T »)
réponse ‘D’.
N’hésitez pas à vous servir des autres cours en ligne de maths au programme de l’option maths expertes pour vous préparer à l’examen du bac. Vous pourrez y retrouver des définitions, des propriétés, des exemples, des conseils, des méthodes….
Retrouvez ici les chapitres à connaître en spé maths expertes :

