Chapitres Maths en Terminale Générale
Exercices la chaîne de Markov en terminale et corrigés gratuits
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Exercice 1 – Sujet de bac
Dans une société d’assurance, les clients peuvent choisir de payer leur cotisation chaque mois (paiement mensuel) ou en une fois (paiement annuel).
On constate que ![]() de ceux qui paient en une fois choisissent le paiement mensuel l’année suivante, alors que
de ceux qui paient en une fois choisissent le paiement mensuel l’année suivante, alors que ![]() de ceux qui paient chaque mois conservent ce mode de paiement l’année suivante.
de ceux qui paient chaque mois conservent ce mode de paiement l’année suivante.
En 2014, ![]() des clients paient en une fois et
des clients paient en une fois et ![]() paient mensuellement.
paient mensuellement.
Dans toute la suite de l’exercice, ![]() désigne un nombre entier naturel.
désigne un nombre entier naturel.
On note :
![]()
![]() la probabilité qu’un client choisi au hasard paie en une fois pour l’année
la probabilité qu’un client choisi au hasard paie en une fois pour l’année ![]() ;
;
![]()
![]() la probabilité qu’un client choisi au hasard paie mensuellement pour l’année
la probabilité qu’un client choisi au hasard paie mensuellement pour l’année ![]() .
.
On a ![]() et
et ![]() et on note
et on note ![]() l’état probabiliste pour l’année
l’état probabiliste pour l’année ![]() . Ainsi
. Ainsi ![]() .
.
On note :
![]()
![]() l’état « le client paie en une fois » ;
l’état « le client paie en une fois » ;
![]()
![]() l’état « le client paie mensuellement ».
l’état « le client paie mensuellement ».
Question 1 :
Représenter un graphe probabiliste de sommets ![]() et
et ![]() .
.
Question 2 :
Écrire la matrice de transition ![]() associée à ce graphe en prenant les sommets dans l’ordre alphabétique.
associée à ce graphe en prenant les sommets dans l’ordre alphabétique.
Question 3 :
Déterminer la probabilité qu’un client paie en une fois durant l’année 2018 (arrondir le résultat au millième).
Question 4 :
Déterminer la distribution invariante et en donner une interprétation.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 sur la chaîne de Markov en Terminale
Un lapin se déplace dans un terrier composé de trois galeries, notées A, B et C, dans chacune desquelles il est confronté à un stimulus particulier.
À chaque fois qu’il est soumis à un stimulus, le lapin reste dans la galerie où il se trouve ou change de galerie. Cela constitue une étape.
S’il est dans la galerie ![]() ou
ou ![]() , il y reste avec la probabilité
, il y reste avec la probabilité ![]() ou il passe dans la galerie
ou il passe dans la galerie ![]() avec la probabilité
avec la probabilité ![]()
S’il est dans la galerie ![]() , il y reste avec la probabilité
, il y reste avec la probabilité ![]() sinon il passe dans la galerie
sinon il passe dans la galerie ![]() ou la galerie
ou la galerie ![]() avec la probabilité
avec la probabilité ![]() .
.
Question 1 :
Représenter le graphe de probabilité associé à cette situation.
On notera ![]() ,
, ![]() et
et ![]() les trois états correspondant aux trois galeries.
les trois états correspondant aux trois galeries.
Question 2 :
Écrire la matrice de transition associée.
Question 3 :
Écrire en justifiant le raisonnement la relation liant ![]() ,
, ![]() et
et ![]() .
.
Question 4 :
Déterminer la distribution stationnaire.
On donnera les trois valeurs sans parenthèses, sous la forme ![]() en les séparant par une virgule.
en les séparant par une virgule.
Question 5 :
On définit la suite ![]() par
par
![]() si
si ![]() ,
, ![]() .
.
a) La suite ![]() est géométrique de raison :
est géométrique de raison :
b) Pour tout ![]() ,
, ![]() .
.
Exercice 3 de Terminale Générale sur la chaîne de Markov
Le PageRank ou PR est l’algorithme d’analyse des liens concourant au système de classement des pages Web utilisé par le moteur de recherche Google.
Il mesure quantitativement la popularité d’une page web. Le PageRank n’est qu’un indicateur parmi d’autres dans l’algorithme qui permet de classer les pages du Web dans les résultats de recherche de Google.
Ce système a été inventé par Larry Page, cofondateur de Google.
On en examine une illustration sur un nombre faible de pages
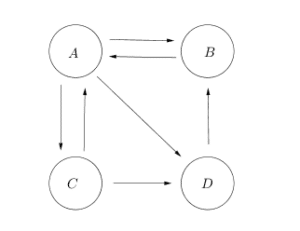
On considère 4 pages notées ![]() et
et ![]() .
.
Les flèches indiquent les hyperliens menant d’une page à une autre.
On choisit une page au hasard , pour chaque page sur laquelle on arrive, on choisit une page au hasard etc …
Question 1 :
Écrire une fonction Python nommée choix et de paramètre PagePrec qui choisit la page suivante au hasard sur les pages disponibles.
En chargeant le module random l’appel à
![]() random.choice(L)
random.choice(L)
choisit au hasard un des éléments de la liste ![]() .
.
Question 2 :
Écrire une deuxième fonction Python de paramètres ![]() et
et ![]() qui, partant de la page
qui, partant de la page ![]() effectue
effectue ![]() clics et renvoie le numéro de la page d’arrivée.
clics et renvoie le numéro de la page d’arrivée.
Question 3 :
Écrire une fonction Python TestPages , de paramètre le nombre de clics, qui choisit au hasard la première page et qui renvoie la liste du nombre de visites pour chaque page.
random.randint(a , b) donne un entier choisi au hasard entre l’entier ![]() et l’entier
et l’entier ![]() .
.
Question 4 :
Définir une fonction Maximum de paramètre une liste ![]() et qui renvoie la liste [indice,valeur], où valeur est la valeur maximale de la liste
et qui renvoie la liste [indice,valeur], où valeur est la valeur maximale de la liste ![]() et indice , le premier indice pour lequel on rencontre ce maximum.
et indice , le premier indice pour lequel on rencontre ce maximum.
La vérifier avec ![]()
Question 5 :
Écrire une fonction qui permette de tester la meilleure page pour un nombre de clics élevé :
Pour les 4 pages initiales possibles, on effectue nbClics et déterminer la page la plus visitée et le nombre de visites.
On pourra la tester pour 1000 clics.
Correction exercice 1 du sujet de bac sur la chaîne de Markov
Question 1 :
L’énoncé donne :
L’assurance payée annuellement l’est encore l’année suivante avec la probabilité ![]() et payée mensuellement avec la probabilité
et payée mensuellement avec la probabilité ![]() .
.
L’assurance payée mensuellement l’est encore l’année suivante avec la probabilité ![]() et payée annuellement avec la probabilité
et payée annuellement avec la probabilité ![]() .
.
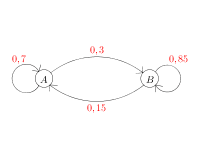
ce qui donne le graphe probabiliste pour les deux états ![]() et
et ![]() :
:
Question 2 :
Si ![]() (resp.
(resp. ![]() ) est l’événement le client paye en une seule fois (resp. mensuellement) pour l’année
) est l’événement le client paye en une seule fois (resp. mensuellement) pour l’année ![]() )
)
l’énoncé donne pour tout entier ![]() ,
,
![]() ,
, ![]()
![]()
et ![]()
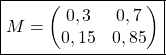 .
.
Question 3 :
On rappelle la démonstration :
Par la formule des probabilités totales,
![]()
![]()
soit ![]()
et ![]()
![]()
soit ![]()
ce qui se traduit par ![]() .
.
donc ![]() avec
avec ![]() et
et ![]()
et en arrondissant les résultats au millième, ![]() .
.
La probabilité qu’un client paie en une fois durant l’année 2018 est égale à ![]() .
.
Question 4 :
On détermine ![]() et
et ![]() tels que
tels que ![]()
soit ![]()
ssi ![]()
ssi ![]()
ssi ![]() ssi
ssi ![]()
Comme on veut que ![]() , on doit avoir
, on doit avoir ![]() ssi
ssi ![]()
La distribution invariante est donnée par 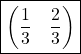 .
.
On peut donc estimer que pour ![]() grand, la probabilité de payer annuellement sera proche de
grand, la probabilité de payer annuellement sera proche de ![]() et celle de payer mensuellement sera proche de
et celle de payer mensuellement sera proche de ![]() .
.
Correction exercice 2 de la chaîne de Markov
Question 1 :
L’énoncé donne
S’il est dans ![]() (resp.
(resp. ![]() ), il y reste avec la probabilité
), il y reste avec la probabilité ![]() et il passe dans
et il passe dans ![]() avec la probabilité
avec la probabilité ![]() .
.
S’il est dans ![]() , il y reste avec la probabilité
, il y reste avec la probabilité ![]() et il passe dans
et il passe dans ![]() (resp.
(resp. ![]() ) avec la probabilité
) avec la probabilité ![]()
Ce qui donne le graphe de probabilité à trois états ![]() ,
,![]() et
et ![]() :
:
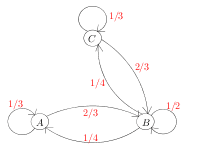
Question 2 :
On traduit les données de l’énoncé par :
![]()
![]()
alors ![]()
![]()
![]()
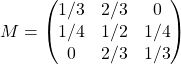
Question 3 :
On fixe ![]() .
.
La famille ![]() est un système complet d’événements.
est un système complet d’événements.
Par la formule des probabilités totales,
![]()
![]()
![]()
soit ![]()
de même ![]() .
.
![]()
![]()
![]()
donc ![]()
soit pour tout ![]() ,
, ![]() .
.
Question 4 :
On cherche ![]() tel que
tel que ![]()
![]() et
et ![]() étant positifs ou nuls et de somme égale à 1.
étant positifs ou nuls et de somme égale à 1.
Comme tous les éléments de ![]() sont strictement positifs, on sait que
sont strictement positifs, on sait que ![]() existe et est unique.
existe et est unique.
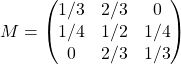
![]() ssi
ssi ![]()
ssi 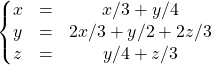
ssi 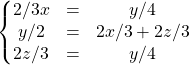
ssi 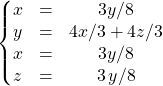
ssi ![]() car alors
car alors ![]()
On a obtenu ![]() .
.
La somme des éléments est égale à ![]() ssi
ssi ![]()
donc 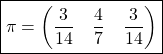 .
.
Question 5 :
a) ![]()
![]()
donc ![]() .
.
![]() est une suite géométrique de raison
est une suite géométrique de raison ![]() .
.
b) Par propriété des suites géométriques, pour tout ![]() ,
,
![]() .
.
sachant que ![]() et
et ![]() , alors
, alors ![]() soit
soit ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction exercice 3 de terminale sur la chaîne de Markov
Question 1 :
On numérote les pages de ![]() à
à ![]() .
.
Si l’on est sur la page ![]() , on choisit une page parmi
, on choisit une page parmi ![]() .
.
Si l’on est sur la page ![]() , on choisit une page parmi
, on choisit une page parmi ![]() .
.
Si l’on est sur la page ![]() (resp 3), on passe sur la page 0 (resp. 1).
(resp 3), on passe sur la page 0 (resp. 1).
def choix(PagePrec):
![]() if PagePrec == 0:
if PagePrec == 0:
![]() R = random.choice ([1, 2, 3])
R = random.choice ([1, 2, 3])
![]() elif PagePrec == 1:
elif PagePrec == 1:
![]() R = 0
R = 0
![]() elif PagePrec == 2:
elif PagePrec == 2:
![]() R = random.choice([0, 3])
R = random.choice([0, 3])
![]() else :
else :
![]() R = 1
R = 1
![]() return R
return R
Question 2 :
def Partant(k,n):
![]() page = k
page = k
![]() for i in range(n):
for i in range(n):
![]() page = choix(page)
page = choix(page)
![]() return page
return page
Question 3 :
On définit une liste ![]() formée de
formée de ![]() zéros.
zéros.
Quand on arrive sur une page, il suffit d’augmenter L[page ] d’une unité pour marquer qu’elle a été visitée une fois de plus.
def TestPages (nbClics):
![]() L = [0 for k in range(4)]
L = [0 for k in range(4)]
![]() Page = random.randint(0,3)
Page = random.randint(0,3)
![]() L[Page] = 1
L[Page] = 1
![]() for essai in range(nbClics):
for essai in range(nbClics):
![]() Page = choix(Page)
Page = choix(Page)
![]() L[Page]= L[Page]+ 1
L[Page]= L[Page]+ 1
![]() return (L)
return (L)
![]() TestPages(1000)
TestPages(1000)
[377, 303, 136, 185]
Question 4 :
def Maximum(L):
![]() n = len(L)
n = len(L)
![]() maxi = L[0]
maxi = L[0]
![]() indice = 0
indice = 0
![]() for i in range(1, n):
for i in range(1, n):
![]() if L[i]> maxi :
if L[i]> maxi :
![]() indice = i
indice = i
![]() maxi = L[i]
maxi = L[i]
![]() return [indice,maxi]
return [indice,maxi]
explication : on détermine le nombre d’éléments de la liste.
On initialise maxi par L[0] et indice par 0.
Puis on décrit la liste, en modifiant les variables maxi et indice lorsque l’on obtient une valeur ![]() strictement supérieure au maxi provisoire.
strictement supérieure au maxi provisoire.
![]() Maximum([4,3,2,1,7,6,7,3])
Maximum([4,3,2,1,7,6,7,3])
[4, 7]
Question 5 :
def TestMeilleurePage (nbClics):
![]() L = [0 for k in range(4)]
L = [0 for k in range(4)]
![]() for k in range (4):
for k in range (4):
![]() Lk = [0 for i in range(4)]
Lk = [0 for i in range(4)]
![]() Page = k
Page = k
![]() Lk[k] = 1
Lk[k] = 1
![]() for essai in range(nbClics):
for essai in range(nbClics):
![]() Page = choix(Page)
Page = choix(Page)
![]() Lk[Page]= Lk[Page] + 1
Lk[Page]= Lk[Page] + 1
![]() L[k] = Maximum(Lk)
L[k] = Maximum(Lk)
![]() return (L)
return (L)
![]() TestMeilleurePage(1000)
TestMeilleurePage(1000)
[[0, 378], [0, 378], [0, 373], [0, 368]]
La page la plus visitée est la page ![]() donc nommée
donc nommée ![]() , indépendamment de la page de départ.
, indépendamment de la page de départ.
Pour vous préparer à l’examen du bac, retrouvez des définitions, des exemples, conseils et méthodes sur les autres chapitres du programme de l’option maths expertes.
Retrouvez ici les chapitres à connaître en spé maths expertes :

