Chapitres Maths en Terminale Générale
Complexes en Terminale générale : exercices corrigés
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Ces exercices en ligne aide à saisir les bases des complexes au programme de Maths de Terminale. En plus de cela, travailler sur des annales de bac de Maths peut vous aider à vous mettre en conditions réelles. Si malgré cela vous souffrez encore de grosses difficultés, des cours particuliers de maths sauront vous remettre rapidement à niveau.
Résolutions d’équations sur les nombres complexes en Terminale
Première équation :
Résoudre dans ![]() :
: ![]() .
.
Deuxième équation
Trouver ![]() tel que
tel que ![]() .
.
Troisième équation
Résoudre dans ![]() l’équation
l’équation
![]() .
.
Extrait d’annales de bac sur les complexes : Antilles 2003
Le plan est rapporté au repère orthonormal ![]()
(unité graphique : 2 cm).
On considère les points ![]() et
et ![]() d’affixes respectives
d’affixes respectives ![]() et
et ![]() .
.
Extérieurement au triangle ![]() , on construit les deux carrés
, on construit les deux carrés ![]() et
et ![]() .
.
Pour tous ces points, on notera l’affixe par la minuscule correspondante.
Question 1
a. Déterminer ![]() et en utilisant
et en utilisant ![]() , déterminer
, déterminer
l’affixe ![]() de
de ![]() . En déduire l’affixe
. En déduire l’affixe ![]() du centre
du centre ![]() du carré
du carré ![]() .
.
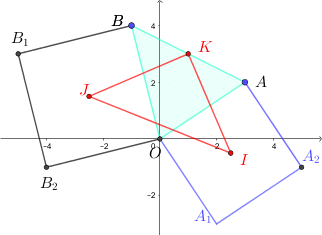
b. En raisonnant de même déterminer l’affixe ![]() de
de ![]() . En déduire l’affixe
. En déduire l’affixe ![]() du centre
du centre ![]() du carré
du carré ![]() .
.
Question 2
Calculer l’affixe ![]() du milieu
du milieu ![]() du segment
du segment ![]() . À l’aide des affixes des différents points, calculer les valeurs des longueurs
. À l’aide des affixes des différents points, calculer les valeurs des longueurs ![]() et
et ![]() , ainsi qu’une mesure de l’angle
, ainsi qu’une mesure de l’angle ![]() .
.
Que peut-on en déduire?
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Les suites de Mandelbrot en Terminale
On appelle suite de Mandelbrot toute suite complexe ![]() définie par
définie par ![]() 0 et pour tout
0 et pour tout ![]() où
où ![]() .
.
On démontre qu’il n’y a que deux cas :
![]() la suite
la suite ![]() est bornée.
est bornée.
![]() la suite
la suite ![]() n’est pas bornée, ce qui est équivalent à
n’est pas bornée, ce qui est équivalent à ![]() .
.
On appelle ensemble de Mandelbrot l’ensemble des complexes ![]() tels que la suite de Mandelbrot associée soit bornée.
tels que la suite de Mandelbrot associée soit bornée.
La représentation dans le plan complexe des points de ![]() est donnée par l’image illustrant ce chapitre.
est donnée par l’image illustrant ce chapitre.
C’est un ensemble fractal très célèbre.
Question 1
![]() ,
, ![]() ,
, ![]() sont des points de
sont des points de ![]() ,
, ![]() .
.
Vrai ou Faux ?
Question 2
La représentation dans le plan complexe de ![]() est symétrique par rapport à l’axe des réels.
est symétrique par rapport à l’axe des réels.
Vrai ou Faux ?
Question 3
Si ![]() et
et ![]() sont complexes,
sont complexes, ![]() .
.
Vrai ou Faux ?
Correction des équations sur les nombres complexes en Terminale
Correction de la Première équation
L’équation ![]() admet
admet ![]() pour racine évidente, le produit des racines est
pour racine évidente, le produit des racines est ![]() donc l’autre racine est
donc l’autre racine est ![]() .
.
Il reste à résoudre ![]() puis
puis ![]() .
.
![]()
![]() ssi
ssi ![]() est racine cubique de
est racine cubique de ![]() ssi
ssi ![]() .
.
![]()
![]() ssi
ssi ![]() ssi
ssi ![]() est racine cubique de
est racine cubique de ![]() ssi
ssi ![]()
L’ensemble des solutions est :
![]()
donc 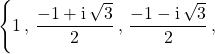
![]() .
.
Correction de la Deuxième équation
![]() .
.
On cherche ![]() vérifiant
vérifiant ![]() sous la forme
sous la forme ![]() avec
avec ![]() solution du système :
solution du système :
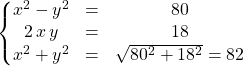
ssi 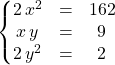
ssi ![]() ,
, ![]() et
et ![]() .
.
alors ![]() vérifie
vérifie ![]() .
.
Correction de la Troisième équation
![]() On pose
On pose ![]() et on résout l’équation du second degré
et on résout l’équation du second degré ![]()
dont le discriminant est :
![]()
![]()
![]() .
.
Les racines de cette équation du second degré sont ![]() et
et ![]() .
.
![]() On résout
On résout ![]() ssi
ssi ![]() ssi
ssi ![]()
avec ![]() et
et ![]() .
.
![]() On résout
On résout ![]()
![]()
![]()
![]() avec
avec ![]() .
.
On doit donc résoudre ![]()
ssi ![]()
ssi ![]() .
.
On rappelle que
![]()
![]() .
.
Les 6 racines de l’équation sont
![]()
![]()
![]()
soit aussi
![]()
et ![]() ,
, ![]() et
et ![]() .
.
Correction de l’extrait d’annales de bac sur les complexes
Correction de la question 1
a. ![]()
ce qui se traduit par
![]()
Soit ![]() .
.
Si l’on note ![]() , on a démontré que
, on a démontré que ![]() .
.
Puis ![]() soit
soit ![]() .
.
![]() est un complexe de module 1 et d’argument
est un complexe de module 1 et d’argument ![]() , donc
, donc ![]()
ce qui donne ![]()
![]() .
.
![]() est le milieu du segment
est le milieu du segment ![]() , donc
, donc ![]()
b. ![]()
ce qui se traduit par
![]() .
.
Soit ![]() .
.
Si l’on note ![]() , on a démontré que
, on a démontré que ![]() .
.
Puis ![]() ,
, ![]() .
.
![]() est un complexe de module 1 et d’argument
est un complexe de module 1 et d’argument ![]() , donc
, donc ![]() ,
,
ce qui donne ![]() .
.
![]() est le milieu du segment
est le milieu du segment ![]() , donc
, donc ![]() .
.
Correction de la question 2
![]() .
.
On détermine les affixes ![]() et
et ![]() de
de ![]() et
et ![]() :
:
![]()
![]() .
.
![]()
![]()
donc ![]() .
.
Ce qui donne ![]()
soit ![]() .
.
et ![]()
soit ![]()
soit aussi ![]() .
.
Donc ![]() .
.
Le triangle ![]() est rectangle isocèle en
est rectangle isocèle en ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction des suites de Mandelbot
Correction de la question 1
Vrai :
![]() Si
Si ![]() 0 , la suite
0 , la suite ![]() est une suite constante égale à 0.
est une suite constante égale à 0.
donc ![]() .
.
![]() Si
Si ![]() ,
,
pour tout ![]() ,
, ![]() .
.
![]() ,
, ![]()
alors ![]() et
et ![]() .
.
La suite ![]() est bornée.
est bornée. ![]()
![]() Si
Si ![]() ,
,
pour tout ![]() ,
, ![]() .
.
![]() ,
, ![]()
![]()
![]()
d’où si ![]() ,
, ![]() et
et ![]() .
.
La suite ![]() est bornée.
est bornée. ![]()
![]() Si
Si ![]() ,
,
pour tout ![]() ,
, ![]() .
.
On note si ![]() .
.
Initialisation
![]() donc
donc ![]() est vraie.
est vraie.
Hérédité
On suppose que ![]() est vraie.
est vraie.
Alors ![]() est un réel tel que
est un réel tel que
![]()
donc ![]() est vraie.
est vraie.
Conclusion
La propriété est vraie par récurrence.
Alors la suite ![]() n’est pas bornée, donc
n’est pas bornée, donc ![]() .
.
Correction de la question 2
Vrai :
Soit ![]() , on note
, on note ![]() la suite de Mandelbrot définie par le complexe
la suite de Mandelbrot définie par le complexe ![]() et
et ![]() celle définie à partir du complexe
celle définie à partir du complexe ![]() .
.
Si ![]() , on note
, on note ![]() .
.
Initialisation
![]() donc
donc ![]() est vraie.
est vraie.
Hérédité
On suppose que ![]() est vraie.
est vraie.
Alors ![]()
![]() .
.
Donc ![]() est vraie.
est vraie.
Conclusion
La propriété est vraie par récurrence.
Alors pour tout ![]() .
.
La suite ![]() est bornée ssi
est bornée ssi ![]() est bornée.
est bornée.
Donc ![]() ssi
ssi ![]() .
.
La représentation de ![]() est symétrique par rapport à l’axe des réels.
est symétrique par rapport à l’axe des réels.
Correction de la question 3
Vrai
![]()
donne par inégalité triangulaire :
![]()
soit ![]()
donc ![]() .
.
La spécialité maths a un coefficient au Bac très élevé, comme vous pouvez le voir sur notre simulateur du bac. Il est donc essentiel de la travailler au maximum, de même que votre deuxième spécialité. C’est indispensable si vous voulez être entièrement satisfait au moment des résultats du Bac. Tous les chapitres suivants devront être parfaitement assimilés pour réussir l’épreuve maths lors du bac :

