Chapitres Maths en Terminale Générale

Exercices et corrigés de maths sur la continuité en Terminale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Entraînez-vous et préparez-vous pour le bac à l’aide des exercices ci-dessous sur la continuité au programme de maths en Terminale. Il est nécessaire pour l’élève de Terminale d’avoir parfaitement assimilé les cours de maths au programme de maths en 1ère, car les chapitres abordés lors du programme de Terminale s’inscrivent dans la continuité de ceux de la classe de 1ère. Les élèves ont donc tout intérêt à travailler très sérieusement dès le début du lycée, d’autant plus que le coefficient au bac de l’épreuve de maths est relativement élevé.

1. Étude de continuité en Terminale

Exercice 1 sur la continuité en Terminale

Question 1 :
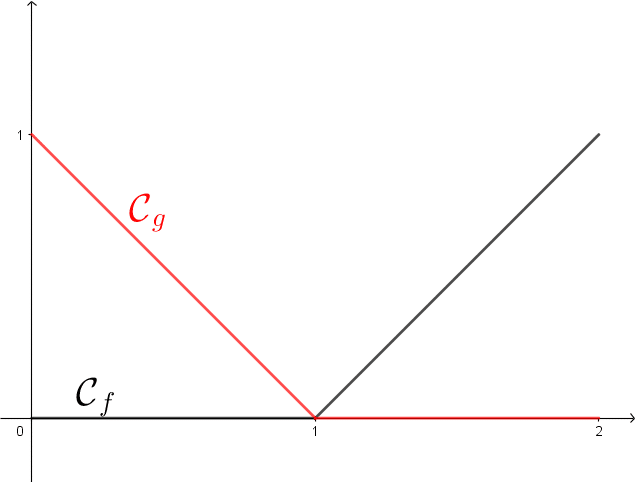
Étudier la continuité et tracer le graphe de la fonction $f$ définie par
$\qquad$ si $x\in [0, 1]$ , $f(x) = 0$
$\qquad$ et si $x \in\; ]1 , 2]$ , $f(x) = x- 1$ .
$f$ est continue Vrai ou Faux ?

Question 2 :
Étudier la continuité et tracer le graphe de la fonction $g$ définie par
$\qquad$ si $x\in [0, 1]$ , $g(x) = 1-x$
$\qquad$ et si $x \in \; ]1 , 2]$ , $g(x) = 0$ .
$g$ est continue Vrai ou Faux ?

Question 3 :
La fonction nulle sur $[0 , 2]$ est le produit de deux fonctions continues sur $[0 , 2]$ et différentes de la fonction nulle.
Vrai ou Faux ?

Correction de l’exercice 1 sur la continuité en Terminale

Question 1 :
$f$ est continue Vrai ou Faux ? Vrai

$\bullet$ $f$ est continue sur $[0 , 1[$ et sur $]1 , 2]$ .

$\bullet$ $\displaystyle \lim_{x \to 1 ^{- }} f(x) = 0$ , $\displaystyle \lim_{x \to 1 ^{+ }} f(x) = 1-1 = 0$
et $f(1) = 0$ , donc $f$ est continue en $1$ .

Conclusion : $f$ est continue sur $[0 , 2]$ .

Question 2 :
$g$ est continue Vrai ou Faux ? Vrai

$\bullet$ $g$ est continue sur $[0 , 1[$ et sur $]1 , 2]$ .

$\bullet$ $\displaystyle \lim_{x \to 1 ^{- }} g(x) = 1 - 1 = 0$ , $\displaystyle \lim_{x \to 1 ^{+ }}g(x) = 0$
et $g(1) = 0$ , donc $g$ est continue en $1$ .

Conclusion : $g$ est continue sur $[0 , 2]$ .

Question 3 :
Vrai ou Faux ? Vrai

Pour $x\in [0, 1[, \, (f g)(x) = f(x) g(x) = 0$ car $f(x) = 0$
Pour $x \in [1 , 2],\, (f g)(x) = f(x) g(x) = 0$ car $g(x) = 0$
donc $f g$ est la fonction nulle et les deux fonctions continues $f$ et $g$ ne sont pas des fonctions nulles.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

2. Sur la partie entière, chapitre de continuité en Terminale

Exercice sur la partie entière en continuité

On définit la fonction $f$ partie entière sur $\mathbb{R}$ par
$f(x) = n$ si $x \in [n , n + 1[$ où $n \in \mathbb{Z}$ .
On note encore $f(x) = \lfloor x \rfloor$

Question 1 :
La fonction partie entière est continue en tout réel $a$ non entier et discontinue en $a \in \mathbb{Z}$ .
Vrai ou Faux ?

Question 2 :
On définit pour $x \in \mathbb {R}$ , par $\qquad g(x) = \lfloor x \rfloor + (x - \lfloor x \rfloor) ^2$ .
Étudier la continuité de $g$ .
$g$ est discontinue, Vrai ou Faux ?

Question 3 :
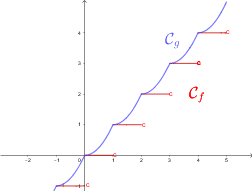
Représenter les fonctions $f$ et $g$ sur $[-1, 5]$ dans le même repère.

Correction de l’exercice sur la partie entière en continuité

Question 1 :
Vrai ou Faux ? Vrai

$\bullet$ Pour tout $n \in \mathbb{Z}$ ,
si $x \in \; ]n , n + 1[, \lfloor x \rfloor = n$ .
La fonction partie entière est constante donc continue sur $]n , n + 1[$ .

$\bullet$ Étude de la continuité en $n \in \mathbb{Z}$
$\ast$ $\displaystyle \lim_{x \to n ^{+}} \lfloor x \rfloor = n = \lfloor n \rfloor = f(n)$
$f$ est continue à droite en $n$ .

$\ast$ Si $x \in \; ] n - 1 , n [ ,\, \lfloor x \rfloor = n - 1$
donc $\displaystyle \lim_{x \to n ^{-}} \lfloor x \rfloor = n - 1 \neq \lfloor n \rfloor$ .
$f$ n’est pas continue à gauche en $n$ .

Question 2 :
$g$ est discontinue ? Faux

Si $x \in [n , n + 1[$ où $n \in \mathbb{Z}$ ,
$\qquad \quad g(x) = n + (x - n)^2$
alors $g$ est continue sur $]n , n + 1[$ car c’est une fonction polynôme
et $\displaystyle \lim_{x \to n ^{ +}} g(x) = n + 0 = n = g(n)$ .

Sur $]n - 1 , n [$ , $\qquad g(x) = n - 1 + (x - n + 1)^2$
donc $\displaystyle \lim_{x \to n ^{ -}} g(x) = n - 1 + 1 = n = g(n)$ .

$g$ est continue à droite et à gauche en $n$ , donc $g$ est continue en $n$ .
$g$ est continue sur $\mathbb{R}$ .

On remarque ici qu’une fonction s’exprimant à l’aide d’une fonction discontinue peut être continue.

Question 3 :

3. Résolution d’équations

Exercice sur la résolution d’équations en continuité en Terminale

Question 1 :
Étudier les variations de $\qquad \quad f : x \mapsto \sqrt{x + 1} - \sqrt{x}$ .

Question 2 :
L’équation $\sqrt{x + 1} - \sqrt{x} = y$ admet une et une seule solution ssi $y \in \; ]0 , 1]$ .

Question 3 :
Déterminer la solution de l’équation $f(x) = y$ .

Correction de l’exercice sur la résolution d’équations en continuité en Terminale

Question 1 :
La fonction $f : x \mapsto \sqrt{x + 1} - \sqrt{x}$ est continue sur $[0 ,\, +\infty[$ .

En utilisant la quantité conjuguée, on l’écrit $f(x) = \displaystyle \frac {(x + 1) - x} {\sqrt{x + 1} + \sqrt{x}}$
$f(x) = \displaystyle \frac {1} {\sqrt{x + 1} + \sqrt{x}}$ .

$\bullet$ Comme $\displaystyle \lim_{x \to + \infty}{\sqrt{x + 1} + \sqrt{x}} = + \infty$
$\displaystyle \lim_{x \to + \infty}f(x) = 0$ .

$\bullet$ $x \mapsto \sqrt{x + 1} + \sqrt{x}$ est strictement croissante, comme somme de fonctions strictement croissantes, et à valeurs strictement positives, la fonction inverse $f$ est strictement décroissante sur $[0 , + \infty[$ .

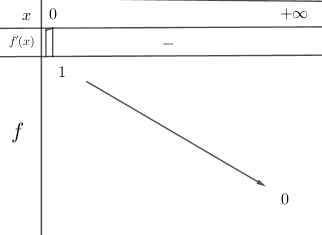
Question 2 :
On en déduit que si $y \notin [0 , 1[$ , l’équation $f(x) = y$ n’admet pas de solution.
et $f(x) = 0$ ssi $x = 0$ .
Dans la suite, on suppose que $y \in \; ]0 , 1[$ .

On traduit $\displaystyle \lim_{x \to + \infty} f(x) = 0$ , en prenant l’intervalle ouvert $]- y , y[$ contenant $0$ , il existe $A > 0$ tel que si $x \geqslant A, \, f(x) < y$
alors $y \in\; ]f(0) ,\, f(A)[$ . Donc par le théorème des valeurs intermédiaires, il existe $a \in \;]0 , A[$ tel que $f(a) = y$ .

Par la stricte croissance de $f$ , la solution de $f(x) = y$ est unique.

Question 3 :
Si $y = \sqrt{x+ 1} - \sqrt{x}$ , on en déduit en élevant au carré que
$y ^2 = (x + 1) + x - 2\,\sqrt{x(x + 1)}$
donc $2 \,x + 1 - y^2 = 2\,\sqrt{x(x + 1)}$
en élevant au carré, on obtient la condition nécessaire :
$(2 \,x + 1 - y^2 ) ^2 = 4\,x(x + 1)$
ssi $(2\, x + 1)^2 - 2 \, y^2 \, (2\, x + 1) + y^4$ $\qquad \qquad \qquad = 4\, x^2 + 4 \, x$
ssi $4 \, x^2 + 4\, x + 1 - 4 \, x \, y^2 - 2\, y^2 + y ^4$ $\qquad \qquad \qquad = 4\, x^2 + 4 \, x$
ssi $4 \, x\, y^2 = y ^4 - 2\, y^2 + 1$
ssi $x = \displaystyle \frac {(y ^2 - 1)^2} {4 \, y ^2}$ .

On n’a pas raisonné par équivalence mais obtenu une seule valeur possible comme solution de l’équation.
Comme on sait que cette équation admet une seule solution, on a bien obtenu la solution de l’équation cherchée.
Elle est donc égale à 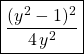$\boxed{ \displaystyle \frac {(y ^2 - 1)^2} {4 \, y ^2}}$ .

4. Les équations polynomiales

Exercice sur les équations polynomiales en Terminale

Question 1 :
Soit $f : x \mapsto x ^3 - 2\, x^2 - 1$ .
Montrer que l’équation $f(x) = 0$ admet une unique racine $a$ et l’encadrer entre deux entiers consécutifs $p$ et $p + 1$ .
$p =$ ?

Question 2 :
On définit $g : \;]0 , + \infty[ \to \mathbb{R}, \, x \mapsto \displaystyle 2 + \frac 1 {x^2}$ .
$g(a) =$ ?

Question 3 :
On définit la suite $g : \;]0 , + \infty[ \to \mathbb{R}, \, x \mapsto (u_n)_n$ par $u_ 0 = 2$ et si $n \in \mathbb{N}$ , $u_{n + 1} = g(u_n)$ .
Pour tout $n \in \mathbb{N} , \, 2 \leqslant u_{2 n}\leqslant a \leqslant u_{2 n + 1} \displaystyle 2 + \frac 1 {x^2}$ .
Vrai ou Faux ?

Correction de l’exercice sur les équations polynomiales en Terminale

Question 1 :
$p =$ 2

$f$ est dérivable sur $\mathbb{R}$
et si $x \in \mathbb{R}, f'(x) = x( 3\, x - 4)$ .

$\ast$ $f$ est croissante sur $]- \infty , 0]$ et décroissante sur $[0 , 4/3]$
elle admet un maximum local en $0$ , donc si $x \leqslant 4/3, \, f(x) \leqslant f(0)$ soit $f(x) \leqslant - 1$ .

$\ast$ $f$ est strictement croissante et continue sur $[4/3 , + \infty[$
$f(2) = - 1$ et $f(3) = 27 - 19 = 8$

donc $f$ s’annule une et une seule fois sur $[4/3 , \infty[$ et en particulier $a \in \; ] 2 , 3[$ .

Question 2 :
$g(a) =$ a

$g(a) = \displaystyle \frac {2 \, a^2 + 1} {a ^2} = \frac {a ^3} {a ^2} = a$ .

Question 3 :
Vrai ou Faux ? Vrai

Si $n \in \mathbb{N}$ on note $\mathcal{P}(n) : 2 \leqslant u_{2 n}\leqslant a \leqslant u_{2 n + 1}\,$ .

Initialisation : $u_0 = 2$ et $u_ 1 = 2, 25$
$f(2,25) \approx 0.2626$ , donc $a < 2,25$ .
On a donc prouvé que $\mathcal{P}(0)$ est vraie.

Hérédité : On suppose que $\mathcal{P}(n)$ est vraie. Par stricte décroissance de
la fonction $g$ :
$g(u_{n + 1}) \leqslant g(a) \leqslant g(u_n))$
et en utilisant $g(x) \geqslant 2$ ,
soit $2 \leqslant u_{2 n + 2} \leqslant a \leqslant u_{n + 1}$

puis comme $2 \leqslant u_{2 n + 2} \leqslant a$
par stricte décroissance de $g$
$g(a) \leqslant g(u_{2n + 2})$ soit $a \leqslant u_{2 \, n + 3}$

On a prouvé $\mathcal{P}(n + 1)$ .

Conclusion : la propriété est vraie par récurrence sur $n$ .

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

5. Continuité des suites récurrentes

Exercice sur la continuité des suites récurrentes en Terminale

On considère $f : x \mapsto 2 - (x + 1) \, \textrm{e} ^{- x}$

Question 1 :
Étudier la fonction $f$ sur $\mathbb{R }$ .

Question 2 :
Si $x \leqslant 0, f(x) - x > 0$ .
Vrai ou Faux ?

Question 3 :
Étudier les variations de $\qquad g : x \mapsto f(x) - x$ sur $\mathbb{R}^+$ .
$g$ y est strictement décroissante, Vrai ou Faux ?

Correction de l’exercice sur la continuité des suites récurrentes en Terminale

Question 1 :
$f$ est définie et dérivable sur $\mathbb{R}$ .

$\bullet$ Limite en $+ \infty$
Comme $\displaystyle \lim_{x \to + \infty} \textrm{e} ^{-x} = 0$ et $\displaystyle \lim_{x \to + \infty} x \, \textrm{e} ^{-x} = 0$ (croissance comparée), alors $\displaystyle \lim_{x \to + \infty} f(x)= 2$
La droite d’équation $y= 2$ est asymptote à la courbe en $+\infty$ .

$\bullet$ Limite en $- \infty$
Comme $\displaystyle \lim_{x \to + \infty} -(x + 1) \,\textrm{e} ^{-x} = - \infty$
comme produit de deux fonctions qui tendent vers $+\infty$ si $x \to + \infty$ , alors $\displaystyle \lim_{x \to + \infty} f(x)= +\infty$ .

$\bullet$ Dérivée
Si $x$ est réel, $f'(x) = - \textrm{e} ^{- x} + (x + 1) \, \textrm{e}^{-x} = x\, \textrm{e} ^{- x}$
$f$ est strictement croissante sur $\mathbb{R}^{+}$ et décroissante sur $\mathbb{R}^{-}$ .

Question 2 :
Vrai ou Faux ? Vrai

On note $g(x) = f(x) - x$ .
Si $x \in \mathbb{R} ^{- }$ , $g'(x) = f'(x) - 1 < 0$
$g$ est strictement décroissante sur $]- \infty, 0]$ et $g(0) = 2 - 1 > 0$
donc si $x \in \mathbb{R}^{ - }, \, g(x) > 0$ soit $f(x) > 0$ .

Question 3 :
$g$ y est strictement décroissante, Vrai ou Faux ? Vrai

$g$ est dérivable sur $\mathbb{R}^+$ .

$g'(x) = f'(x) - 1 = x \, \textrm{e} ^{ - x} - 1$
$g''(x) = -x \, \textrm{e} ^{-x} +\textrm{e} ^{ - x}$
$g''(x) = (1 - x) \, \textrm{e}^{ - x}$ est du signe de $1 - x$
$g'$ est croissante sur $[0 , 1]$ et décroissante sur $[1 , + \infty[$ .
Elle admet un maximum en $1$ et $g'(1) = \textrm{e} ^{- 1} - 1 < 0$
donc pour tout $x \geqslant 0$ , $g'(x) \leqslant g'(1) < 0$ .

$g$ est strictement décroissante sur $\mathbb{R}^+$ .

5. Généralisation du théorème des valeurs intermédiaires

Exercice sur la généralisation du théorème des valeurs intermédiaires en Terminale

Question 1 :
$\varphi :\; ]0 , \, 1] \to \mathbb{R}, \, \displaystyle x \mapsto \frac 1 x - 1$ est une fonction continue à valeurs positives ou nulles.
Vrai ou Faux ?

Question 2 :
On suppose que $f$ est continue sur $[0 , + \infty[$ et admet une limite finie $L$ en $+\infty$ .
On note pour $x \in\; ]0 , 1] , \,g(x) = f(\varphi(x))$ et $g(0) = L$ .
$g$ est continue sur $[0 , 1]$ .
Vrai ou Faux ?

Question 3 :
On suppose $L \neq f(0)$
Si $k$ est strictement compris entre $f(0)$ et $L$ , il existe $a \in \mathbb{R}^{+*}$ tel que $k = f(a)$ .
Vrai ou Faux ?

Correction d’exercice sur la généralisation du théorème des valeurs intermédiaires en Terminale

Question 1 :
Vrai ou Faux ? Vrai

$\bullet$ $x \mapsto \displaystyle \frac 1 x$ est continue sur $]0 , \, 1]$ donc $\varphi$ est continue sur $]0 , \, 1]$ .

$\bullet$ Si $x \in \;]0 , 1]$ , $\varphi(x) = \displaystyle \frac {1 - x} x \geqslant 0$ .

Question 2 :
Vrai ou Faux ? Vrai

$\bullet$ Continuité sur $]0 , 1]$ .
$\ast$ $\varphi$ est continue sur $]0 , 1]$ à valeurs dans $[0 , + \infty[$
$\ast$ $f$ est continue sur $[0 , + \infty[$
La composée $g = f \circ \varphi$ est continue sur $]0 , 1]$ .

$\bullet$ $\displaystyle \lim_{x \to 0^{+}} \varphi(x) = + \infty$ et $\displaystyle \lim_{x \to + \infty} f(x) = L$
par composition des limites,
$\qquad \quad \displaystyle \lim_{x \to 0} f(\varphi(x)) = L$ ,
ce qui s’écrit $\displaystyle \lim_{x \to 0} g(x) = g(0)$ ,
ce qui prouve la continuité de $g$ en $0$ .

$g$ est continue sur $[0 , 1]$ .

Question 3 :
Vrai ou Faux ? Vrai

$\bullet$ On applique le théorème des valeurs intermédiaires à la fonction continue $g$ ,
$k$ est strictement compris entre $g(0)$ et $g(1)$ , il existe $c \in \; ]0 , 1[$ tel que $g(c) = k$ .

$\bullet$ On note $a = \varphi(c) > 0$ .
$k = g(c) = f(\varphi(c)) = f(a)$ avec $a > 0$ .

Alors $f$ prend sur $[0 , + \infty[$ toute valeur entre $f(0)$ et $L$ ( $L$ exclu).

6. Déterminer des fonctions, chapitre de la continuité en Terminale

Exercice pour déterminer des fonctions

Soit $f$ une fonction définie sur $\mathbb{R}$ et continue en $0$ telle qu’il existe $a \neq \pm 1$ tel que pour tout réel $x$ , $f(a \, x) = f(x)$

Question 1 :
Si $n \in \mathbb{N}$ , on peut exprimer $f(x)$ en fonction de $f(a^n \, x)$
Vrai ou Faux ?

Question 2 :
Si $\vert a \vert < 1$ , $f$ est constante.
Vrai ou Faux ?

Question 3 :
Si $\vert a \vert > 1$ , $f$ est constante.
Vrai ou Faux ?

Correction de l’exercice pour déterminer des fonctions

Question 1 :
Vrai ou Faux ? Vrai

On établit la formule à démontrer par récurrence en calculant $f(a \, x)$ , $f(a ^2 \, x)$ etc …

Soit $x \in \mathbb{R}$ . On note pour $n \in \mathbb {N}^*$
$\qquad \qquad \mathcal{P}(n) : f(x) = f(a ^n \, x)$ .

Initialisation :
$\mathcal{P}(1)$ est vraie par hypothèse sur $f$ .

Hérédité : On suppose que $\mathcal{P}(n)$ est vraie, en appliquant l’hypothèse sur $f$ au point $a^n \, x$ ,
$f (a \, a^n \, x) = f(a^n \, x) = f(x)$ par $\mathcal{P}(n)$ , ce qui prouve $\mathcal{P}(n + 1)$ .

Conclusion : La propriété est démontrée par récurrence.

Question 2 :
Vrai ou Faux ? Vrai

On suppose que $\vert a \vert < 1$
Comme $\displaystyle \lim_{n \to + \infty} a^n \, x= 0$ , par continuité de $f$ en $0$ , $\displaystyle \lim_{n \to + \infty} f(a^n \, x)= f(0)$ .
Mais comme c’est une suite constante égale à $f(x)$ , on a prouvé que $f(x) = f(0)$ donc $f$ est constante.

Question 3 :
Vrai ou Faux ? Vrai

Si $\vert a \vert > 1$ , en appliquant l’hypothèse sur $f$ à $x/a$ , on obtient pour tout réel $x$ , $f(a \, x / a) = f(x/a)$
soit en notant $b = 1/a$ , pour tout $x$ , $f(x) = f(b \, x)$ avec $f$ continue en $0$ et $\vert b \vert < 1$ .
La question précédente donne $f$ est une application constante.

Pour renforcer vos connaissances, nous vous recommandons de réaliser également les exercices des annales du bac en maths. Si certains chapitres ou certaines notions vous sont difficiles, n’hésitez pas à prendre connaissances des autres cours en ligne de maths au programme de Terminale dont les chapitres suivants :

Exercices et corrigés de maths sur la continuité en Terminale

1. Étude de continuité en Terminale

Exercice 1 sur la continuité en Terminale

Correction de l’exercice 1 sur la continuité en Terminale

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

2. Sur la partie entière, chapitre de continuité en Terminale

Exercice sur la partie entière en continuité

Correction de l’exercice sur la partie entière en continuité

3. Résolution d’équations

Exercice sur la résolution d’équations en continuité en Terminale

Correction de l’exercice sur la résolution d’équations en continuité en Terminale

4. Les équations polynomiales

Exercice sur les équations polynomiales en Terminale

Correction de l’exercice sur les équations polynomiales en Terminale

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

5. Continuité des suites récurrentes

Exercice sur la continuité des suites récurrentes en Terminale

Correction de l’exercice sur la continuité des suites récurrentes en Terminale

5. Généralisation du théorème des valeurs intermédiaires

Exercice sur la généralisation du théorème des valeurs intermédiaires en Terminale

Correction d’exercice sur la généralisation du théorème des valeurs intermédiaires en Terminale

6. Déterminer des fonctions, chapitre de la continuité en Terminale

Exercice pour déterminer des fonctions

Correction de l’exercice pour déterminer des fonctions

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales