Chapitres Maths en Terminale Générale
Exercices et corrigés : Dérivées et convexité en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Préparez-vous au bac en vous exerçant avec nos exercices sur les dérivées et la convexité au programme de Terminale. Prenez le temps de faire chaque exercice à votre rythme et vérifier vos connaissances en comparant vos résultats avec les corrigés d’exercices. Le nouveau programme de maths en Terminale est très lourd et demande beaucoup de travail aux élèves de Terminale. Prendre des cours particuliers en maths en Terminale permet de ne pas se laisser submerger par la charge de travail, et vous assure de bons résultats au bac.
1. Calcul de dérivées en terminale générale
Exercice sur les calcul de dérivée :
On précisera s’il y a lieu l’ensemble des réels où ![]() est dérivable. Puis on donnera une expression simplifiée de la dérivée.
est dérivable. Puis on donnera une expression simplifiée de la dérivée.
Question 1 :
![]()
Question 2 :
![]()
Question 3 :
![]()
Correction de l’exercice sur les calculs de dérivées
Question 1 :
On écrit ![]()
avec ![]() et
et ![]()
Puis on note ![]()
![]() Dérivabilité
Dérivabilité
![]()
![]() est dérivable sur
est dérivable sur ![]() , la fonction exponentielle est dérivable sur
, la fonction exponentielle est dérivable sur ![]() , donc
, donc ![]() est dérivable sur
est dérivable sur ![]() comme composée de fonctions dérivables.
comme composée de fonctions dérivables.
![]()
![]() est une fonction polynôme, donc est dérivable sur
est une fonction polynôme, donc est dérivable sur ![]() ,
,
par produit de fonctions dérivables, ![]() est dérivable sur
est dérivable sur ![]()
![]() Calcul de la dérivée
Calcul de la dérivée
Pour tout réel ![]() ,
,
![]()
![]()
![]()
![]() .
.
Question 2 :
On note ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() , donc
, donc ![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
On écrit ![]() avec
avec ![]() et
et ![]()
![]()
![]() .
.
Donc si ![]()
![]()
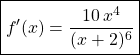 .
.
Question 3 :
![]() Domaine de dérivabilité
Domaine de dérivabilité
![]()
![]() est dérivable sur
est dérivable sur ![]() .
.
La fonction exponentielle est dérivable sur ![]() , donc par composition,
, donc par composition, ![]() est dérivable sur
est dérivable sur ![]() .
.
![]() Calcul de la dérivée
Calcul de la dérivée
Si ![]() ,
, ![]()
 .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Exercices avec des dérivées en Terminale
Exercice sur les dérivées en terminale générale :
Déterminer les fonctions polynômes ![]() non nulles telles qu’il existe un réel
non nulles telles qu’il existe un réel ![]() tel que
tel que ![]() .
.
Correction de l’exercice sur les dérivées :
![]() On cherche le degré d’une solution
On cherche le degré d’une solution ![]() .
.
On suppose que ![]() est une fonction polynôme de degré
est une fonction polynôme de degré ![]() que l’on écrit sous la forme
que l’on écrit sous la forme ![]() où
où ![]() est une fonction polynôme de degré inférieur ou égal à
est une fonction polynôme de degré inférieur ou égal à ![]() .
.
Pour tout réel ![]() ,
, ![]()
alors ![]() avec
avec ![]() fonction polynôme de degré au plus égal à
fonction polynôme de degré au plus égal à ![]() .
.
Si ![]() , on doit avoir
, on doit avoir ![]() ssi
ssi ![]() .
.
![]() On détermine
On détermine ![]() .
.
Dans la suite on cherche donc ![]() avec
avec ![]()
![]()
Pour tout ![]() ,
, ![]()
ssi pour tout réel ![]() ,
, ![]()
On obtient les conditions nécessaires et suffisantes par égalité de deux fonctions polynômes
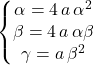
Comme ![]()

ssi 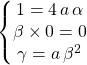 ssi
ssi ![]()
Les solutions non nulles sont les fonctions polynômes ![]()
avec ![]() et dans ce cas
et dans ce cas ![]() .
.
3. La convexité en Terminale Générale
Exercice 1 sur la convexité en terminale :
On note ![]()
et si ![]() ,
, ![]() .
.
Question 1 :
![]()
![]() ?
?
Question 2 :
La fonction ![]()
a. est convexe
b. est concave
c. change de concavité.
Question 3 :
En écrivant l’équation réduite de la tangente en ![]() , trouver une inégalité faisant intervenir
, trouver une inégalité faisant intervenir ![]() valable sur
valable sur ![]() .
.
Exercice 2 sur la convexité en terminale :
![]()
Question 1 :
Pour tout réel ![]() ,
, ![]() avec
avec ![]() .
.
![]() ?
?
Question 2 :
On peut écrire ![]()
avec ![]() ?
?
Question 3 :
Quel est le nombre de points d’inflexion du graphe de ![]() ?
?
On précisera leur(s) abscisse(s).
Nombre ?
Question 4 :
Préciser l’équation réduite de la tangente au point d’abscisse ![]()
Correction de l’exercice 1 sur la convexité en terminale :
Question 1 :
![]() 4;5
4;5
![]() est deux fois dérivable sur
est deux fois dérivable sur ![]()
![]() Dérivée première
Dérivée première
En écrivant ![]()
![]()
![]()
![]() .
.
![]() Dérivée seconde
Dérivée seconde
On écrit ![]()
donc
![]()
![]()
![]()
![]()
Par réduction au même dénominateur
![]()
avec ![]()
![]()
![]()
![]() .
.
 .
.
Question 2 :
![]()
Le discriminant de ![]() est
est ![]() , donc
, donc ![]() pour tout réel.
pour tout réel.
![]() est du signe de
est du signe de ![]() .
.
![]() si
si ![]() et
et ![]() si
si ![]() .
.
![]() change de concavité sur
change de concavité sur ![]() .
.
Mais le graphe n’admet pas de point d’inflexion, puisque ![]() n’est pas définie en
n’est pas définie en ![]() .
.
Question 3 :
![]() et
et ![]() .
.
La tangente a pour équation réduite ![]() soit
soit ![]() .
.
La fonction ![]() est convexe sur
est convexe sur ![]() . La courbe est au dessus de la tangente en
. La courbe est au dessus de la tangente en ![]() :
:
pour tout ![]()
![]() .
.
On peut aussi écrire puisque ![]() ,
,
si ![]() ,
, ![]()
cette inégalité reste vraie en ![]() .
.
Si ![]() ,
, ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice 2 sur la convexité en terminale :
Question 1 :
![]() 2
2
![]() est deux fois dérivable sur
est deux fois dérivable sur ![]()
![]() Dérivée première
Dérivée première
![]()
![]()
![]()
![]()
![]() .
.
![]() Dérivée seconde
Dérivée seconde
comme ci-dessus,
![]()
avec ![]()
![]()
![]()
![]()
![]() .
.
Question 2 :
avec ![]() 4;1
4;1
![]() , on peut factoriser
, on peut factoriser ![]() et écrire
et écrire
![]()
en comparant les termes en ![]() , on obtient
, on obtient ![]() .
.
On développe
![]()
![]()
par unicité de l’écriture d’une fonction polynôme
 ssi
ssi ![]()
donc ![]() .
.
Question 3 :
Nombre = 3
Les racines de ![]() sont
sont ![]() et
et ![]() .
.
![]() et donc
et donc ![]() s’annule en changeant de signe en
s’annule en changeant de signe en
![]() ,
, ![]() et
et ![]()
On a trois points d’inflexion.
Question 4 :
L’équation réduite de la tangente au point d’abscisse 1 est
![]()
![]() ,
, ![]()
![]() .
.
Pour réussir en terminale et plus particulièrement en maths, il est impératif de s’entraîner régulièrement sur des exercices ou sur des annales de maths du bac. Les mathématiques demandent un travail rigoureux et régulier pour obtenir de bonnes notes. Ce travail est d’autant plus important pour les élèves qui souhaitent intégrer les meilleures prepa MP ou les meilleures écoles d’ingénieurs en post-bac. Pour ce faire, les cours en ligne de maths permettent aux élèves de terminale de pouvoir réviser divers chapitres au programme, comme :

