Chapitres Maths en Terminale Générale

Exercices et corrigés : les fonctions logarithmes en Terminale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Revoyez et vérifiez votre niveau de en cours de maths en Terminale en vous testant sur nos cours en ligne gratuits et leurs corrigés d’exercices. Maîtriser le programme de maths en terminale est indispensable pour les élèves qui souhaitent poursuivre leurs études dans les meilleures prepa MPSI ou intégrer les meilleures écoles d’ingénieurs post-bac.

1. Équations de fonction logarithme en Terminale

Exercice sur les équations de fonction logarithme en Terminale Générale

Résoudre les équations d’inconnue $x \in \mathbb{R}$ .

Question 1 :

$6 \, \textrm{e} ^{2 \, x} - 5 \, \textrm{e} ^x + 1 = 0$ .

Question 2 :

$\ln(x - 3) + \ln(x + 1) = \ln(x ^2 + 5)$

Question 3 :

$\ln(3 - x) + \ln(3 + x) = \ln (11 - 3 \,x)$

Question 4 :

$\ln(6\, x -2)+\ln(2\,x -1) = \ln(x)$ .

Question 5 :

$\ln(3 \, x + 1) + \ln(3 \, x - 2)$ $\qquad \qquad \qquad = \ln(x ^2 - x + 1)$ .

Correction de l’exercice sur les équations de fonction logarithme en Terminale Générale

Question 1 :

Solution : -ln(3);-ln(2)

En notant $t = \textrm{e} ^x$ , on résout l’équation : $\qquad \qquad 6 \, t ^2 - 5 \, t + 1 = 0$ dont le discriminant est $\Delta = 25 - 24 = 1$ et les racines sont

$\quad \displaystyle \frac {5 - 1} {12} = \frac 1 3$ et $\displaystyle \frac {5 + 1} {12} = \frac 1 2$ .

Il reste à résoudre

$\displaystyle \textrm{e} ^x = \frac 1 3$ ssi $\displaystyle x = \ln\left (\frac 1 3 \right ) = - \ln (3)$

et $\displaystyle \textrm{e} ^x = \frac 1 2$ ssi $x =\displaystyle \ln \left (\frac 1 2 \right ) = - \ln (2)$ .

L’ensemble des solutions est $\qquad \boxed{\mathcal{S} = \{ -\ln(3) ,-\ln( 2)\}}$ .

Question 2 :

Solution : pas de solution

On suppose que $x > 3$ , $x > - 1$ ssi $x > 3$

Sous la condition $x > 3$ , l’équation est équivalente à

$\ln\left ( (x - 3) \,(x + 1)\right ) = \ln(x ^2 + 5)$

ssi $(x - 3) \,(x + 1) = x ^2 + 5$

ssi $x ^2 - 3\, x + x - 3 = x^2 + 5$

ssi $2\, x = - 8$ ssi $x = - 4$ .

Comme $-4$ n’est pas dans l’ensemble de définition, l’équation n’a pas de solution.

Question 3 :

Solution : 1;2

On suppose que

$3 - x > 0$ , $3 + x > 0$ et $11 - 3 \, x > 0$

ssi $x < 3$ , $x > - 3$ et $x < 11/3$

ssi $- 3 < x < 3$ .

Sous ces conditions, l’équation est équivalente à

$\ln ((3 - x)(3 + x)) = \ln (11 - 3 \,x)$

ssi $9 - x^2 = 11 - 3 \, x$

ssi $x ^2 - 3 \, x + 2 = 0$ .

$1$ est racine évidente de cette équation, l’autre est donc égale au produit $2$ des racines.

Les valeurs $1$ et $2$ vérifient les conditions imposées à $x$ , donc l’ensemble des solutions est $\boxed{\mathcal{S} = \{ 1 , 2\}}$ .

Question 4 :

Solution : 2/3

On suppose que $6\, x -2 > 0$ , $2 \, x - 1 > 0$ et $x > 0$ ssi $x > 1/2$ .

Sous cette condition, l’équation est équivalente à

$\quad \ln((6\, x -2)(2\,x -1)) = \ln(x)$

soit à $(6\, x -2)(2\,x -1) = x$

par stricte croissance de la fonction $\ln$ .

On obtient la condition nécessaire et suffisante :

$12 \, x ^2 - 4 \, x - 6 \, x + 2 = x$

ssi $12\, x ^2 - 11 \, x + 2 = 0$

dont le discriminant est égal à $\Delta = 121 - 8 \times 12 =25$ et les racines sont $\displaystyle \frac {11 + 5} {24} = \frac 2 3$ et

$\displaystyle \frac {11 - 5} {24 } = \frac 1 4$ .

Seule $\displaystyle \frac {2} 3$ vérifie $\displaystyle \frac {2} 3 > \frac 1 2$ .

L’équation admet une unique solution $\boxed{\displaystyle \frac {2} 3}$ .

Question 5 :

Solution : 3/4

Pour tout réel $x$ , $x ^2 - x + 1 > 0$ car le discriminant est égal à $\Delta = - 3$ .

On suppose que

$3 \, x + 1 > 0$ et $3 \, x - 2 > 0$ ssi $x > 2 /3$ .

Sous cette condition, l’équation est équivalente à

$\ln((3\, x + 1) (3 \, x - 2) ) = \ln(x ^2 - x + 1)$

soit à $(3\, x + 1) (3 \, x - 2 ) = x ^2 - x + 1$

ssi $9\, x ^2 + 3 \, x - 6 \, x - 2 = x ^2 - x + 1$

ssi $8\, x ^2 - 2 \, x - 3 = 0$

dont le discriminant vaut $\qquad \qquad \Delta = 4 + 96 = 100$ .

Les deux racines sont $\displaystyle \frac {2 + 10} {16} = \frac 3 4$ et $\displaystyle \frac {2 - 10} {16} = \frac {-1} 2$ .

$\displaystyle \frac 3 4 - \frac 2 3 = \frac {9 - 8} {12} > 0$

Seule $3 /4$ est supérieure à $2/3$ , c’est la seule solution de l’équation.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

2. Inéquations de fonction logarithme en Terminale Générale

Exercice sur les inéquations de fonction logarithme en Terminale

Question 1 :

L’ensemble des solutions de $\qquad \quad 4 \, \textrm{e} ^x + 2 \, \textrm{e} ^{ - x} > 9$ est

$] - \infty\, , \, a \, \ln(b)[\, \cup \, ] \ln(c)\, , \, + \infty[$

avec $a,b,c$ = ?

Question 2 :

L’ensemble des solutions de

$\qquad \quad 7 \, \textrm{e} ^x < \textrm{e} ^{2 \, x} + 1 2 < 8 \, \textrm{e} ^{ x}$ est $\mathcal{S} = ]\ln(a) ,\, \ln(b)[\, \cup \, ] c \, \ln(c) , \, \ln(d) [$ .

avec $a,b,c,d =$ ?

Correction de l’exercice sur les inééquations de fonction logarithme en Terminale

Question 1 :

avec $a,b,c$ = -2,2,2

En notant $t = \textrm{e} ^x$ , on résout l’équation : $\qquad \qquad \displaystyle 4 \, t + \frac {2} t > 9$ .

Comme $t > 0$ elle est équivalente à $\qquad \qquad 4 \ t ^2 - 9 \, t + 2 > 0$ .

Le discriminant de l’équation $4 \ t ^2 - 9 \, t + 2 = 0$ est $\Delta = 81 - 32 = 49$

Cette équation admet deux racines distinctes $\displaystyle \frac{ 9 - 7} 8 = \frac 1 4$ et $\displaystyle \frac{ 9 + 7} 8 = 2$ .

On écrit donc $\displaystyle 4 \, t + \frac {2} t > 9$

ssi $(4 \, t - 1) (t - 2) > 0$

ssi $t > 2$ ou $t < 1/4$ .

Donc l’inéquation proposée est équivalente à $\textrm{e} ^x > 2$ ou $\textrm{e} ^x < 1 / 4$

ssi $x > \ln(2)$ ou $x < - 2 \; \ln(2)$ .

$\mathcal{S} =\; ] - \infty, - 2 \, \ln(2)[\; \cup \; ] \ln(2) , + \infty[\;$ .

Question 2 :

avec $a,b,c,d =$ 2,3,2,6

$7 \, \textrm{e} ^x < \textrm{e} ^{2 \, x} + 1 2 < 8 \, \textrm{e} ^{ x}$

ssi $\left \{ \begin{matrix} \textrm{e} ^{2 \, x} + 1 2 - 7 \, \textrm{e} ^x > 0 \\ \textrm{e} ^{2 \, x} + 1 2 - 8 \, \textrm{e} ^{ x} < 0 \end{matrix} \right.$

soit en posant $t = \textrm{e} ^{ x}$

ssi $\left \{ \begin{matrix} t ^2 - 7 \, t + 12 > 0\\ t ^2 - 8 \, t + 12 < 0 \end{matrix} \right.$

$\ast$ Le discriminant $\Delta$ de $t ^2 - 7\, t + 12 = 0$ est $\Delta = 49 - 48 = 1$ , les racines sont $3$ et $4$ , ce qui donne la factorisation

$\quad t ^2 - 7 \,t + 12 = (t - 3)(t - 4)$ .

$\ast$ Le discriminant $\Delta$ de $t ^2 - 8\, t + 12 = 0$ est $\Delta = 64 - 48 = 16$ , les racines sont $2$ et $6$ , ce qui donne la factorisation

$\quad t ^2 - 8 \, t + 12 = (t - 2)(t - 6)$ .

On résout en premier lieu le système d’inéquations

$\left \{ \begin{matrix} (t - 3)(t - 4) > 0\\ (t - 2)(t - 6)< 0 \end{matrix} \right.$

ssi $\left \{ \begin{matrix} t < 3 \textrm { ou } t > 4\\ 2 < t < 6 \end{matrix} \right.$

en s’aidant si nécessaire d’un tableau de signes, on obtient $2 < t < 3$ ou $4 < t < 6$ .

On rappelle que $t = \textrm{e} ^{ x}$ .

On a donc obtenu

$\qquad 2 < \textrm{e} ^{ x} < 3$ ou $4 < \textrm{e} ^{ x} < 6$

ce qui donne par stricte croissance de la fonction $\ln$

$\ln(2) < x < \ln (3)$ ou $\ln(4) < x < \ln(6)$ .

L’ensemble des solutions est $\; \; \; \boxed{\mathcal{S} = ]\ln(2)\, ,\, \ln(3)[\, \cup \, ] 2 \, \ln(2)\, , \, \ln(6) [\;}$ .

3. Systèmes d’équations en Terminale

Exercice sur les systèmes d’équations au programme de terminale

Question 1 :

Résoudre le système $\qquad \left \{ \begin{matrix} \ln(x\, y + y - x - 1) = 1 \\ x \, y + x + y = 2 \end{matrix} \right.$

valeur de $x$ = ?

Question 2 :

Résoudre le système $\qquad \left \{ \begin{matrix} \ln(x) + \ln(y) = 1/2\\ x + y = 4\end{matrix} \right.$

Nombre de solutions ?

Correction de l’exercice sur les systèmes d’équations au programme de terminale

Question 1 :

Valeur de $x$ = (1-e)/2 ou (1-e^1)/2

Le système suppose que $\qquad \quad x \, y + y - x - 1 > 0$

et il s’écrit $\left \{ \begin{matrix} x\, y + y - x - 1 = \textrm{e} ^1 \\ x \, y + x + y = 2 \end{matrix} \right.$

en remplaçant la première équation par la différence de la deuxième et de la première, on obtient un système équivalent :

$\left \{ \begin{matrix} 2\, x = 1 - \textrm{e} \\ x \, y + x + y = 2 \end{matrix} \right.$

ssi $\left \{ \begin{matrix} x = (1 - \textrm{e} )/2 \\ (x + 1) \, y = 2 - x \end{matrix} \right.$

ssi $\left \{ \begin{matrix} x = (1 - \textrm{e} )/2 \\ (3 - \textrm{e}) \, y = 3 + \textrm{e} \end{matrix} \right.$

ssi $\displaystyle x = \frac {1 - \textrm{e}} 2$ et $y = \displaystyle \frac {3 + \textrm{e}}{3 - \textrm{e}}$

Dans ce cas, $x\, y + y - x - 1 = \textrm{e} > 0$ , donc les réels obtenus sont bien solutions

Le système admet une unique solution : $\qquad \quad \displaystyle \boxed{x = \frac {1 - \textrm{e}} 2 }$ et $\boxed{y = \displaystyle \frac {3 + \textrm{e}}{3 - \textrm{e}}}$ .

Question 2 :

Nombre de solutions : 2

On impose donc $x > 0$ et $y > 0$ et le système est équivalent à

$\quad \left \{ \begin{matrix} \ln(x \, y) = 1\\ x + y = 4\end{matrix} \right.$ ssi $\left \{ \begin{matrix} x\, y = \textrm{e} \\ x + y = 4\end{matrix} \right.$

$x$ et $y$ sont les racines de l’équation

$\qquad t ^2 - s \, t + p = t ^2 - 4 \, t + \textrm{e} = 0$

de discriminant $\qquad \Delta = 16 - 4 \,\textrm{e} = 4 \, ( 4 - \textrm{e} ) > 0$ .

On obtient deux racines $t _ 1 = \displaystyle \frac{ 4 - 2 \sqrt{4 - \textrm{e}}} 2 = 2 - \sqrt{4 - \textrm{e}}$ et $t_2 =2 + \sqrt{4 - \textrm{e}}$ .

Il y a deux couples solutions

$\;\; (x , y) = (t_1 \,,\, t_2)$ et $(x , y) = (t_2 \,,\, t_1)$ .

4. Calculs de dérivées de fonctions log en Terminale

Exercice sur les calculs de dérivées en terminale générale

Dans cette partie, préciser le domaine de dérivabilité et calculer la dérivée des fonctions suivantes :

Question 1 :

$x \mapsto \ln(x ^2 + x + 1)$ .

Question 2 :

$x \mapsto \ln(9 - x^2)$ .

Question 3 :

$x \mapsto \ln(6\, x^2 + x - 1)$ .

Question 4 :

$x \mapsto \ln(2\, \textrm{e} ^{x} - \textrm{e} ^{ - x} +1)$ .

Correction de l’exercice sur les calculs de dérivées en terminale générale

Question 1 :

Le discriminant de $x ^2 + x + 1= 0$ est $\Delta = - 3 < 0$ , donc pour tout réel $x$ , $x ^2 + x + 1 > 0$ .

On note $u : x \mapsto x ^2 + x + 1$ .

La fonction $f : x \mapsto \ln(x ^2 + x + 1)$ est dérivable sur $\mathbb{R}$ par composition et

$f'(x) = \displaystyle \frac {u'(x)} {u(x)}$ , $\boxed{f'(x) = \displaystyle \frac {2 \, x + 1} {x ^2 + x + 1} }$ .

Question 2 :

$\bullet$ Dérivabilité

Soit $u : x \mapsto 9 - x^2$

$u(x) = (3 - x)(3 + x)$ ,

$u(x) > 0$ ssi $x \in \; ] - 3 , 3[$ .

La fonction $f : x \mapsto \ln(u(x))$ est dérivable sur $] - 3 , 3[$ par composition de fonctions dérivables.

$\bullet$ Dérivée si $x \in\; ] - 3 , 3[$ ,

$f'(x) = \displaystyle \frac {u'(x)} {u(x)}$ , $\boxed{f'(x) = \displaystyle \frac {- 2 \, x} {9- x^2} }$ .

Question 3 :

$\bullet$ Dérivabilité

Soit $u : x \mapsto 6\, x^2 + x - 1$ .

Le discriminant est égal à $\qquad \quad \Delta = 1 + 24 = 25$ .

Les racines de $u(x) = 0$ sont donc $\displaystyle \frac { - 1 - 5} {12} = \frac {- 1} 2$ et $\displaystyle \frac { - 1 + 5} {12} = \frac {1} 3$

donc $u(x) = (3 \, x - 1) (2 \, x + 1)$

$u(x) > 0$ ssi $x < -1/2$ ou $x > 1/3$ .

$f : x \mapsto \ln(u(x))$ est dérivable sur $\qquad \boxed{\mathcal{D} =\; ] - \infty, - 12[ \, \cup \, ]1/3 , + \infty[\,}$ .

$\bullet$ Dérivée

$f'(x) = \displaystyle \frac {u'(x)} {u(x)}$ , $\boxed{f'(x) = \displaystyle \frac {12 \, x + 1} {6\, x^2 + x - 1} }$ .

Questions 4 :

$\bullet$ Dérivabilité

On note $u(x) = 2\, \textrm{e} ^{x} - \textrm{e} ^{ - x} + 1$ et $t = \textrm{e} ^{x}$

$u(x) =\displaystyle 2 \, t - \frac 1 t + 1 = \frac 1 t \left ( 2 \, t ^2 + t - 1 \right )$

$-1$ est racine évidente de $\qquad \quad 2 \, t ^2 + t - 1= 0$ ,

l’autre racine est égale à l’opposé $-1/2$ du produit des racines donc à $1/2$ .

On peut factoriser $\qquad 2 \, t ^2 + t - 1 = (2 \, t - 1) (t + 1)$

et donc $u(x) = \displaystyle \frac {(2 \, t - 1) (t + 1)} t$

soit $u(x) = \textrm{e} ^{ - x} \left ( \textrm{e} ^x + 1 \right ) \, \left ( 2\, \textrm{e} ^x -1 \right )$ .

$u(x)$ est du signe de $2\, \textrm{e} ^x -1$ .

$u(x) > 0$ ssi $2\, \textrm{e} ^x -1 > 0$ ssi $x > \displaystyle \ln \left( \frac 1 2 \right )$ ssi $x > - \ln(2)$ .

$f$ est dérivable sur $\boxed{\; ] - \ln(2) , \, + \infty[\; }$ par composition.

$\bullet$ Dérivée

$f'(x) = \displaystyle \frac {u'(x)} {u(x)}$ avec $u'(x) = 2\, \textrm{e} ^{x} + \textrm{e} ^{ - x}$
donc $f'(x) = \displaystyle \frac {2\, \textrm{e} ^{x} + \textrm{e} ^{ - x}} {2\, \textrm{e} ^{x} - \textrm{e} ^{ - x} + 1}$
qui est aussi égal à :
$f'(x) = \displaystyle \frac {2\, \textrm{e} ^{2\, x} + 1} {2\, \textrm{e} ^{2\, x} + \textrm{e} ^{ x} - 1}\;$ .

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

5. Calculs de limites de fonction logarithme

Exercice sur le calcul de limites en terminale générale

Question 1 :
$\displaystyle \lim_{x \to 0 ^+ } (x - \ln(x))$ .

Valeur ?

Question 2 :
$\displaystyle \lim_{x \to +\infty} (x - \ln(x))$ .

Valeur ?

Question 3 :
$\displaystyle \lim_{x \to+ \infty } \frac {\ln(x) + 1} {\ln(x)}$ .

Valeur ?

Correction de l’exercice sur le calcul de limites en terminale générale

Question 1 :
Valeur = $+\infty$

$\displaystyle \lim_{x \to 0 ^+ } \ln(x) = - \infty$ et $\displaystyle \lim_{x \to 0 ^+ } x = 0$ donc $\boxed{\displaystyle \lim_{x \to 0 ^+ } (x - \ln(x) ) =+ \infty}$ .

Question 2 :
Valeur = $+\infty$

C’est une forme indéterminée $\infty - \infty$ .

$\displaystyle f(x) = x - \ln(x) = x \, \left (1 - \frac {\ln(x)} x \right )$
avec $\displaystyle \lim_{x \to +\infty} \frac {\ln(x)} x = 0$ donc
$\displaystyle \lim_{x \to +\infty} \left (1 - \frac {\ln(x)} x \right ) = 1$
puis par produit, $\displaystyle \boxed{\lim_{x \to+ \infty}(x - \ln(x)) = + \infty}$ .

Question 3 :
Valeur = 1

C’est une forme indéterminée $\displaystyle \frac {\infty} {\infty}$ .

$f(x) = \displaystyle 1 + \frac { 1} {\ln(x)}$
avec $\displaystyle \lim_{x \to+ \infty } \frac {1} {\ln(x)} = 0$
donc $\displaystyle \boxed{ \lim_{x \to+ \infty } \frac {\ln(x) + 1} {\ln(x)} = 1}$ .

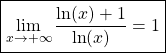Prenez de l’avance sur le programme de terminale avec les annales de maths au bac. Pour réussir le bac, il faut tout au long des années lycées fournir un travail sérieux et régulier. Les révisions sur les cours en ligne de maths en terminale permettent aux élèves de pouvoir se maintenir à niveau tout au long de l’année. Prenez ainsi de l’avance sur le programme avec les chapitres qui suivent :

Les élèves qui rencontrent des difficultés dans n’importe quelle matière, sont invités à prendre des cours particuliers au lycée. Les élèves trouveront de nombreux avantages à cet accompagnement. Les cours particuliers de maths permettront aux élèves d’adopter entre autres les bonnes méthodes de calcul et de raisonnement.

Exercices et corrigés : les fonctions logarithmes en Terminale

1. Équations de fonction logarithme en Terminale

Exercice sur les équations de fonction logarithme en Terminale Générale

Correction de l’exercice sur les équations de fonction logarithme en Terminale Générale

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

2. Inéquations de fonction logarithme en Terminale Générale

Exercice sur les inéquations de fonction logarithme en Terminale

Correction de l’exercice sur les inééquations de fonction logarithme en Terminale

3. Systèmes d’équations en Terminale

Exercice sur les systèmes d’équations au programme de terminale

Correction de l’exercice sur les systèmes d’équations au programme de terminale

4. Calculs de dérivées de fonctions log en Terminale

Exercice sur les calculs de dérivées en terminale générale

Correction de l’exercice sur les calculs de dérivées en terminale générale

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

5. Calculs de limites de fonction logarithme

Exercice sur le calcul de limites en terminale générale

Correction de l’exercice sur le calcul de limites en terminale générale

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales