Chapitres Maths en Terminale Générale

Exercices et corrigés : Les graphes en Terminale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Le niveau attendu au baccalauréat de mathématiques pour l’option maths expert est très élevé. Les élèves doivent donc s’entraîner de manière régulière sur des exercices et les annales. Afin de bien suivre le rythme des cours, les élèves ont la possibilité de prendre des cours particuliers ou d’effectuer des stages intensifs

1. Des exercices sur les Graphes en Terminale, Maths Expertes

Exercices avec les matrices d’adjacence

Question 1 :

Représenter le graphe suivant :
Les sommets sont les points $[\![1 , 6]\!]$ et deux sommets $i$ et $j$ sont liés par un arc lorsque $i \leqslant j$ .
Écrire sa matrice d’adjacence.

Question 2 :

Le nombre d’entiers à 8 chiffres choisis entre $1$ et $6$ formant une suite croissante est égal à $\displaystyle \binom {13} 8$

Question 3 :

Quel est le nombre d’entiers à 10 chiffres formant une suite croissante commençant par $1$ et finissant par $6$ ?

Question 4 :

Le nombre de solutions dans $\mathbb{N}^{6}$ de l’équation $\;\; x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 8$
est égal à ?

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Deuxième partie d’exercices sur les graphes en Maths Expertes

Exercice 1 :

Au cours d’une soirée, les convives se serrent les mains les uns les autres (jamais plusieurs fois avec la même personne). Chacun se souvient du nombre de mains qu’il a serrées.

Question 1 :

Montrer qu’il y a au moins 2 personnes ayant serré le même nombre de mains.

Question 2 :

Le nombre de personnes ayant serré un nombre impair de mains est pair.

2 – Exercices sur les graphes orientés en terminale maths expertes

Encore un exercice pour après la crise sanitaire !
M. et Mme Euler assistent à une réunion. Il y a trois autres couples dans l’assistance et plusieurs poignées de mains sont échangées. Personne ne serre sa propre main et les époux ne se serrent pas la main. Deux personnes quelconques de l’assemblée se serrent la main au plus une fois. M. Euler constate que les 7 autres personnes ont échangé des poignées de mains en nombres tous distincts.

Combien de poignées de mains M. et Mme Euler ont-ils échangé avec les autres membres de la réunion ?
(a pour le nombre de mains de Mr Euler et $b$ pour Mme)

Correction des exercices sur les graphes au programme de terminale

Correction d’exercice sur les matrices d’adjacence en terminale

Question 1 :

C’est un graphe orienté.

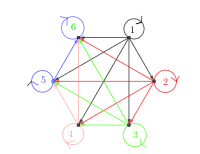
La matrice d’adjacence est la matrice $M = \begin{pmatrix} 1&1&1&1&1&1\\0&1&1&1&1&1\\0&0&1&1&1&1\\0&0&0&1&1&1\\0&0&0&0&1&1\\0&0&0&0&0&1\end{pmatrix}$

Question 2 :

On détermine la matrice $M^7$ , le terme d’indice $i,j$ est le nombre de chemins de $7$ arcs liant le sommet $i$ au sommet $j$ , donc le nombre d’entiers de $8$ chiffres entre $1$ et $6$ (il y a un sommet de plus que d’arcs) est égal à $m_{i,j}^{(7)}.$

En additionnant les éléments de la matrice $M^7$ , on obtient le nombre de d’entiers de $8$ chiffres choisis entre $1$ et $6$ et rangés par ordre croissant.

$M ^7 = \begin{pmatrix} 1&7&28&84&210&462\\0&1&7&28&84&210\\0&0&1&7&28&84\\0&0&0&1&7&28\\0&0&0&0&1&7\\0&0&0&0&0&1\end{pmatrix}$

Le nombre d’entiers répondant à la question commençant par

$1$ est $1+7+28+84+210+462 = 792$
$2$ est $1+7+28+84+210 = 330$
$3$ est $1+7+28+84 = 120$
$4$ est $1+7+28 = 36$
$5$ est 8 et un seul commence par $6$ .

Ce qui donne $N = 792+330+120+36+8+1 = 1287$

et $\displaystyle \binom{13} 8 =1287$ .

Question 3 :

Première solution

C’est le nombre d’entiers de 8 chiffres formant une suite croissante (il suffit de transformer un tel entier $x$ en $1x6$ , et réciproquement on transforme $1x6$ en $x$ , entier de 8 chiffres formant une suite croissante.)

Deuxième solution

on calcule $M ^9$ et l’élément $m_{1,6}^{9}$

$\begin{pmatrix}1&9&45&165&495&1287\\0&1&9&45&165&495\\0&0&1&9&45&165\\0&0&0&1&9&45\\0&0&0&0&1&9\\0&0&0&0&0&1\end{pmatrix}$

Question 4 :

À toute solution de cette équation, on associe un nombre entier de $8$ chiffres formés par $x_1$ fois $1$ , $x_2$ fois 2, $x_3$ fois $3$ , $x_4$ fois 4, $x_5$ fois 5 et $x_6$ fois 6.

Il y a autant de solutions que d’entiers étudiés dans la question 2.

Le nombre de solutions est 1287

Plus généralement si $n, p$ sont des entiers tels que $n \geqslant 2$ et $p \geqslant 2$ , on peut démontrer que

$\bullet$ le nombre d’éléments entiers $(y_1\,,\, \cdots \,,\, y_p)$ tels que $\qquad 1\leqslant y_1 \leqslant\, \cdots \, \leqslant y_p \,\leqslant n$
est égal à $\displaystyle \binom {n + p - 1} p$ .

$\bullet$ le nombre de solutions dans $\mathbb{N}^p$ de l’équation $x_1 + x_2 + \cdots + x_{n - 1 } + x_n = p$ est égal à $\displaystyle \binom {n + p - 1} p$ .

Correction du deuxième exercice sur les matrices d’adjacence

Question 1 :

On construit le graphe non orienté $\Gamma = (\mathcal{S} , \mathcal{A})$ , où $\mathcal{S}$ associe un sommet à chaque convive, et $\mathcal{A}$ associe une arête à chaque couple de convives qui se sont serrés la main. Le nombre de mains serrées par une personne correspond alors au degré du sommet correspondant dans le graphe.

C’est un graphe simple : il n’a pas de boucle et une seule arête au plus entre deux personnes.

Montrer qu’il y a au moins 2 personnes ayant serré le même nombre de mains revient à montrer qu’il y a au moins 2 sommets ayant le même degré.

S’il y a n sommets, le degré d’un sommet est compris entre 0 (cas où le sommet est isolé, c’est à dire que la personne correspondante n’a serré la main à personne) et $n - 1$ (cas où le sommet est relié à tous les autres, c’est à dire que la personne correspondante a serré la main à toutes les autres). <

Pour que tous les sommets aient un degré différent, il faut donc qu’il y ait exactement un sommet de degré 0, un sommet de degré 1, … etc … et un sommet de degré $n - 1$ . Or, s’il y a un sommet de degré $n - 1$ , il ne peut pas y avoir de sommet de degré 0.

De même s’il y a un sommet de degré $0$ , il ne peut y avoir un sommet de degré $n - 1$ .

Il n’y a donc que $n - 1$ valeurs possibles pour les degrés des $n$ sommets, donc il y a au moins $2$ sommets de même degré, donc deux personnes ont serré le même nombre de mains.

Question 2 :

Le nombre de personnes ayant serré un nombre impair de mains est égal au nombre de sommets de degré impairs.

On note $1 , 2 , \cdots , n$ les sommets et $d(i)$ le degré du sommet $i$ .

On note $\mathcal{P} = \{ i \in [[1 , n]] \, :\, d(i) \textrm{ est pair} \}$

et $\mathcal{I} = \{ i \in [[1 , n]] \, :\, d(i) \textrm{ est impair} \}$

$\mathcal{P}$ et $\mathcal{I}$ est une partition de

$\qquad \qquad \{ d(i) \,/\, i \in [[1 , n]] \}$ .

Si $A$ est le nombre de d’arêtes :

$2 \, A = \displaystyle \sum _ {i = 1} ^n d(i)$

$2 \, A = \displaystyle \sum _ {p \in \mathcal{P}} d(p) + \sum _ { i\in \mathcal{I} } d(i)$

il existe $P \in \mathbb{N}$ tel que $\displaystyle \sum _ {p \in \mathcal{P}} d(p) = 2 \, P$ (on additionne des nombres pairs)

donc $\displaystyle \sum _ { i\in \mathcal{I} } d(i)$ est pair, alors $\textrm{Card} \mathcal{I}$ est pair.

Il y a donc un nombre pair de sommets impairs, donc un nombre pair de personnes ayant serré un nombre impair de mains.

De façon plus générale, on retiendra que, pour tout graphe simple non orienté,

$\bullet$ il existe au moins deux sommets du graphe ayant un même degré ;

$\bullet$ la somme des degrés de tous les sommets du graphe est paire et est égale à deux fois le nombre d’arêtes ;

$\bullet$ il y a un nombre pair de sommets qui ont un degré impair.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Correction des exercices sur les graphes orientés en terminale

Question 1 :

On traduit le problème par un graphe, dont les sommets sont les 8 personnes ( $E$ pour Monsieur Euler et $e$ pour Madame Euler) les arêtes représentent une poignée de mains entre les deux sommets correspondants.

Les observations de Monsieur Euler concernent le nombre de poignées de mains serrées par les 7 autres personnes.

Une personne peut serrer la main d’au plus 6 autres personnes.

Si les nombres de poignées de mains échangées sont tous distincts, ce sont nécessairement les nombres 6, 5, 4, 3, 2, 1 et 0.

$\ast$ Une personne que l’on note $S6$ a échangé 6 poignées de mains ; elle a échangé une poignée de mains avec toutes les personnes à qui elle pouvait serrer la main. c’est donc son conjoint $CS6$ qui n’en a échangé aucune.
$S6$ a serré la main de Monsieur Euler et de Madame.

$\ast$ Une personne que l’on note $S5$ échange 5 poignées de mains (avec des personnes qui ne peuvent donc être $CS6$ et son conjoint $CS5$ ), elle en a déjà échangé 1 avec $S6$ , pour les 4 autres poignées, ce sont les deux derniers couples.

Elle serre donc la main de Monsieur Euler et de Madame.

La personne qui échange une seule poignée de mains ne peut être que son conjoint, puisque les membres des couples non encore étudiés ont déjà au moins échangé 2 poignées de mains).

Donc le degré du conjoint de $S5$ noté $CS5$ est égal à 1 (et il a échangé une poignée avec $S6$ ).

$\ast$ Une personne notée $S4$ échange $4$ poignées de mains. Elle a déjà échangé 2 poignées avec $S6$ et $S5$ . Les deux dernières poignées sont échangées avec le dernier couple. Madame Euler a donc échangé au moins 3 poignées de mains.

Donc la personne ayant échangé deux poignées de mains est le conjoint de $CS4$ .

$\ast$ Alors Mme Euler a échangé 3 poignées de mains.

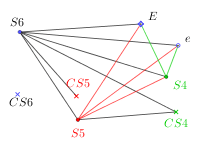
Monsieur Euler a échangé une poignée avec $S6$ , $S5$ , $S4$ , mais pas avec les 3 conjoints correspondants, ni avec Mme Euler, donc Monsieur Euler a échangé 3 poignées.

Pour bien réussir il le bac est essentiel que les élèves maîtrisent les différents chapitres de mathématiques. Le coefficient de l’épreuve de maths est plus élevé pour les élèves ayant choisi l’option maths expertes. Il est essentiel d’améliorer ses acquis, notamment en révisant bien toutes les notions :

Exercices et corrigés : Les graphes en Terminale

1. Des exercices sur les Graphes en Terminale, Maths Expertes

Exercices avec les matrices d’adjacence

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Deuxième partie d’exercices sur les graphes en Maths Expertes

2 – Exercices sur les graphes orientés en terminale maths expertes

Correction des exercices sur les graphes au programme de terminale

Correction d’exercice sur les matrices d’adjacence en terminale

Correction du deuxième exercice sur les matrices d’adjacence

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Correction des exercices sur les graphes orientés en terminale

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales