Chapitres Maths en Terminale Générale

Exercices sur la loi binomiale en Terminale Générale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Exercice du Baccalauréat Liban 2003 sur la Loi Binomiale

Une urne contient quatre boules noires et deux boules blanches. Soit $n$ un entier naturel supérieur ou égal à 2.
On répète $n$ fois l’épreuve qui consiste à tirer une boule puis la remettre dans l’urne ; on suppose que toutes les boules ont la même probabilité d’être tirées et que les tirages sont indépendants.

On note $p_n\,$ la probabilité de tirer exactement une boule blanche lors des $n -1$ premiers tirages et une boule blanche lors du $n$ -ième tirage.

Question 1

Calculer les probabilités $p_2\, , p_3 \,$
(valeurs sous forme de fraction séparées par un point virgule).

Question 2

On considère les évènements suivants

$B_n$ : « On tire une boule blanche lors du $n$ -ième tirage »,
$U_n$ : « On tire une boule blanche et une seule lors des $n -1$ premiers tirages »

a. Calculer la probabilité de l’évène- ment $B_n\,$ .

b. Exprimer la probabilité de l’évène- ment $U_n$ en fonction de $n$ .

c) Pour $n \geqslant 2$ , $p_n = \dfrac {n - 1} 4 \times \dfrac {2 ^{n}} {3 ^n}$

Question 3

On pose : $S_n = p_2 +p_3 + \, \cdots \, +p_n\,$ .
a. Démontrer par récurrence que pour tout entier naturel $n$ supérieur ou égal à 2, on a : $S_n = 1 - \left ( \dfrac n 2 + 1 \right ) \times \dfrac {2 ^{n}} {3 ^n}$

b. Déterminer la limite de la suite $(S_n)_n\,$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Exercice du baccalauréat 2000 sur la Loi Binomiale

Les résultats seront donnés à $10^{-4}$ près.
Une entreprise confie à une société de sondage par téléphone une enquête sur la qualité de ses produits. Chaque enquêteur a une liste de personnes à contacter.

Lors du premier appel téléphonique, la probabilité pour que le correspondant soit absent est $0,4$ .

Si le correspondant est présent, la probabilité pour qu’il accepte de répondre au questionnaire est $0,2$ .

Question 1

On note :
$\ast$ $A_1$ l’évènement « la personne est absente lors du premier appel » ;

$\ast$ $R_1$ l’évènement « la personne accepte de répondre au questionnaire lors du premier appel « .

Quelle est la probabilité de $R_1$ ?

Question 2

Lorsqu’une personne est absente lors du premier appel, on lui téléphone une seconde fois, à une heure différente, et, alors, la probabilité pour qu’elle soit absente est $0,3$ . Et, sachant qu’elle est présente lors du second appel, la probabilité pour qu’elle accepte de répondre au questionnaire est encore $0,2$ .

Si une personne est absente lors du second appel, on ne tente plus de la contacter.

On note :
$A_2$ l’évènement « la personne est absente lors du second appel » ;
$R_2$ l’évènement « la personne accepte de répondre au questionnaire lors du second appel » ;

$R$ l’évènement » la personne accepte de répondre au questionnaire « .

Calculer la probabilité de $R$ .

Question 3

Sachant qu’une personne a accepté de répondre au questionnaire, quelle est la probabilité pour que la réponse ait eu lieu lors du premier appel ?

Question 4

On suppose que les sondages auprès des personnes d’une même liste sont indépendants. Un enquêteur a une liste de 20 personnes à contacter.

Quelle est la probabilité pour qu’au plus 4 des $20$ personnes de la liste acceptent de répondre au questionnaire ? (valeur à $10 ^{-4}$ près)

Exercice sur la loi binomiale : contrôle de production

Une entreprise fabrique chaque jour $10\, 000$ composants électroniques. Chaque composant présente un défaut avec la probabilité $0,002$ .

Si le composant est repéré comme étant défectueux, il est détruit par l’entreprise et chaque composant détruit fait perdre $1$ € à l’entreprise.

Question 1

Les composants sont contrôlés un à un et chaque contrôle coûte $0,1$ €.

Quel est le coût moyen journalier pour l’entreprise (contrôles et destruction des composants défectueux) ?

Question 2

Les composants sont regroupés par lots de $10$ et on effectue un unique contrôle automatique de chaque lot, qui coûte lui aussi $0,1$ euro.

À l’issue de ce contrôle, le lot est accepté si tous les composants sont sains et globalement détruit si l’un au moins des 10 composants présente un défaut.

Quel est le coût moyen journalier pour l’entreprise de ce nouveau dispositif (contrôles et destruction des compo- sants défectueux) ?

Correction de l’exercice baccalauréat Liban sur la loi Binomiale

Question 1

$p_2= \mathbb{P}(B_1\cap B_2) =\dfrac {2}{6} \times \dfrac 2 6 = \dfrac 1 {9}$ .

$p_3 = \mathbb{P}(B_1\cap N_2 \cap B_3 )$ $\qquad \qquad \qquad + \, \mathbb{P}(N_1\cap B_2 \cap B_3 )$

$p_3 = 2 \times \dfrac 1 3 \times \dfrac 2 3\times \dfrac 2 3 = \dfrac {4} {27}$ .

Question 2

a. $\mathbb{P}(B_n) = \dfrac 2 6 = \dfrac 1 3$ .

b. $U_n = (X_{n - 1} = 1)$ où $X_{n - 1}$ est la variable aléatoire égale au nombre de boules blanches obtenues pendant les $n - 1$ premiers tirages.

$X_{n - 1}$ suit une loi binomiale de paramè- tres $n - 1$ et $\dfrac 1 3$ donc

$\mathbb{P}(U_n) = \mathbb{P}(X_{n - 1} = 1)$ $\mathbb{P}(U_n) = \displaystyle \binom {n - 1}\times 1 \dfrac 1 3 \times \left ( \dfrac 2 3 \right ) ^{n - 2}$
$\mathbb{P}(U_n) = \dfrac {(n - 1) \, 2 ^{n - 2} } {3 ^{n - 1} }\;\;$ .

c. $p_n = \mathbb{P}(U_n \cap B_n ) = \mathbb{P}(U_n) \, \mathbb{P}(U_n \, \mid \, B_n)$

$p_n = \dfrac {(n - 1) \, 2 ^{n - 2} } {3 ^{n - 1} }\times \dfrac 1 3 = \dfrac {(n - 1) \, 2 ^{n - 2} } {3 ^{n} }$

On peut donc écrire : $p_n = \dfrac {n - 1} 4 \times \dfrac {2 ^{n}} {3 ^n}$

Question 3

a. On note si $n \in \mathbb{N}$ et $n \geqslant 2$ ,

$\quad \mathcal{P}(n) :$ $S_n = 1 - \left ( \dfrac n 2 + 1 \right ) \times \dfrac {2 ^{n}} {3 ^n}$ .

$\bullet$ Initialisation.

Si $n = 2$ , $S_2 = p _ 2 = \dfrac 1 9$
et $1 - \left ( \dfrac n 2 + 1 \right ) \times \dfrac {2 ^{n}} {3 ^n} = 1 - (1 + 1) \times \dfrac {2 ^2} {3 ^2}$ $\;\; = 1 - \dfrac 8 9 = \dfrac 1 9 = p_2 = S_2$

On a donc prouvé que $\mathcal{P}(2)$ est vraie.

$\bullet$ Hérédité

On suppose que $\mathcal{P}(n)$ est vraie.

$S_{n + 1} = S_n + p_{n + 1}$

$= 1 - \left ( \dfrac n 2 + 1 \right ) \times \dfrac {2 ^{n}} {3 ^n} + \dfrac {n} 4 \times \dfrac {2 ^{n+1 }} {3 ^{n + 1}}$

$= 1 - \left ( \dfrac n 2 \times\dfrac 3 2 + 1 \times \dfrac 3 2 - \dfrac {n } 4 \right ) \dfrac {2 ^{n+1 }} {3 ^{n + 1} }$

$S_{n + 1} = 1 - \left ( \dfrac n 2 + \dfrac {3} 2 \right ) \dfrac {2 ^{n+1}} {3 ^[n + 1}}$

$S_{n + 1} = 1 - \left ( \dfrac {n + 1} 2 + 1 \right ) \dfrac {2 ^{n+1}} {3 ^{n + 1}}$

On a donc prouvé $\mathcal{P}(n + 1)$ .

$\bullet$ Conclusion : la propriété est vraie au rang $n + 1$ .

b. $\bullet$ On détermine la limite de la suite $(n \, x ^n)_n$ lorsque $0 < x < 1$ .

On note $v_n = \ln(n \, x ^n) = \ln(n) + n \ln(x)$

$v_n = n \left ( \ln(x) + \dfrac {\ln(n)} n \right )$

avec $\displaystyle \lim_{n \to + \infty} \dfrac {\ln(n)} n = 0$ donc

$\displaystyle \lim_{n \to + \infty} \left ( \ln(x) + \dfrac {\ln(n)} n \right ) = \ln(x) < 0$

puis $\displaystyle \lim_{n \to + \infty} v_n = - \infty$

donc $\displaystyle \lim_{n \to + \infty} \textrm{e} ^{v_n} = 0$

soit $\displaystyle \lim_{n \to + \infty} u_n = 0$ .

$\bullet$ $\displaystyle \lim_{n \to + \infty} S_n = 1$ .

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

Correction exercice baccalauréat 2000 sur la Loi Binomiale

Question 1

$\mathbb{P}(R_1) = \mathbb{P} \left (R_1 \cap \overline{A_1} \right )$

$\mathbb{P}(R_1) =\mathbb{P} \left ( \overline{A_1} \right ) \times \mathbb{P} \left (R_1 \,\mid \, \overline{A_1} \right )$

$\mathbb{P}(R_1) = 0,6 \times 0,2 = 0,12$ .

Question 2

On utilise $\mathbb{P}(R_2) = \mathbb{P}(R_2 \cap \overline{A_2} \cap A_1)$

$\mathbb{P}(R_2) =$ $\;\ \mathbb{P}(A_1) \, \mathbb{P}(\overline{A_2}\,\mid A_1 )\, \mathbb{P}(R_2 \,\mid \, A_1 \cap \overline{A_2})$
$\mathbb{P}(R_2) = 0,4 \times 0,7 \times 0,2 = 0,056$ .

Puis comme $R = R_1 \cup R_2\,$ , les événements étant incompatibles,

$\mathbb{P}(R) = \mathbb{P}(R_1) + \mathbb{P}( R_2) = 0,12+ 0,056$
$\boxed{\mathbb{P}(R) = 0,176}$ .

Question 3

On demande maintenant $\mathbb{P}_R(R_1) = \dfrac {\mathbb{P}(R _ 1 \cap R)} {\mathbb{P}(R)} = \dfrac {\mathbb{P}(R _ 1)} {\mathbb{P}(R)} = \dfrac {0, 12} {0,176}$
$\mathbb{P}_R(R_1) = \dfrac {12} {176} = \boxed{\dfrac 3 {4 4}}$ .

Question 4

On répète 20 épreuves de Bernoulli indépendantes et identiques de probabilité de succès égale à $p = \mathbb{P}(R)$

On demande 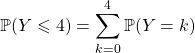$\mathbb{P}(Y \leqslant 4) = \displaystyle \sum _ {k = 0} ^4 \mathbb{P}(Y = k)$ $\displaystyle \mathbb{P}(Y \leqslant 4) = \sum _ {k = 0} ^4\binom {20} 4 \, p ^k \, (1 - p) ^{20-k}$
$\boxed{\mathbb{P}(Y \leqslant 4) \approx 0,7316}$ .

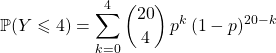
Correction de l’exercice sur le contrôle de production

Question 1

$X$ est le nombre de composants défectueux, $X$ suit une loi binomiale de paramètres $n = 10\, 000$ et $p = 0.002$ .
Le coût des contrôles est $0 ,1 \times n$ , le coût des destructions est $X$ .
Le coût est $Y = 0,1 \times n + X$ .
Le coût moyen est égal à

$\textrm{E}(Y) = 0,1 \times n + \textrm{E}(X)$

$\textrm{E}(Y) = 0,1 \times n + n\times p = n \, (0.1+ 0.002)$

$\textrm{E}(Y) = 10\, 000 \times 0.1002 = \boxed{1\,002 }$ €.

Question 2

Soit un lot de 10 donné.

La probabilité $q$ pour qu’il ne soit pas détruit est égale à $q = 0.998 ^{10}$ .
La probabilité qu’il soit détruit est égale à $1 - q \approx 0.019821$ .

Le nombre $Y$ de lots détruits suit une loi binomiale de paramètres $1000$ et $1 - q$
et le coût est égal à $\qquad \qquad Z = 1\,000 \times 0.1 + 10 \, Y$ .