Chapitres Maths en Terminale Générale
Exercices et corrigés : Les nombres complexes en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Se préparer au bac avec les exercices et les corrigés d’exercices sur le chapitre des nombres complexes au programme de maths en Terminale en option maths expertes. L’apprentissage des mathématiques ne sera efficace que s’il y a entraînement sur des exercices ou sur des annales de maths du bac. Ceci est d’autant plus vrai pour les cours de maths en option maths expertes. Le niveau y est très élevé et les exigences des professeurs le sont aussi. Pour être sûr de pouvoir suivre le rythme des cours, les élèves de terminale ont la possibilité de prendre des cours particuliers de maths et/ou de suivre des stages intensifs de révisions pendant les vacances scolaires.
1. Calcul sur les nombres complexes en Terminale, Maths Expertes
Exercices sur la forme cartésienne des nombres complexes
Calculer la forme cartésienne des complexes suivants :
Question 1 :
![]()
![]() ?
?
Question 2 :
![]()
![]() ?
?
Question 3 :
![]()
![]() ?
?
Question 4 :
![]()
![]() ?
?
Question 5 :
![]()
![]() ?
?
Exercice de calcul dans le plan complexe
Soit ![]() .
.
Déterminer l’ensemble des points ![]() d’affixe
d’affixe ![]() tels que
tels que ![]() soit réel,
soit réel,
puis l’ensemble des points ![]() d’affixe
d’affixe ![]() tels que
tels que ![]() soit imaginaire pur.
soit imaginaire pur.
Exercices de calcul sur les modules
Question 1 :
Résoudre ![]() .
.
Question 2 :
Ensemble des complexes ![]() tels que
tels que ![]() ,
, ![]() et
et ![]() aient même module.
aient même module.
Nombre de solutions ?
Exercices sur les équations des nombres complexes
Question 1 :
L’équation ![]()
admet une unique solution ![]() avec
avec ![]() ?
?
Question 2 :
L’équation ![]()
admet une unique solution ![]() avec
avec ![]() ?
?
Correction des exercices sur la forme cartésienne des nombres complexes
Question 1 :
![]()
![]() .
.
Question 2 :
En utilisant le binôme de Newton
![]()
![]()
![]()
![]()
![]() .
.
Question 3 :
En utilisant le binôme de Newton
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Question 4 :
![]()
![]()
![]()
![]() .
.
Question 5 :
![]()
![]()
![]()
![]()
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice de calcul dans le plan complexe
On cherche la forme cartésienne de ![]() .
.
![]() On suppose que
On suppose que ![]() avec
avec ![]() et
et ![]()
On écrit que ![]()
![]()
donc ![]()
![]() .
.
![]()
![]() ssi
ssi ![]()
ssi ![]() et
et ![]()
ssi ![]() est un point de l’axe des réels différent de
est un point de l’axe des réels différent de ![]() .
.
![]()
![]() est imaginaire pur
est imaginaire pur
ssi ![]()
ssi ![]() et
et ![]()
On écrit ![]()
![]() est imaginaire pur ssi
est imaginaire pur ssi ![]() et
et ![]()
ssi ![]() est un point du cercle de centre
est un point du cercle de centre ![]() et de rayon
et de rayon ![]() différent de
différent de ![]() .
.
Correction des exercices de calcul sur les modules
Question 1 :
On note ![]() où
où ![]() .
.
On résout donc ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]() ou
ou ![]()
L’ensemble des solutions est la réunion des deux ensembles :
![]()
![]() .
.
Question 2 :
Nombre de solutions : 2
![]()
![]() ssi
ssi ![]()
ssi ![]()
ssi ![]() ou
ou ![]() .
.
![]() Si
Si ![]() alors
alors ![]() donc
donc ![]() , les trois modules ne sont pas égaux.
, les trois modules ne sont pas égaux.
![]() Si
Si ![]() , on écrit
, on écrit ![]() avec
avec ![]() et
et ![]()
![]()
![]()
![]() ssi
ssi ![]() ssi
ssi ![]()
alors ![]() .
.
Il y a deux solutions
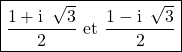 .
.
Correction des exercices sur les équations des nombres complexes
Question 1 :
![]() -19/170;-43/170
-19/170;-43/170
![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]() .
.
Question 2 :
![]() 4;5
4;5
![]()
On note ![]() avec
avec ![]() .
.
L’équation s’écrit
![]()
![]()
ssi ![]()
![]()
ssi ![]() .
.
En égalant parties réelles et imaginaires, on obtient le système
![]()
ssi ![]()
ssi ![]()
ssi ![]()
L’équation admet une unique solution ![]() .
.
2.Formes trigonométriques, nombres complexes :Terminale Maths Expertes
Exercices sur les modules et les arguments des nombres complexes
Question 1 :
Module et argument de ![]()
Question 2 :
a – Module et argument de ![]()
b – En déduire ![]() et
et ![]()
c – En déduire ![]() et
et ![]()
Exercices sur l’utilisation du plan complexe en Terminale
Dans ce paragraphe, on se place dans le plan complexe rapporté au repère orthonorma direct ![]() .
.
Soit ![]() un réel non nul. On note
un réel non nul. On note ![]() et
et ![]() les points du plan complexe d’affixes respectives
les points du plan complexe d’affixes respectives
![]() ,
, ![]() et
et ![]() .
.
Question 1 :
Calculer ![]() et
et ![]() .
.
Question 2 :
Trouver ![]() tel que le triangle soit isocèle en
tel que le triangle soit isocèle en ![]() .
.
![]() ?
?
Question 3 :
Existe-t-il un réel ![]() tel que le triangle
tel que le triangle ![]() soit équilatéral ?
soit équilatéral ?
Question 4 :
Donner les valeurs de ![]() tel que le triangle
tel que le triangle ![]() soit rectangle
soit rectangle
Question 5 :
Les points ![]() et
et ![]() sont alignés pour
sont alignés pour ![]() ?
?
Question 6 :
Déterminer l’affixe du point ![]() tel que
tel que ![]() soit un parallélogramme.
soit un parallélogramme.
Correction des exercices sur les modules et les arguments des nombres complexes
Question 1 :
En multipliant par la quantité conjuguée du dénominateur,
![]()
![]()
![]()
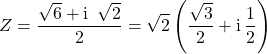
![]() est un complexe de module 1 et d’argument
est un complexe de module 1 et d’argument ![]() car
car
![]() et
et ![]() .
.
![]() et
et ![]() .
.
Question 2 :
a –
![]()
![]()
![]() , donc
, donc ![]()
Puis on cherche ![]() tel que
tel que
![]() et
et ![]()
on peut donc choisir ![]()
![]() .
.
![]()
![]()
![]() , donc
, donc ![]()
Puis on cherche ![]() tel que
tel que
![]() et
et ![]() .
.
On peut donc choisir ![]() .
.
![]() .
.
![]() alors si
alors si ![]()
![]() soit
soit ![]()
et ![]()
![]()
![]() .
.
b –
On cherche la forme cartésienne de ![]() :
:
![]()
![]()
On a trouvé la forme trigonométrique de ![]() :
:
![]()
donc en égalant les parties réelles et imaginaires
![]()
et ![]()
donc 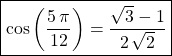 et
et 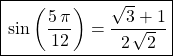 .
.
c –
Puis en utilisant ![]()
![]()
![]() et
et ![]() ,
,
![]()
![]()
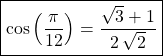
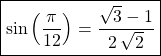 .
.
Correction des exercices sur l’utilisation du plan complexe en Terminale
Question 1 :
![]()
![]() .
.
![]()
![]() .
.
Question 2 :
![]() 1
1
![]() ssi
ssi ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
Question 3 :
Si ![]() ,
, ![]()
et ![]()
![]() .
.
Le triangle ne peut pas être équilatéral.
Question 4 :
![]() Le triangle est rectangle en
Le triangle est rectangle en ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
Cette équation n’a pas de racine réelle car ![]() .
.
![]() Le triangle est rectangle en
Le triangle est rectangle en ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]() .
.
![]() Le triangle est rectangle en
Le triangle est rectangle en ![]()
ssi ![]()
ssi ![]()
ssi ![]() ssi
ssi ![]() .
.
Le triangle est rectangle ssi ![]() ou
ou ![]() .
.
Question 5 :
![]() -3
-3
On calcule les affixes ![]() et
et ![]() de
de ![]() et
et ![]()
![]()
![]()
Il existe un réel ![]() tel que
tel que ![]() ssi
ssi ![]() ssi
ssi ![]() et
et ![]()
ssi ![]() et
et ![]() .
.
Les points sont alignés ssi ![]() .
.
Question 6 :
On suppose donc que ![]() et
et ![]() ne sont pas alignés c’est à dire
ne sont pas alignés c’est à dire ![]() .
.
![]() est un parallélogramme ssi
est un parallélogramme ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]()
ssi ![]() .
.
3. La trigonométrie et les nombres complexes en Terminale Maths Expertes
Exercices avec  etc … en Terminale
etc … en Terminale
Question 1 :
Pour tout réel ![]() ,
, ![]()
Vrai ou Faux ?
Question 2 :
Si ![]() , simplifier
, simplifier
![]() .
.
Exercices sur la formule de Moivre
Question 1 :
Soit ![]() . Exprimer
. Exprimer ![]() en fonction de
en fonction de ![]()
Question 2 :
En déduire la valeur de ![]() .
.
Exercice sur la linéarisation en Terminale
Résoudre l’équation
![]() .
.
Quelles sont les solutions de cette équation dans ![]() ?
?
Exercice sur la transformation de 
Soient ![]() tels que
tels que ![]() , il existe un réel
, il existe un réel ![]() tel que
tel que
![]()
![]()
Introduire le complexe ![]() et sa forme trigonométrique.
et sa forme trigonométrique.
Correction des exercices avec  etc … en Terminale
etc … en Terminale
Question 1 :
Vrai
![]()
![]()
![]()
![]()
Question 2 :
![]()
![]()
![]()
![]()
![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction des exercices sur la formule de Moivre
Question 1 :
![]() Première méthode :
Première méthode :
![]()
![]()
![]()
![]()
![]() Deuxième méthode :
Deuxième méthode :
![]()
par le binôme de Newton
![]()
![]()
![]()
![]()
![]()
en égalant les parties réelles
![]()
![]()
avec ![]()
![]()
![]()
après simplifications :
![]() .
.
Question 2 :
On pose ![]() ,
, ![]()
donc ![]() .
.
En posant ![]() alors
alors ![]() , on résout l’équation
, on résout l’équation ![]()
de discriminant ![]()
on a deux racines ![]()
![]() et
et ![]() .
.
comme ![]() ,
, ![]() , on doit éliminer la valeur
, on doit éliminer la valeur ![]() et donc
et donc ![]() .
.
Sachant que ![]() , on obtient
, on obtient 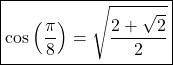 .
.
Correction de l’exercice sur la linéarisation en Terminale
![]()
![]()
![]()
![]()
![]()
L’équation est équivalente à
![]()
ssi ![]()
ou ![]()
ssi ![]()
ou ![]()
Si l’on cherche les solutions dans ![]() , ce sont les réels
, ce sont les réels
![]()
![]() .
.
Correction de l’exercice sur la transformation de 
![]() a pour module
a pour module ![]() et un argument
et un argument ![]() et donc
et donc ![]()
alors ![]() et
et ![]()
![]()
![]()
![]()
L’option maths expertes augmente le coefficient au bac de la spécialité maths, les élèves de terminale n’ont alors pas le droit à l’erreur. Tous les chapitres de maths doivent ainsi être parfaitement acquis pour réussir au bac. Par conséquent pour s’assurer d’être au niveau, les élèves peuvent s’aider des différents cours en ligne de maths au programme de l’option maths expertes :
- les équations polynomiales
- géométrie et complexes
- l’arithmétique – congruences
- l’arithmétique – PGCD PPCM
- arithmétique – nombres premiers et Fermat
Pour vérifier les notes à obtenir pour valider une mention les élèves peuvent utiliser le simulateur de bac. Si le travail des élèves durant l’année est sérieux et régulier, les résultats au bac seront au rendez-vous et les élèves pourront ainsi intégrer les meilleures écoles d’ingénieurs et de commerce ou les meilleures prepa HEC ou scientifiques.

