Chapitres du sous-test 2 du Tage Mage

Exercices corrigés théorème de Thales et sa réciproque

Enseigné au collège, le théorème de Thalès est un des théorèmes les plus important, au même titre que le théorème de Pythagore. Si il est impératif de maîtriser ce théorème pour préparer le brevet, cela ne sert à rien si on ne sait pas l’appliquer. S’exercer à pratiquer le théorème de Thalès dans le cadre d’une préparation au Tage Mage ou au Score IAE par exemple est donc fortement conseillé.

Fiche d’exercices sur le théorème de Thalès

Exercice 1 : Application directe du cours du théorème de Thalès

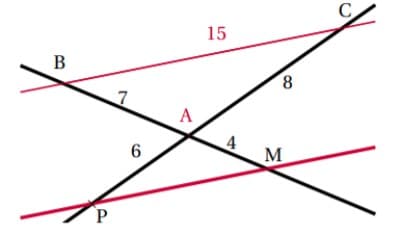
Dans la figure suivante, les droites (BM) et (PC) sont sécantes en A . On sait que :

AB = 7 cm ; AM = 4 cm ; AP = 6 cm ; AC = 8 cm

Les droites (BC) et (PM) sont-elles parallèles ?

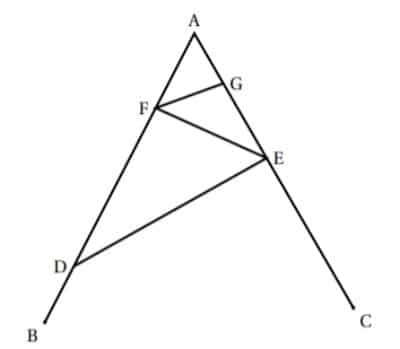
Exercice 2 : Une construction appliquant le théorème de Thalès

La figure ci-contre n’est pas en vraie grandeur. On donne les informations suivantes :

• Le triangle ADE a pour dimensions : AD = 7 cm, AE = 4,2 cm et DE = 5,6 cm.
• F est le point de [AD] tel que AF = 2,5 cm.
• B est le point de [AD) et C est le point de [AE) tels que : AB = AC = 9 cm.
• La droite (FG) est parallèle à la droite (DE).

Calculer la longueur FG.

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

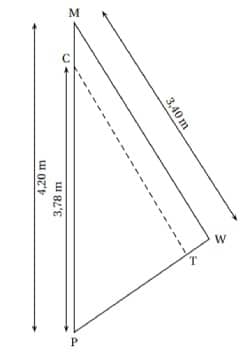
Exercice 3 : Le théorème de Thalès dans une voile

Un centre nautique souhaite effectuer une réparation sur une voile.

La voile a la forme du triangle PMW ci-dessous.

1. On souhaite faire une couture suivant le segment [CT].
1. a. Si (CT) est parallèle à (MW), quelle sera la longueur de cette couture ?
1. b. La quantité de fil nécessaire est le double de la longueur de la couture. Est-ce que 7 mètres de fil suffiront ?
2. Une fois la couture terminée, on mesure : PT = 1,88 m et PW = 2,30 m. La couture est-elle parallèle à (MW ) ?

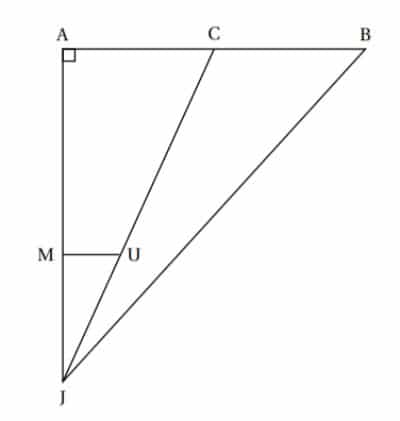
Exercice 4 : Le théorème de Thales et triangle rectangle

On considère la figure ci-dessous qui n’est pas à l’échelle.

Le triangle JAB est rectangle en A.
Les droites (MU) et (AB) sont parallèles.
Les points A, M et J sont alignés.
Les points C, U et J sont alignés.
Les points A, C et B sont alignés.
AB = 7,5 m.
MU = 3 m.
JM = 10 m.
JB = 19,5 m.
AJ = 18 m

Montrer que la longueur AC est égale à 5,4 m.

Exercices sur la réciproque du théorème de Thales

COURS A DOMICILE

Des cours sur mesure de qualité

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

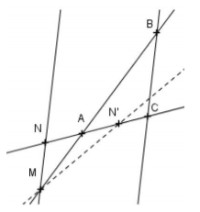
Exercice 1 : Le théorème de Thalès avec des triangles inversés

On considère la figure ci-contre pour laquelle :

AN = AN’= 2 cm, AM =3 cm, AB = 9 cm et AC = 6 cm.

Les droites (MN) et (BC) sont-elles parallèles ?

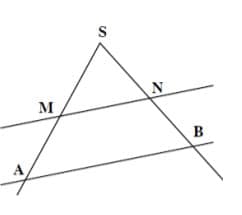
Exercice 2 : La réciproque du théorème de Thalès sur un triangle

On a SM = 4, SA = 12, SN = 6 et SN = 18

Les droites (AB) et (MN) sont-elles parallèles ?

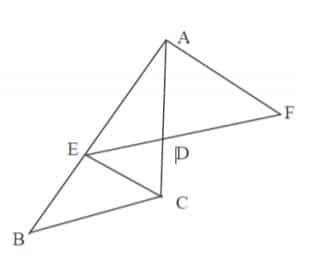
Exercice 3 : Réciproque du théorème de Thalès sur une figure quelconque

Soit ABC un triangle dans lequel on a tracé une droite (ED) parallèle à la droite (BC)

On a AE = BC = 3 et EB = AD = 2

1) Calculer AC, DC et ED

2) F est un point de (DE) tel que DF = 2,7

Déterminer si les droites (EC) et (AF) sont parallèles

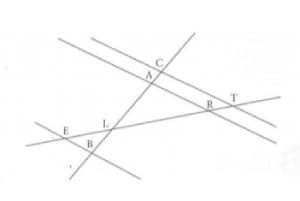
Exercice 4 : sur la réciproque du théorème de Thales

Sur la figure ci-contre

Les droites (AR) et (CT) sont parallèles.

Les points E, L, R, T et C, A, L, B sont alignés dans l’ordre respectif

On a également, LC = 6 ; LT = 9 ; LA = 4,8 ; LB = 1,5 et LE = 3
1) Calculer LR
2) Déterminer si les droites (EB) et (CT) sont parallèles

Tu veux réussir le brevet ?

Profite des meilleurs exercices et annales

Les meilleurs professeurs t'aideront individuellement

Prépare le lycée en maths, physique-chimie et français

99% de satisfaction lors de nos stages de préparation en 3eme au brevet

Avis Google France
★★★★★ 4,9 sur 5

Corrigés des exercices sur le théorème de Thales

Corrigé de l’exercice 1 : application du théorème de Thales

Dans la figure suivante, les droites (BM) et (PC) sont sécantes en A .

On sait que : B = 7 cm ; AM = 4 cm ; AP = 6 cm ; AC = 8 cm. Les droites (BC) et (PM) sont-elles parallèles

Données : Les points B, A, M et P, A, C sont alignés dans cet ordre sur deux droites sécantes en A.

D’une part : $\dfrac {AM}{AB}$ = $\dfrac {4}{7}$ = $\dfrac {16}{28}$

D’autre part : $\dfrac {AP}{AC}$ = $\dfrac {6}{8}$ = $\dfrac {3}{4}$ = $\dfrac {21}{28}$

Conclusion : On n’a donc pas égalité, $\dfrac {AM}{AB}$ $\neq$ $\dfrac {AP}{AC}$ . De ce fait, d’après la contraposée du théorème de Thalès, Les droites (BC) et (MP) ne sont pas parallèles.

Si vous avez des difficultés à comprendre cette correction ou à bien maitriser le théorème de Thales en 4ème et 3ème, n’hésitez pas à faire appel à un prof particulier de maths pour vous aider à pratiquer et comprendre le cours.

Corrigé de l’exercice 2 : construction avec le théorème de Thales

Données : Les points A, F, D et A, G et E sont alignés sur deux droites sécantes en A. Les droites (FG) et (DE) sont parallèles

Donc d’après le théorème de Thalès on a : $\dfrac{AF}{AD}$ = $\dfrac {AG}{AE}$ = $\dfrac {FG}{DE}$

Puis en remplaçant par les valeurs $\dfrac {2,5}{7}$ = $\dfrac {AG}{4,2}$ = $\dfrac {FG}{5,6}$

Calcul de FG : On a donc $\dfrac {2,5}{7}$ = $\dfrac {FG}{5,6}$

Puis FG = $\dfrac {2,5 \times 5,6}{7}$ = 2 cm

Corrigé de l’exercice 3 : théorème de Thalès dans une voile

On souhaite faire une couture suivant le segment [CT].

1. a. Si (CT) est parallèle à (MW), quelle sera la longueur de cette couture ?

Les points P, C, M et P, T, W sont alignés, et les droites (CT) et (MW) sont parallèles, on peut donc appliquer le théorème de Thalès,

$\dfrac {PC}{PM}$ = $\dfrac {CT}{MW}$

ou en remplaçant par les valeurs connues :

$\dfrac {3,78}{4,2}$ = $\dfrac {CT}{3,4}$

d’où :

CT = $\dfrac {3,78 \times 3,4}{4,2}$ = 3,06 m

1. b. La quantité de fil nécessaire est le double de la longueur de la couture. Est-ce que 7 mètres de fil suffiront?

3,06×2 = 6,12 < 7. Donc 7 m de fil suffiront.

2. Une fois la couture terminée, on mesure : P T = 1,88 m et PW = 2,30 m. La couture est-elle parallèle à (MW)?

Données : Les points P, C, M et P, T, W sont alignés dans cet ordre sur deux droites sécantes en P.

D’une part : $\dfrac {PC}{PM}$ = $\dfrac {3,78}{4,2}$ = 0,9

D’autre part part : $\dfrac {PT}{PW}$ = $\dfrac {1,88}{2,3}$ ≈ 0,8

Conclusion : On n’a donc pas égalité, $\dfrac {PC}{PM} \neq \dfrac {PT}{PW}$ .

De ce fait, d’après la contraposée du théorème de Thalès, Les droites (CT) et (MW) ne sont pas parallèles.

La couture n’a pas été faite parallèle au bord [MW] de la voile.

Corrigé de l’exercice 4 : théorème de Thalès appliqué à un triangle

Montrer que la longueur AC est égale à 5,4 m.

Dans le triangle JAC, les droites (MU) et (AC) sont parallèles, J, M et A sont alignés dans cet ordre, J, U et C sont alignés dans cet ordre : on peut donc appliquer le théorème de Thalès :

$\dfrac {JM}{JA} = \dfrac{JU}{JC} = \dfrac {MU}{AC}$

En particulier : $\dfrac {JM}{JA} = \dfrac {MU}{AC}$ donc $\dfrac {10}{18} = \dfrac {3}{AC}$

AC = $\dfrac {3 \times 18}{10}$ = 5,4 cm

Tu as besoin d'un soutien scolaire ?

Je révise en autonomie

Je progresse avec un prof à domicile

Je m’entraîne durant les vacances en petit groupe

Avis Google France
★★★★★ 4,9 sur 5

Corrigé sur la réciproque du théorème de Thales

Corrigé de l’exercice : avec des triangles inversés

On sait que les droites (MB) et (NC) sont sécantes en A. On peut alors calculer différents rapports

$\dfrac{AM}{AB}$ = $\dfrac{3}{9}$ = $\dfrac{1}{3}$

Et $\dfrac{AN}{AC}$ = $\dfrac{2}{6}$ = $\dfrac{1}{3}$

On en déduit que $\dfrac{AM}{AB}$ = $\dfrac{AN}{AC}$ = $\dfrac{1}{3}$

On sait également que les points M, A, B et N, A, C sont alignés dans l’ordre respectif

D’après la réciproque du théorème de Thalès, (MN) et (BC) sont parallèles.

Corrigé de l’exercice 2 : réciproque du théorème de Thalès sur un triangle

On compare les différents rapports dans le triangle,

$\dfrac{SM}{SA}$ = $\dfrac{4}{12}$ = $\dfrac{1}{3}$

$\dfrac{SN}{SB}$ = $\dfrac{6}{18}$ = $\dfrac{1}{3}$

On en déduit que $\dfrac{SM}{SA}$ = $\dfrac{SN}{SB}$

Dans le triangle ABS on a les points S, M, et A alignés dans le même ordre que les points S, N, et B

D’après la réciproque du théorème de Thalès, (MN) et (AB) sont parallèles.

Corrigé de l’exercice 3 : réciproque du théorème de Thalès sur une figure quelconque

1) Les points A, E et B sont alignés ainsi que les points A, D, et C. D’après le théorème de Thalès

$\dfrac {AE}{AB} = \dfrac {AD}{AC} = \dfrac {DE}{BC}$

Donc $\dfrac {3}{5} = \dfrac {2}{AC}$ d’où AC = $\dfrac {10}{3}$

Le point D appartenant à [AC] donc DC = $\dfrac {10}{3} - 2$ donc $DC = \dfrac {4}{3}$

$\dfrac {3}{5} = \dfrac {DE}{3}$

Donc $DE = \dfrac {9}{5}$

2) On compare les différents rapports dans le triangle,

$\dfrac {DF}{DE} = 2,7 \times \dfrac {5}{9} = 1,5$

$\dfrac {DA}{DC} = 2 \times \dfrac {3}{4} = 1,5$ donc $\dfrac {DA}{DC} = \dfrac {DF}{DE}$

Les points A, D et C et F, D et E sont alignés dans le même ordre et $\dfrac {DA}{DC} = \dfrac {DF}{DE}$

D’après la réciproque du théorème de Thalès, (EC) et (AF) sont parallèles.

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

Avis Google France ★★★★★ 4,8 sur 5

Corrigé de l’exercice 4 : la réciproque du théorème de Thalès

1) Les points L, A, et C sont alignés dans le même ordre que L, R, et T et (AR) et CT) sont parallèles.

Donc d’après le théorème de Thalès $\dfrac {LA}{LC} = \dfrac {LR}{LT} = \dfrac {AR}{CT}$

Donc $\dfrac {4,8}{6} = \dfrac {LR}{9} \iff LR = \dfrac {9 \times 4,8}{6}$

Donc $LR = 7,2$

2) on compare $\dfrac {LE}{LT}$ et $\dfrac {LB}{LC}$

$\dfrac {LE}{LT} = \dfrac {3}{9} = \dfrac {1}{3}$

$\dfrac {LB}{LC} = \dfrac {1,5}{3} = \dfrac {1}{2}$ donc $\dfrac {LE}{LT}$ est différent de $\dfrac {LB}{LC}$

Les points B, L, et C sont alignés dans le même ordre que les points E, L, et T

Mais $\dfrac {LE}{LT}$ n’est pas égal à $\dfrac {LB}{LC}$ , Donc d’après la réciproque du théorème de Thalès, (EB) et (CT) ne sont pas parallèles.

Comme vous avez pu le constater en traitant ces exercices, pour bien maîtriser le théorème de Thalès, il est nécessaire de maîtriser d’abord le cours sur les fractions. Toutes les notions de maths du sous-test 2 du Tage Mage sont complémentaires, il est donc plus qu’important de travailler sérieusement chaque notion, commencez par exemple, par revoir les chapitres suivants :

Exercices corrigés théorème de Thales et sa réciproque

Fiche d’exercices sur le théorème de Thalès

Exercice 1 : Application directe du cours du théorème de Thalès

Exercice 2 : Une construction appliquant le théorème de Thalès

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Exercice 3 : Le théorème de Thalès dans une voile

Exercice 4 : Le théorème de Thales et triangle rectangle

<img decoding="async" class="size-full wp-image-58414 aligncenter" src="https://groupe-reussite.fr/ressources/wp-content/uploads/2020/07/triangle-thales.jpg" alt="exercice theoreme thales" width="400" height="421" />

Exercices sur la réciproque du théorème de Thales

COURS A DOMICILE

Des cours sur mesure de qualité

POUR ACCÉLÉRER MA PROGRESSION

Exercice 1 : Le théorème de Thalès avec des triangles inversés

Exercice 2 : La réciproque du théorème de Thalès sur un triangle

<img decoding="async" class="size-full wp-image-58420 aligncenter" src="https://groupe-reussite.fr/ressources/wp-content/uploads/2020/07/pyramide-thales-exercice.jpg" alt="triangle exercice theoreme thales" width="242" height="215" />

Exercice 3 : Réciproque du théorème de Thalès sur une figure quelconque

<img decoding="async" class="size-full wp-image-58421 aligncenter" src="https://groupe-reussite.fr/ressources/wp-content/uploads/2020/07/thales-figure-quelquonque.jpg" alt="application thales avec figure quelconque" width="309" height="260" />

Exercice 4 : sur la réciproque du théorème de Thales

Tu veux réussir le brevet ?

Profite des meilleurs exercices et annales

Les meilleurs professeurs t'aideront individuellement

Prépare le lycée en maths, physique-chimie et français

Corrigés des exercices sur le théorème de Thales

Corrigé de l’exercice 1 : application du théorème de Thales

Corrigé de l’exercice 2 : construction avec le théorème de Thales

Corrigé de l’exercice 3 : théorème de Thalès dans une voile

Corrigé de l’exercice 4 : théorème de Thalès appliqué à un triangle

Tu as besoin d'un soutien scolaire ?

Je révise en autonomie

Je progresse avec un prof à domicile

Je m’entraîne durant les vacances en petit groupe

Corrigé sur la réciproque du théorème de Thales

Corrigé de l’exercice : avec des triangles inversés

Corrigé de l’exercice 2 : réciproque du théorème de Thalès sur un triangle

Corrigé de l’exercice 3 : réciproque du théorème de Thalès sur une figure quelconque

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

Corrigé de l’exercice 4 : la réciproque du théorème de Thalès

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales