Chapitres Maths en Terminale Générale
Exercices et corrigés : la loi des grands nombres
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Bien se préparer avec des exercices et corrigés sur le chapitre de la loi des grands nombres en terminale spécialité maths est essentiel pour bien réussir l’épreuve du bac.
1. Variables aléatoires en terminale spé Maths
Exercice 1 : l’espérance et la variance de variables aléatoires
3 enfants achètent un cornet de glace à une boule à leur marchand préféré : « Fanfan » à Aix les Bains.
10 parfums sont disponibles.
Question 1 :
Quelle est la loi du nombre ![]() de parfums choisis par les 3 enfants ?
de parfums choisis par les 3 enfants ?
Question 2 :
Calculer l’espérance et la variance de ![]() , donner les résultats sous forme décimale, séparés par un point virgule
, donner les résultats sous forme décimale, séparés par un point virgule
Deux enfants (une fille et un garçon) demandent maintenant chacun un cornet à 2 boules, les 2 boules peuvent être de même parfum et 10 parfums sont disponibles.
On note ![]() le nombre de parfums choisis.
le nombre de parfums choisis.
Question 3 :
Trouver la loi de ![]() .
.
Question 4 :
Donner une valeur approchée à ![]() près de l’espérance et la variance de
près de l’espérance et la variance de ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2 : Loi uniforme sur ![Rendered by QuickLaTeX.com [\![1 , n]\!]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2037%2018%22%3E%3C/svg%3E)
Question 1 :
On suppose que l’on tire au hasard un numéro entre ![]() et
et ![]() .
.
On note ![]() le nombre obtenu.
le nombre obtenu.
Déterminer la loi de ![]() .
.
On dit que ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() .
.
Calculer son espérance et sa variance.
On pourra utiliser 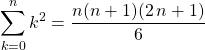 .
.
Question 2 :
On tire au hasard un deuxième numéro entre ![]() et
et ![]() .
.
On note ![]() la somme des deux numé- ros obtenus, déterminer l’espérance et la variance de
la somme des deux numé- ros obtenus, déterminer l’espérance et la variance de ![]() .
.
Question 3 :
On suppose dans cette question que ![]() .
.
Donner la loi de ![]() .
.
Question 4 :
Soient ![]() et
et ![]() deux entiers relatifs tels que
deux entiers relatifs tels que ![]() . On dit que
. On dit que ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() , lorsque
, lorsque
![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
a. Si ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() ,
, ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]()
b. En déduire l’espérance et la variance de ![]() .
.
2. Concentration, loi des grands nombres en terminale
Exercice 3 : Inégalités de Bienaymé-Tchebychev
On tire des boules avec remise dans une urne contenant ![]() de boules blanches.
de boules blanches.
Question 1 :
Quelle est la loi de la variable ![]() donnant le nombre de boules blanches obtenues après 20 tirages ?
donnant le nombre de boules blanches obtenues après 20 tirages ?
Question 2 :
a) En utilisant l’inégalité de Bienaymé-Tchebychev, donner une minoration de la probabilité de tirer moins de 16 boules blanches mais plus de 8.
b) Calculer ![]() , à
, à ![]() près, en utilisant la loi de
près, en utilisant la loi de ![]() et discuter la minoration obtenue dans la question précédente.
et discuter la minoration obtenue dans la question précédente.
Exercice 4 Inégalités de concentration
Quand nous pourrons voyager en avion sans problème …
Dans un avion, une personne est autorisée à mettre en soute un bagage de ![]() kg ou moins, sans pénalité.
kg ou moins, sans pénalité.
Une compagnie aérienne a compilé la masse de tous les bagages enregistrés sur une année et a constaté que la masse d’un bagage est donnée en kg par une variable aléatoire ![]() d’espé- rance 22 et d’écart-type 1,4.
d’espé- rance 22 et d’écart-type 1,4.
Question 1 :
Sur un avion de ![]() passagers suppo- sés indépendants, on appelle
passagers suppo- sés indépendants, on appelle ![]() la masse du bagage du passager
la masse du bagage du passager ![]() et
et ![]() la variable aléatoire donnant la moyenne des masses des bagages des
la variable aléatoire donnant la moyenne des masses des bagages des ![]() passagers.
passagers.
Minorer ![]() .
.
Question 2 :
Si la masse totale de bagages est inférieure ou égale à ![]() tonnes, alors l’avion embarque des bagages d’un autre vol et si la masse totale de bagages est supérieure ou égale à
tonnes, alors l’avion embarque des bagages d’un autre vol et si la masse totale de bagages est supérieure ou égale à ![]() tonnes, alors une partie des bagages de l’avion est envoyée sur un autre vol.
tonnes, alors une partie des bagages de l’avion est envoyée sur un autre vol.
Majorer la probabilité (à ![]() près) que cet avion contienne des bagages d’un autre vol ou ne contienne pas les bagages de tous ses passagers.
près) que cet avion contienne des bagages d’un autre vol ou ne contienne pas les bagages de tous ses passagers.
3. Les variables aléatoires pour se préparer à la prépa
Exercice 5 : Remplir des urnes selon les variables aléatoires
Soit ![]() . On répartit
. On répartit ![]() boules numérotées de
boules numérotées de ![]() à
à ![]() dans
dans ![]() urnes numérotées de
urnes numérotées de ![]() à
à ![]() .
.
Question 1 :
Si ![]() , on note
, on note ![]() la variable aléatoire égale à 1 si l’urne
la variable aléatoire égale à 1 si l’urne ![]() est vide et 0 si elle est non vide.
est vide et 0 si elle est non vide.
Quelle est la loi de ![]() ?
?
Question 2 :
On note ![]() le nombre d’urnes vides.
le nombre d’urnes vides.
Déterminer l’espérance de ![]() .
.
Question 3 :
Dans le cas ![]() , déterminer la loi de
, déterminer la loi de ![]() . Calculer sa variance.
. Calculer sa variance.
Question 4 :
On suppose de nouveau ![]() .
.
Si ![]() , on note
, on note ![]() si l’on place la boule
si l’on place la boule ![]() dans l’urne
dans l’urne ![]() .
.
On note ![]() la somme des numéros dans l’urne
la somme des numéros dans l’urne ![]() .
.
a. ![]() .
.
b. Déterminer ![]() et
et ![]() .
.
4. Correction des exercices sur la loi des grands nombres en terminale
Correction exercice sur la loi et variance de variable aléatoire de spé maths en terminale
Question 1 :
Il est conseillé de terminer par ![]()
![]() .
.
![]() Le nombre de choix possibles est égal au nombre de
Le nombre de choix possibles est égal au nombre de ![]() -listes avec répétition de l’ensemble
-listes avec répétition de l’ensemble ![]() des 10 parfums.
des 10 parfums.
Donc ![]() .
.
![]() Pour réaliser l’événement
Pour réaliser l’événement ![]() , il suffit de choisir le parfum plébiscité par les 3 enfants : il y a 10 choix de ce parfum, donc
, il suffit de choisir le parfum plébiscité par les 3 enfants : il y a 10 choix de ce parfum, donc ![]() .
.
alors ![]() .
.
![]() Pour réaliser l’événement
Pour réaliser l’événement ![]() , on doit choisir trois parfums différents.
, on doit choisir trois parfums différents.
C’est l’ensemble des ![]() – listes sans répétition des 10 parfums.
– listes sans répétition des 10 parfums.
![]() .
.
![]() .
.
![]() On peut donc tout simplement écrire que
On peut donc tout simplement écrire que
![]()
![]() .
.
Si l’on veut effectuer le calcul de ![]() ,
,
![]() On choisit le parfum demandé 2 fois : 10 choix
On choisit le parfum demandé 2 fois : 10 choix
![]() On choisit le parfum demandé 1 fois : 9 choix
On choisit le parfum demandé 1 fois : 9 choix
![]() On choisit l’enfant demandant ce parfum : 3
On choisit l’enfant demandant ce parfum : 3
alors ![]() et
et
![]()
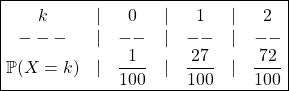
Question 2 :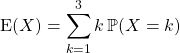
![]()
![]() .
.
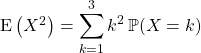
![]()
![]() .
.
![]()
![]() .
.
![]() .
.
Question 3 :![]() .
.
![]() On détermine le nombre de choix de parfums d’un enfant :
On détermine le nombre de choix de parfums d’un enfant :
![]() 10 choix du même parfum pour les deux boules
10 choix du même parfum pour les deux boules![]() choix de 2 parfums parmi 10 : nombre de parties de 2 éléments parmi 10
choix de 2 parfums parmi 10 : nombre de parties de 2 éléments parmi 10 ![]() .
.
Chaque enfant a donc ![]() choix pour ses parfums.
choix pour ses parfums.
![]()
![]()
![]()
et ![]()
![]() Calcul de
Calcul de ![]()
![]() La fille choisit ses 2 parfums parmi 10
La fille choisit ses 2 parfums parmi 10 ![]() choix
choix
![]() Le garçon choisit ses 2 parfums parmi 8 :
Le garçon choisit ses 2 parfums parmi 8 : ![]() choix
choix
donc ![]()
et ![]() .
.
![]() Calcul de
Calcul de ![]()
Un parfum est choisi deux fois, il peut être choisi par le même enfant ou par les deux enfants.
On écrit que ![]() avec :
avec :
![]()
![]() : « un enfant choisit 2 fois le même parfum et l’autre enfant choisit 2 autres parfums différents et différents du premier »
: « un enfant choisit 2 fois le même parfum et l’autre enfant choisit 2 autres parfums différents et différents du premier »
… On choisit l’enfant ayant un seul parfum : 2 choix
… On choisit ce parfum : 10 choix
… Le deuxième enfant choisit 2 parfums parmi 9 : ![]() choix
choix
![]() .
.
![]()
![]() : les deux enfants choisissent le même parfum et un deuxième parfum différent du premier et différent du deuxième parfum de l’autre »
: les deux enfants choisissent le même parfum et un deuxième parfum différent du premier et différent du deuxième parfum de l’autre »
… On choisit le parfum choisi 2 fois : 10 choix
… On choisit le 2 ème parfum de la fille : 9 choix
… On choisit le 2 ème parfum du garçon 8 choix
![]()
![]()
![]()
![]()
![]() La méthode la plus simple est d’écrire que
La méthode la plus simple est d’écrire que
![]()
![]()
![]()
![]() Si l’on veut faire le calcul de
Si l’on veut faire le calcul de ![]() , on écrit
, on écrit ![]() ,
,
![]()
![]() : « les deux enfants ont choisi les mêmes deux parfums «
: « les deux enfants ont choisi les mêmes deux parfums «
il y a ![]() choix de ces 2 parfums parmi 10
choix de ces 2 parfums parmi 10
donc ![]() .
.
![]()
![]() : » les deux enfants ont une glace d’un seul parfum et les 2 parfums sont distincts. »
: » les deux enfants ont une glace d’un seul parfum et les 2 parfums sont distincts. »
la fille a une glace à 2 boules de même parfum : 10 choix,
le garçon a une glace à 2 boules d’un même parfum différent du choix de la fille : 9 choix
donc ![]() .
.
![]()
![]() : « un parfum est choisi 3 fois et un dernier une fois »
: « un parfum est choisi 3 fois et un dernier une fois »
On choisit le parfum choisi 3 fois : 10 choix
on choisit le parfum choisi une fois : 9 choix
on choisit l’enfant prenant 2 parfums : 2 choix
donc ![]() .
.
![]()
![]()
![]() .
.
et on retrouve ![]() .
.
En résumé,
![]()
![]()
![]()
![]()
![]()
![]()
Question 4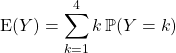
![]()
![]() .
.
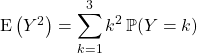
![]()
![]()
![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction exercice 2 : Loi uniforme sur ![Rendered by QuickLaTeX.com [\![1 , n]\!]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2037%2018%22%3E%3C/svg%3E) en terminale
en terminale
Question 1 :![]() Loi de
Loi de ![]()
![]()
Pour tout ![]() ,
, ![]() .
.
![]() Espérance
Espérance
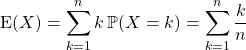
![]()
![]() .
.
![]() Calcul de la variance
Calcul de la variance
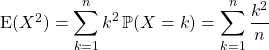
![]()
![]() .
.
![]()
![]()
![]()
![]()
Question 2 :
On note ![]() la variable aléatoire égale au deuxième numéro.
la variable aléatoire égale au deuxième numéro.
![]() .
.
Les variables ![]() et
et ![]() ont même loi et sont indépendantes,
ont même loi et sont indépendantes,
![]()
![]() .
.
![]()
![]() .
.
Question 3 :![]()
Soit ![]() ,
,
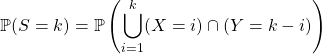
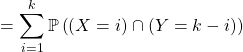
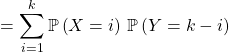
par indépendance de ![]() et
et ![]() .
.
avant de remplacer, il faut vérifier que ![]()
ssi ![]() et
et ![]()
on rappelle que ![]() , on distingue deux cas :
, on distingue deux cas :
![]()
![]() , les conditions précédentes s’écrivent
, les conditions précédentes s’écrivent ![]()
et ![]()
donc on obtient
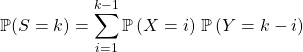
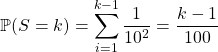
![]()
![]() , les conditions précéden- tes s’écrivent (on rappelle que
, les conditions précéden- tes s’écrivent (on rappelle que ![]() )
)
![]() et
et ![]()
donc on obtient
![]()
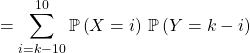
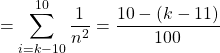
![]() .
.
En résumé,
Si ![]() ,
, ![]()
Si ![]() ,
, ![]() .
.
Question 4 :
a) ![]() prend toute valeur entière entre
prend toute valeur entière entre ![]() et
et ![]() ssi
ssi ![]() prend toute valeur entière entre
prend toute valeur entière entre ![]() et
et ![]() .
.
Et si ![]() ,
,
![]()
![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() avec
avec ![]() .
.
b) ![]() où
où ![]() suit une loi uniforme sur
suit une loi uniforme sur ![]() avec
avec ![]() .
.
![]()
![]() .
.
![]()
![]() .
.
Correction exercice 3 : Inégalités de Bienaymé-Tchebychev
Question 1 :
On effectue ![]() épreuves indépendantes et identiques de probabilité de succès égale à
épreuves indépendantes et identiques de probabilité de succès égale à ![]() .
.
Le nombre ![]() de boules blanches obtenues suit une loi binomiale de paramètres
de boules blanches obtenues suit une loi binomiale de paramètres ![]() et
et ![]() .
.
Question 2 :
a) ![]()
et ![]() .
.
![]()
![]()
![]()
![]()
En utilisant l’inégalité de Tchebychev,
![]() .
.
On termine l’application numérique :
![]()
donc ![]() .
.
b) 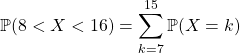
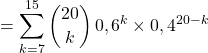
ma calculatrice préférée donne environ : ![]()
En Python, on peut utiliser la fonction Binomiale(n, p, a, b) écrite dans l’exercice 6
>>> Binomiale(20, 0.6, 9, 15)
0.893
L’inégalité de Bienaymé-Tchebychev donne en général une majoration ou minoration plus ou moins lointaine de la valeur exacte : elle ne prend pas en compte la loi de ![]() , seulement son espérance et sa variance.
, seulement son espérance et sa variance.
Correction exercice 4 : Inégalités de concentration
Question 1 :![]() est la moyenne empirique d’un échantillon de taille
est la moyenne empirique d’un échantillon de taille ![]() de variables aléatoires
de variables aléatoires ![]() de même loi que
de même loi que ![]() .
.
Soit ![]() avec
avec ![]() .
.
L’énoncé donne :![]() et
et ![]() .
.
On demande
![]()
![]()
![]()
![]()
Puis en utilisant l’inégalité de concentration,
![]()
On termine l’application numérique![]()
Question 2 :
La variable ![]() égale à la masse totale est
égale à la masse totale est ![]() .
.
On cherche à majorer la probabilité notée ![]() :
:
![]()
![]() en divisant par
en divisant par ![]()
![]()
Par l’identité de concentration
![]()
On passe à l’application numérique
![]()
La probabilité demandée est inférieure ou égale à ![]() , il y a donc peu de chances pour qu’il y ait des problèmes de bagages.
, il y a donc peu de chances pour qu’il y ait des problèmes de bagages.
Correction exercice 5 : Remplir des urnes selon les variables aléatoires
Question 1 :
Si ![]() , on note
, on note ![]() : « la boule numéro
: « la boule numéro ![]() n’est pas placée dans l’urne
n’est pas placée dans l’urne ![]() .
.
![]() .
.
Ce sont ![]() événements indépendants et
événements indépendants et ![]() .
.
donc ![]()
et ![]() .
.
Question 2 :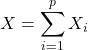 donc
donc 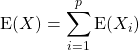
Les variables ont même loi :
![]() .
.
Question 3 :
On suppose dans cette question que ![]() .
.
On modélise ![]() par l’ensemble des
par l’ensemble des ![]() -listes avec répétition de
-listes avec répétition de ![]() (l’ensemble des numéros des 3 urnes) donc
(l’ensemble des numéros des 3 urnes) donc ![]() .
.
![]() et
et ![]() .
.
![]()
![]() est l’événement « toutes les boules sont mises dans la même urne «
est l’événement « toutes les boules sont mises dans la même urne «
![]() .
.
![]() .
.
![]()
![]() est l’événement « toutes les boules sont mises dans 2 urnes. »
est l’événement « toutes les boules sont mises dans 2 urnes. »
Pour réaliser ![]() ,
,
![]() on choisit les 2 numéros
on choisit les 2 numéros ![]() et
et ![]() des urnes non vides : il y a
des urnes non vides : il y a
![]() choix
choix
![]() on détermine le nombre de
on détermine le nombre de ![]() -listes avec répétition de
-listes avec répétition de ![]() , différentes des 2 listes dont tous les éléments sont égaux à
, différentes des 2 listes dont tous les éléments sont égaux à ![]() ou à
ou à ![]() : il y en a
: il y en a
![]() .
.
![]()
![]() .
.
Le calcul direct de ![]() est difficile, il est donc préférable de raisonner ainsi.
est difficile, il est donc préférable de raisonner ainsi.
![]()
![]()
![]()
![]() .
.
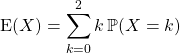
![]()
![]()
On retrouve bien la valeur obtenue en question 2 : ![]() .
.
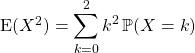
![]()
![]() .
.
![]()
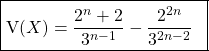 .
.
Question 4 :
a)La variable ![]() est nulle si le jeton
est nulle si le jeton ![]() n’est pas dans l’urne
n’est pas dans l’urne ![]() et égale à
et égale à ![]() si le jeton
si le jeton ![]() est dans l’urne
est dans l’urne ![]() .
.
donc ![]() est la variable aléatoire égale à la somme des numéros dans l’urne
est la variable aléatoire égale à la somme des numéros dans l’urne ![]() .
.
b) On rappelle que ![]() .
.
![]() Loi de
Loi de ![]()
![]() (car il y a
(car il y a ![]() choix d’urne pour le jeton
choix d’urne pour le jeton ![]() ).
).
![]() Calcul de
Calcul de ![]()
donc ![]() et
et ![]() par propriété des variables de Bernoulli.
par propriété des variables de Bernoulli.
Puis par linéarité de l’espérance,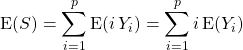
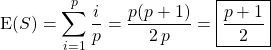 .
.
![]() Calcul de
Calcul de ![]()
Les variables ![]() sont indépendantes car associées à des épreuves indépendantes (mettre la boule numéro
sont indépendantes car associées à des épreuves indépendantes (mettre la boule numéro ![]() dans une des
dans une des ![]() urnes).
urnes).
Comme les variables ![]() sont indépendantes :
sont indépendantes :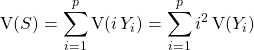
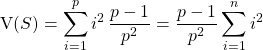
![]()
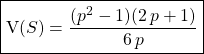 .
.

