Chapitres Maths en Terminale Générale

Cours, exercices & corrigés : la fonction exponentielle

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Résumé de cours sur la fonction exponentielle en Terminale :

Profitez de ce cours en ligne de terminale sur le chapitre des fonctions exponentielles au programme de maths en terminale. Les mathématiques sont une matière complexe qui nécessite d’être rigoureusement travaillée tout au long des années lycée. Le programme de seconde, tout comme le programme de 1ère, doit être parfaitement compris pour réussir à suivre celui de terminale. Ainsi, pour réussir en terminale, il faut être certain d’avoir correctement assimilé les chapitres des années précédentes, si ce n’est pas le cas, il est recommandé de prendre des cours particuliers de maths.

1.Définition et propriété : fonction exponentielle

Définition :

La fonction exponentielle est l’unique fonction $f$ , dérivable sur $\mathbb{R}$ , telle que :

$f'=f\text{ et }f(0)=1$

Propriété

La fonction exponentielle, notée $exp$ , vérifie :

$\boxed{\forall x,y \in \mathbb{R}\text{, }exp(x+y)=exp(x) \times exp(y)}$

et il existe un unique réel, noté $e$ ( $\approx 2.718$ ), tel que :

$exp(e)=1$

On démontre alors que la fonction exponentielle vérifie la notation suivante :

$\boxed{\forall x \in \mathbb{R}\text{, }exp(x)=e^{x}}$

Propriété : signe et variations

La fonction exponentielle est strictement positive sur $\mathbb{R}$ : $\forall x \in \mathbb{R}\text{, }e^{x}>0$ .

La fonction exponentielle est strictement croissante sur $\mathbb{R}$ . Donc, pour tous réels $x$ et $y$ :

$x < y \Longleftrightarrow e^{x} < e^{y}$

$x=y \Longleftrightarrow e^{x}=e^{y}$

Propriétés algébriques

Pour tous réels $x$ , $y$ et tout entier $n$ :

$e^{x+y}=e^{x} \times e^{y}$

$e^{-x}=\frac{1}{e^{x}}$

$e^{x-y}=\frac{e^{x}}{e^{y}}$

$e^{\frac{x}{2}}=\sqrt{e^{x}}$

$\left(e^{x}\right)^{n}=e^{nx}$

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

2. Limites et dérivée de la fonction exponentielle

Limites:

$\lim\limits_{x \longrightarrow +\infty} e^{x} = +\infty$

$\lim\limits_{x \longrightarrow -\infty} e^{x} = 0$

$\lim\limits_{x \longrightarrow +\infty} \frac{e^{x}}{x} = +\infty$

$\lim\limits_{x \longrightarrow -\infty} xe^{x} = 0$

On dit que la fonction exponentielle domine les fonctions polynomiales

$\lim\limits_{h \longrightarrow 0} \frac{e^{h}-1}{h} = 1$

Dérivée de la fonction exponentielle

La fonction exponentielle est dérivable (donc continue) sur $\mathbb{R}$ , et pour tout réel $x$ :

$\boxed{exp'(x)=exp(x)=e^{x}}$

L’approximation affine au voisinage de $0$ de la fonction exponentielle est $h \longrightarrow 1+h$ . On écrira :

$e^{h} \thicksim 1+h\text{, pour }h\text{ proche de }0$

Si $u$ est une fonction dérivable sur un intervalle $I$ , alors la fonction $e^{u}$ est dérivable sur $I$ et, pour tout $x$ de $I$ :

$\boxed{\left(e^{u}\right)'(x)=u'(x)e^{u(x)}}$

Tableau de variations et courbe

La tangente au point d’abscisse $0$ a pour équation : $y=x+1$ .

La tangente au point d’abscisse $1$ a pour équation : $y=ex$ (elle passe par l’origine).

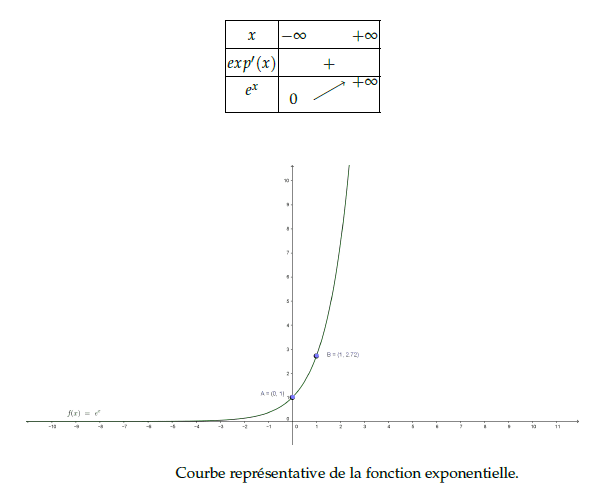
Résolution d’équations

Equation : $e^{x}=y$

Pour tout réel $y$ strictement positif, l’équation $e^{x}=y$ , d’inconnue $x$ , admet une unique solution dans $\mathbb{R}$ .

Exercices sur la fonction exponentielle

Exercice 1 :

Soit $f$ la fonction définie sur $\mathbb{R}$ par :

$f\text{ : }x \longmapsto x+2-\frac{4e^{x}}{e^{x}+3}$

On désigne par $C$ sa courbe représentative dans le plan rapporté à un repère orthonormé $(O;\overrightarrow{i};\overrightarrow{j})$ .

Question 1 :

Déterminer la limite de $f$ en $-\infty$ .

Question 2 :

Démontrer que la droite $D_{1}$ d’équation $y=x+2$ est asymptote à la courbe $C$ .

Question 3 :

Etudier la position de $C$ par rapport à $D_{1}$ .

Question 4 :

Justifier que $f$ est dérivable sur $\mathbb{R}$ , et calculer sa dérivée. Montrer que :

$\forall x \in \mathbb{R} \text{, }f'(x)=\left(\frac{e^{x}-3}{e^{x}+3}\right)^{2}$

Question 5 :

Etudier les variations de $f$ sur $\mathbb{R}$ et dresser son tableau de variations.

Question 6 :

Que peut-on dire de la tangente $D_{2}$ à la courbe $C$ au point $I$ d’abscisse $ln(3)$ ?

Question 7 :

En utilisant les variations de la fonction $f$ , étudier la position de la courbe $C$ par rapport à $D_{2}$ .

Question 8 :

Montrer que la tangente $D_{3}$ à la courbe $C$ au point d’abscisse $0$ a pour équation $y=\displaystyle {\frac{1}{4}}x+1$ .

Question 9 :

Etudier la position de la courbe $C$ par rapport à la tangente $D_{3}$ sur l’intervalle $]-\infty; ln(3)]$ .

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

Annales sur la fonction exponentielle en terminale générale

Rendez-vous sur les annales de maths au bac pour vous entraîner sur des dizaines d’exercices type bac. Les annales de bac sont un bon moyen de vérifier ses connaissances mais aussi de se familiariser avec les consignes et les attendus des vrais sujets d’examen. Le coefficient au bac pour les élèves ayant choisi la spécialité maths est très élevé. Les élèves de terminale sont invités à utilisez le simulateur de bac pour avoir une idée des notes à obtenir dans les différentes matières pour décrocher la mention.

Consultez aussi dès à présent les autres chapitres de maths au programme de Terminale pour booster votre moyenne :

Cours, exercices & corrigés : la fonction exponentielle

Résumé de cours sur la fonction exponentielle en Terminale :

1.Définition et propriété : fonction exponentielle

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

2. Limites et dérivée de la fonction exponentielle

Exercices sur la fonction exponentielle

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Annales sur la fonction exponentielle en terminale générale

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Cours, exercices & corrigés : la fonction exponentielle

Résumé de cours sur la fonction exponentielle en Terminale :

1.Définition et propriété : fonction exponentielle

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour réussir sa scolarité

En ligne ou à domicile

2. Limites et dérivée de la fonction exponentielle

Exercices sur la fonction exponentielle

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension clés de la réussite

Cours de maths en ligne ou à domicile

Annales sur la fonction exponentielle en terminale générale

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Les meilleurs profs de maths pour
réussir sa scolarité

La pratique et la compréhension
clés de la réussite