Chapitres Maths en Terminale Générale
Cours sur les fonctions logarithmes en Terminale
Résumé de cours : les fonctions logarithmes au programme de Terminale
Avec la réforme du bac, les programmes du lycée ont radicalement changé. Notamment en ce qui concerne le programme de maths en terminale qui est encore plus difficile que les années précédentes. Les notions sont plus nombreuses et les chapitres sont traités plus en profondeur. Pour s’assurer d’avoir de bons résultats au bac les élèves de terminale devront faire preuve de beaucoup de sérieux et devront fournir un grand travail personnel, car les mathématiques représentent un fort coefficient au bac, vous pouvez opter pour un prof de maths pour vous assurer la réussite au bac.
1. Définition de la fonction logarithme en Terminale
![]() Pour tout réel
Pour tout réel ![]() , il existe un unique réel
, il existe un unique réel ![]() tel que
tel que ![]() .
.
On note ![]() .
.
On définit ainsi une fonction appelée fonction logarithme (népérien) et notée
![]() .
.
![]() et
et ![]() ssi
ssi ![]() .
.
![]() Pour tout
Pour tout ![]() ,
, ![]() .
.
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]() .
.
On dit que les fonctions exponentielle et logarithme sont réciproques l’une de l’autre.
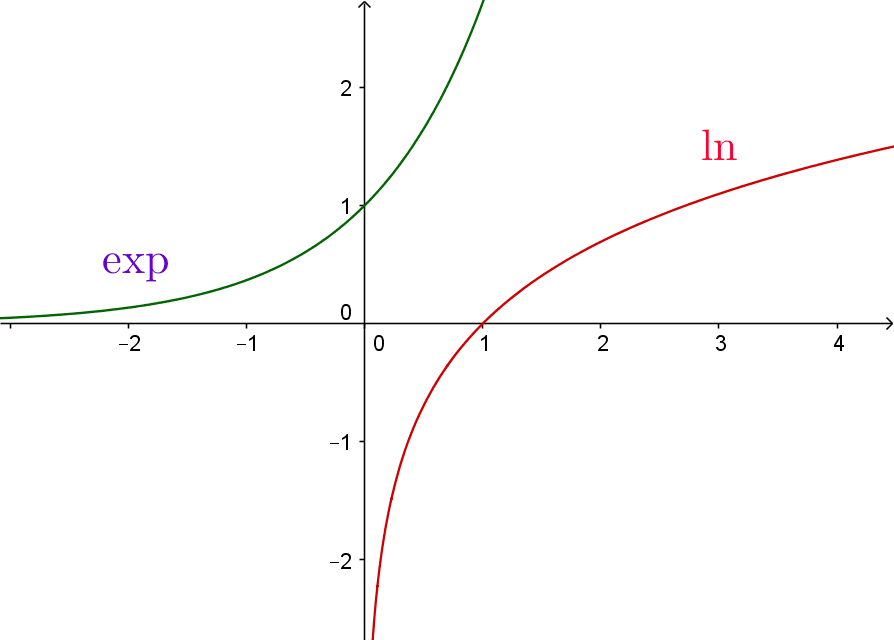
![]() Les graphes des fonctions exponentielle et logarithme sont symétriques par rapport à la droite d’équation
Les graphes des fonctions exponentielle et logarithme sont symétriques par rapport à la droite d’équation ![]() .
.
![]() (car
(car ![]() ) et
) et ![]() (car
(car ![]() )
)
On en déduit que la fonction ![]() est strictement croissante sur
est strictement croissante sur ![]()
car si ![]() ,
, ![]() et par stricte croissance de la fonction exponentielle :
et par stricte croissance de la fonction exponentielle : ![]() .
.
Si ![]() et
et ![]() ,
,
![]() ssi
ssi ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Propriétés algébriques de la fonction logarithme en Terminale
Soient ![]() et
et ![]() des réels strictement positifs.
des réels strictement positifs.
![]()
![]()
![]()
![]()
![]()
![]()
![]() si
si ![]() ,
, ![]() .
.
![]()
![]()
Avant d’écrire ![]() ,
,
vérifier que ![]() et
et ![]() .
.
Sinon, il faut écrire ![]() .
.
Même remarque pour la transformation de ![]() que vous écrirez bien sûr
que vous écrirez bien sûr ![]() si vous n’avez pas
si vous n’avez pas ![]() et
et ![]() .
.
Si ![]() ,
, ![]()
car ![]() !
!
3. Dérivée de logarithme en Terminale
![]() La fonction
La fonction ![]() est dérivable sur
est dérivable sur ![]() et si
et si ![]() ,
, ![]() .
.
Conséquence : la fonction ![]() est continue sur
est continue sur ![]() .
.
La démonstration à connaître :
On admet que la fonction ![]() est dérivable.
est dérivable.
La fonction ![]() est dérivable sur
est dérivable sur ![]() par composition
par composition
et si ![]() ,
, ![]()
Mais comme ![]() , on a aussi
, on a aussi ![]()
donc ![]() soit
soit ![]() .
.
![]() La fonction
La fonction ![]()
est dérivable et pour tout ![]() ,
, ![]() .
.
Pas de valeur absolue dans la dérivée !
Démonstration :
Sur ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() Si la fonction
Si la fonction ![]() est dérivable sur l’intervalle
est dérivable sur l’intervalle ![]() et ne s’annule pas, on peut définir
et ne s’annule pas, on peut définir ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
![]() La fonction
La fonction ![]() est concave sur
est concave sur ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
Ce qui peut aussi s’écrire, pour tout ![]() .
.
Démonstration :
![]() Une équation de la tangente en
Une équation de la tangente en ![]() est puisque
est puisque ![]() ,
, ![]() soit
soit ![]() .
.
Le graphe d’une fonction concave est situé sous toutes les tangentes,
Donc ![]() .
.
On obtient l’autre inégalité en remplaçant ![]() par
par ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
4. Les limites de fonctions logarithmes en Terminale
![]()
![]() .
.
![]()
![]() .
.
Démonstrations :
![]() Limite en
Limite en ![]() .
.
Par stricte croissance de la fonction ![]() ,
, ![]() donc
donc ![]() .
.
Soit ![]() et
et ![]() tel que
tel que ![]() ssi
ssi ![]() .
.
On note ![]() .
.
Si ![]() ,
, ![]()
soit ![]() donc
donc ![]() .
.
On a prouvé que l’intervalle ![]() contient tous les
contient tous les ![]() pour
pour ![]() assez grand, donc on a prouvé que
assez grand, donc on a prouvé que ![]() .
.
![]() Limite à droite en
Limite à droite en ![]() .
.
On pose ![]() , si
, si ![]() ,
, ![]()
et ![]() donc
donc
![]() .
.
![]()
![]()
![]()
![]() .
.
Démonstrations :
![]() Première limite
Première limite
![]() En utilisant le cours sur la fonction exponentielle.
En utilisant le cours sur la fonction exponentielle.
On note ![]() soit
soit ![]() .
.
Si ![]() ,
, ![]() .
.
![]() .
.
On sait que ![]() donc
donc ![]() .
.
![]() Sans utiliser le cours au programme de Première.
Sans utiliser le cours au programme de Première.
On note si ![]() ,
, ![]() .
.
![]() est dérivable et si
est dérivable et si ![]() ,
, ![]() .
.
![]() est croissante sur
est croissante sur ![]() avec
avec ![]()
donc si ![]() .
.
On applique cette inégalité en ![]() avec
avec ![]() :
: ![]()
et en divisant par ![]() :
:
![]() donc
donc ![]() .
.
Par encadrement par deux fonctions de limite nulle en ![]() , on déduit que
, on déduit que
![]() .
.
![]() Deuxième limite
Deuxième limite
On pose ![]() , si
, si ![]() ,
, ![]()
et ![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]()
et ![]() .
.
![]() Si
Si ![]() ,
, ![]()
et ![]() .
.
Démonstrations :
![]() Les limites en
Les limites en ![]() .
.
![]() Si
Si ![]() , il suffit d’écrire
, il suffit d’écrire ![]() ,
,
on obtient un produit de deux fonctions de limite nulle.
![]() En posant
En posant ![]() ,
, ![]() ,
,
on termine avec si ![]() ,
, ![]() .
.
![]() Les limites en
Les limites en ![]() .
.
![]() Si
Si ![]() , on écrit
, on écrit ![]()
et on a un produit de deux fonctions qui tendent vers 0.
![]() On pose
On pose ![]() (donc
(donc ![]() ). Si
). Si ![]() , il en est de même de
, il en est de même de ![]() .
.
![]() admet
admet ![]() pour limite à droite en
pour limite à droite en ![]() .
.
Un résultat utile à savoir démontrer
![]() .
.
Démonstration :
On introduit ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() et en reconnaissant un taux d’accroissement
et en reconnaissant un taux d’accroissement
![]()
![]()
car ![]() .
.
Profitez-en également pour consulter et vous exercer sur les annales de maths au bac, plus vous commencerez votre préparation au bac tôt, moins vous aurez à réviser la semaine précédant l’examen. Vous pourrez ainsi en profiter pour cibler vos révisions sur les notions qui vous posent des difficultés, notamment à l’aide des divers cours en ligne de maths au programme de terminale générale, comme :
- les fonctions trigonométriques
- le conditionnement et l’indépendance
- les primitives
- la dérivation et la convexité
- le calcul intégral
Pour être sûr d’obtenir les notes ciblées sur le simulateur du bac, il est vivement conseillé aux élèves de terminale de faire appel à un professeur particulier pour être accompagné pendant des cours particuliers de maths à domicile ou en ligne.

