Chapitres Maths en Terminale Générale
Géométrie dans l’espace en terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Résumé de cours : La géométrie dans l’espace au programme en Terminale
Le coefficient au bac des mathématiques pour ceux ayant pris la spécialité en Terminale est très élevé. Bien connaître toutes les notions au programme de maths en Terminale est donc indispensable pour réussir en Terminale. Ce cours et ces exercices corrigés sur la géométrie dans l’espace, vous permettront dans un premier temps, de revoir les définitions, les propriétés et les méthodes de calculs essentielles, puis d’identifier vos points forts et vos points faibles avec les exercices. Si vous rencontrez des difficultés, n’hésitez pas à prendre des cours particuliers de maths à Paris. Pour les élèves qui souhaitent une vraie remise à niveau ou qui souhaitent aller plus loin dans le programme de terminale, il est également possible de suivre des stages de révisions pendant les vacances scolaires.
1. Rappels sur le produit scalaire dans le plan
Définition :
On appelle produit scalaire de deux vecteurs ![]() et
et ![]() , le réel
, le réel ![]() défini par:
défini par:
![]() si aucun des deux vecteurs n’est nul
si aucun des deux vecteurs n’est nul
![]()
Autre expression du produit scalaire
Pour tous vecteurs ![]() et
et ![]() :
:
![]()
Dans un repère orthonormé, si les vecteurs ![]() et
et ![]() ont pour coordonnées respectives
ont pour coordonnées respectives ![]() et
et ![]() , alors:
, alors:
![]()
Propriétés
![]() Pour tous vecteurs
Pour tous vecteurs ![]() ,
, ![]() et
et ![]() et pour tous réels
et pour tous réels ![]() ,
, ![]() et
et ![]() :
:
![]()
(symétrie)
![]()
(multiplication par un scalaire)
![]()
(distributivité)}
![]() Soient
Soient ![]() et
et ![]() deux points distincts. Un point
deux points distincts. Un point ![]() vérifie
vérifie ![]() si et seulement si il appartient au cercle de diamètre
si et seulement si il appartient au cercle de diamètre ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Produit scalaire dans l’espace
Définition :
![]() Soient
Soient ![]() et
et ![]() des vecteurs non nuls, et
des vecteurs non nuls, et ![]() un point de l’espace. On note
un point de l’espace. On note ![]() et
et ![]() les points de l’espace tels que
les points de l’espace tels que ![]() et
et ![]() . Les points
. Les points ![]() ,
, ![]() et
et ![]() étant coplanaires, on définit le produit scalaire des vecteurs
étant coplanaires, on définit le produit scalaire des vecteurs ![]() et
et ![]() comme étant le produit scalaire des vecteurs
comme étant le produit scalaire des vecteurs ![]() et
et ![]() dans tout plan passant par
dans tout plan passant par ![]() ,
, ![]() et
et ![]() .
.
![]() Si
Si ![]() ou
ou ![]() est le vecteur nul, alors le produit scalaire
est le vecteur nul, alors le produit scalaire ![]() est nul.
est nul.
Règle fondamentale :
Toutes les propriétés du produit scalaire établies en géométrie plane sont valables dans l’espace, pour des points et des vecteurs coplanaires.
Expression du produit scalaire dans un repère orthonormal
Si l’espace est rapporté à un repère orthonormal ![]() , alors le produit scalaire des vecteurs
, alors le produit scalaire des vecteurs 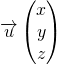 et
et 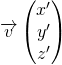 vérifie:
vérifie:
![]()
3. Représentation paramétrique d’une droite de l’espace
Soient ![]() et
et 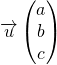 un vecteur non nul. La droite
un vecteur non nul. La droite ![]() passant par
passant par ![]() et de vecteur directeur
et de vecteur directeur ![]() est l’ensemble des points
est l’ensemble des points ![]() tels que:
tels que:
![]()
![]()
![Rendered by QuickLaTeX.com \[\left \{ \begin{array}{c @{=} c c} x-x_{0} \text{ }&\text{ } ka \\ y-y_{0} \text{ }&\text{ } kb & \text{ (avec $k \in \mathbb{R}$)}\\ z-z_{0} \text{ }&\text{ } kc \\ \end{array} \right.\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-a73fe492f873bb02cfb920f43115cbf6_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\left \{ \begin{array}{c @{=} c c} x \text{ }&\text{ } x_{0}+ka \\ y \text{ }&\text{ } y_{0}+kb & \text{ (avec $k \in \mathbb{R}$)}\\ z \text{ }&\text{ } z_{0}+kc \\ \end{array} \right.}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e62cad050eded45a297b2a96bc18bbea_l3.png)
Ce système est appelé une représentation paramétrique de la droite ![]() .
.
4. Equation cartésienne d’un plan
On se place dans un repère orthonormal ![]() .
.
![]() Soient
Soient ![]() un point de l’espace et
un point de l’espace et 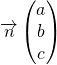 un vecteur non nul. Le plan passant par
un vecteur non nul. Le plan passant par ![]() et de vecteur normal
et de vecteur normal ![]() est l’ensemble des points
est l’ensemble des points ![]() tels que les vecteurs
tels que les vecteurs ![]() et
et ![]() soient orthogonaux, c’est-à-dire l’ensemble des points
soient orthogonaux, c’est-à-dire l’ensemble des points ![]() tels que:
tels que:
![]()
Les plans admettant 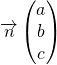 pour vecteur normal ont une équation cartésienne du type:
pour vecteur normal ont une équation cartésienne du type:
![]()
![]() Toute équation du type
Toute équation du type ![]() , où
, où ![]() ,
, ![]() ,
, ![]() et
et ![]() sont des réels non simultanément nuls, est une équation de plan, et
sont des réels non simultanément nuls, est une équation de plan, et 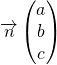 est un vecteur normal à ce plan.
est un vecteur normal à ce plan.
![]() Soient
Soient ![]() et
et ![]() le plan d’équation
le plan d’équation ![]() . La distance du point
. La distance du point ![]() au plan
au plan ![]() , notée
, notée ![]() , vérifie:
, vérifie:
![Rendered by QuickLaTeX.com \[\boxed{d(A,P) = \frac{|ax_{0}+by_{0}+cz_{0}+d|}{\sqrt{a^{2}+b^{2}+c^{2}}}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-55c838049c16b5120e31e73b1ec05b0f_l3.png)
4. Intersection de deux plans, d’une droite et d’un plan, de trois plans
Intersection de deux plans
Soient ![]() et
et ![]() deux plans de vecteurs normaux respectifs
deux plans de vecteurs normaux respectifs ![]() et
et ![]() .
.
![]() Si les vecteurs
Si les vecteurs ![]() et
et ![]() sont colinéaires, alors les plans
sont colinéaires, alors les plans ![]() et
et ![]() sont parallèles:
sont parallèles:
soit ![]() et
et ![]() sont strictement parallèles:
sont strictement parallèles: ![]()
soit ![]() et
et ![]() sont confondus:
sont confondus: ![]()
![]() Si les vecteurs
Si les vecteurs ![]() et
et ![]() ne sont pas colinéaires, alors les plans
ne sont pas colinéaires, alors les plans ![]() et
et ![]() sont sécants et leur intersection est une droite:
sont sécants et leur intersection est une droite:
![]()
Intersection d’une droite et d’un plan
Soient ![]() un plan de vecteur normal
un plan de vecteur normal ![]() et
et ![]() une droite de vecteur directeur
une droite de vecteur directeur ![]() .
.
![]() Si les vecteurs
Si les vecteurs ![]() et
et ![]() sont orthogonaux, alors la droite
sont orthogonaux, alors la droite ![]() est parallèle au plan
est parallèle au plan ![]() :
:
soit ![]() est strictement parallèle à
est strictement parallèle à ![]() :
: ![]()
soit ![]() est incluse dans
est incluse dans ![]() :
: ![]()
![]() Si les vecteurs
Si les vecteurs ![]() et
et ![]() ne sont pas orthogonaux, alors la droite
ne sont pas orthogonaux, alors la droite ![]() et le plan
et le plan ![]() sont sécants. Leur intersection est un singleton, c’est-à-dire un ensemble formé d’un seul point :
sont sécants. Leur intersection est un singleton, c’est-à-dire un ensemble formé d’un seul point :
![]()
Intersection de trois plans
L’intersection de trois plans est:
soit un singleton
soit une droite
soit un plan
soit l’ensemble vide
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
Exercices sur la géométrie dans l’espace en terminale :
Exercice 1 : Représentation paramétrique
On considère les points ![]() ,
, ![]() , et
, et ![]() .
.
Question 1 :
Donner une représentation paramétrique de la droite ![]() .
.
Question 2 :
Donner une représentation paramétrique de la demi-droite ![]() .
.
Question 3 :
Donner la représentation paramétrique du segment ![]()
Exercice 2 : Equation cartésienne du plan en terminale
Déterminer une équation cartésienne du plan ![]() défini par la condition suivante :
défini par la condition suivante :
Question 1 :
Le projeté orthogonal de l’origine ![]() sur
sur ![]() est le point
est le point ![]() .
.
Question 2 :
![]() passe par les points
passe par les points ![]() ,
, ![]() et
et ![]()
Question 3 :
![]() est le plan médiateur du segment
est le plan médiateur du segment ![]() , avec
, avec ![]() et
et ![]() (le plan médiateur d’un segment est le plan perpendiculaire à ce segment et qui passe par son milieu).
(le plan médiateur d’un segment est le plan perpendiculaire à ce segment et qui passe par son milieu).
Question 4 :
![]() est parallèle au plan
est parallèle au plan ![]() d’équation
d’équation ![]() , et passe par le point
, et passe par le point ![]()
Annales sur la géométrie dans l’espace en terminale
Entraînez-vous aussi sur les annales de maths au bac tout au long de l’année, c’est la clé de la réussite pour avoir de très bons résultats au bac. De plus, si vous visez la mention bien, voire la mention très bien au bac, utilisez aussi notre simulateur du bac afin d’avoir une idée des notes à obtenir pour décrocher cette mention. Plus vous vous entraînerez à travailler régulièrement dès le lycée, plus vous aurez de chance de réussir au sein des meilleures prépa scientifiques ou des meilleures prépa HEC.
Avant de vous tester en conditions réelles sur les annales du bac, vérifiez vos connaissances et travaillez vos points faibles sur les différents chapitres grâce aux cours en ligne de maths de terminale. Voici quelques chapitres à bien réviser :

