Chapitres Maths en Terminale Générale

La loi binomiale en Terminale Générale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1012 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

A. Épreuves indépendantes en Terminale

1. Définition des épreuves indépendantes en Terminale

Soit $n \in \mathbb{N}$ , $n \geqslant 2$ .

Soient $n$ épreuves $\mathcal{E}_i$ pour $i \in [\![1,\, n]\!]$ .

On note $\Omega_i$ l’univers (supposé fini) des résultats élémentaires associés à l’épreuve $\mathcal{E}_i$ et $\mathbb{P}$ la probabilité asso- ciée.

On note $\Omega = \Omega_1 \times \cdots \,\times \Omega_n$ l’univers associé à l’épreuve $\mathcal{E}$ formée par la succession des épreuves $\mathcal{E}_1\, , \, \cdots \,,\, \mathcal{E}_n \,$ .

Les épreuves sont indépendantes ssi la probabilité associée à l’épreuve $\mathcal{E}$ vérifie
pour tout $i \in [\![1,\, n]\!]$ , et tout $x_i \in \Omega_i\,$ ,

$\mathbb{P}\left (\{ (x_1\,,\, \cdots \,,\, x_n)\} \right ) =$ $\qquad \qquad \mathbb{P}\left (\{ x_1\} \right) \times \cdots \times \mathbb{P}\left (\{ x_n\} \right )$ .

Dans ce cas, si pour tout $i \in [\![1,\, n]\!]$ , $A_i \subset \Omega_i\,$ ,

$\mathbb{P}\left (A_1\,\times \, \cdots \, \times \, A_n \right ) =$ $\qquad \qquad \quad \mathbb{P}\left (A_1\right) \times \cdots \times \mathbb{P}\left (A_n\right )$ .

N’hésitez pas à prendre des cours particuliers de maths en cas de difficulté lors de ce chapitre.

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

2. Exemples d’épreuves indépendantes

Les épreuves « jeter un dé » puis « tirer une boule dans une urne » sont des épreuves indépendantes.

Les épreuves « jeter un dé » puis tirer une boule dans une urne portant le numéro donné par le dé » ne sont pas des épreuves indépendantes (sauf si les urnes ont la même composition ! ).

Les épreuves « jeter $n$ fois un dé » sont indépendantes.

Les épreuves « tirer $n$ fois une boule dans une urne »
… sont indépendantes lorsque l’on remet la boule à l’issue de chaque tirage
… ne sont pas indépendantes si la boule n’est pas remise après chaque tirage.

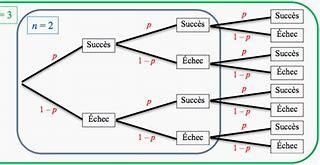
3. Utilisation d’un arbre

On peut lorsque le nombre d’épreuves $n$ est faible et le nombre de résultats possibles à chaque épreuve est faible, s’aider d’un arbre de probabilité.

B. Schéma de Bernoulli en Terminale

1. Épreuve de Bernoulli en Terminale

On dit qu’une épreuve est une épreuve de Bernoulli lorsqu’elle mène à la réalisation de deux événements $S$ (appelé succès) et $\overline{S}$ (appelé échec).

2. Variable aléatoire de Bernoulli en Terminale

$\bullet$ À une épreuve de Bernoulli, on peut associer la variable aléatoire $X$ définie par $X = 1$ si $S$ est réalisé et $X = 0$ si $S$ n’est pas réalisé.

$\bullet$ On note $p = \mathbb{P}(S)$ , alors la loi de $X$ est donnée par $X(\Omega) =\{0,\,1\}$ et $\mathbb{P}(X = 1) = p$ et $\mathbb{P}(X = 0) = 1 - p$ .

On dit que $X$ suit une loi de Bernoulli de paramètre $p$ et on note $X \hookrightarrow \mathcal{B}(p)$ .

$\bullet$ Réciproquement, si $X$ est une variable aléatoire dont la loi est définie par $X(\Omega) = \{0 ,\, 1\}$ et $\mathbb{P}(X = 1) = p$ et $\mathbb{P}(X = 0) = 1 - p$ , $X$ est la variable aléatoire de Bernoulli associée à l’épreuve de Bernoulli telle que $\quad S = (X = 1)$ et $\overline {S} = (X = 0)$ .

$\bullet$ Si $X \hookrightarrow \mathcal{B}(p)$ ,

$\textrm{E}(X) = p$ et $\textrm{V}(X) = p(1 - p)$ .

3. Schéma de Bernoulli

Soit $n \in \mathbb{N}^*$ , on dit que l’on a un schéma de Bernoulli lorsque l’on répète $n$ épreuves de Bernoulli identiques et indépendantes.

Lorsque l’on tire un échantillon de $n$ éléments dans une population très grande, sans remise, on n’a pas un schéma de Bernoulli, mais on pourra approcher l’ensemble des $n$ tirages par un schéma de Bernoulli.

C. Variable aléatoire binomiale en Terminale

1. Définition d’une variable aléatoire binomiale en Terminale

On considère une épreuve de Bernoulli dont la probabilité du succès est $p$ . On répète $n$ fois de façon indépendante cette épreuve et on note $X$ la variable aléatoire représentant le nombre de succès à l’issue de cette succession d’épreuves.

$X$ suit une loi binomiale de paramètres $n$ et $p$ et on note $X\hookrightarrow{B}(n , p)$ .

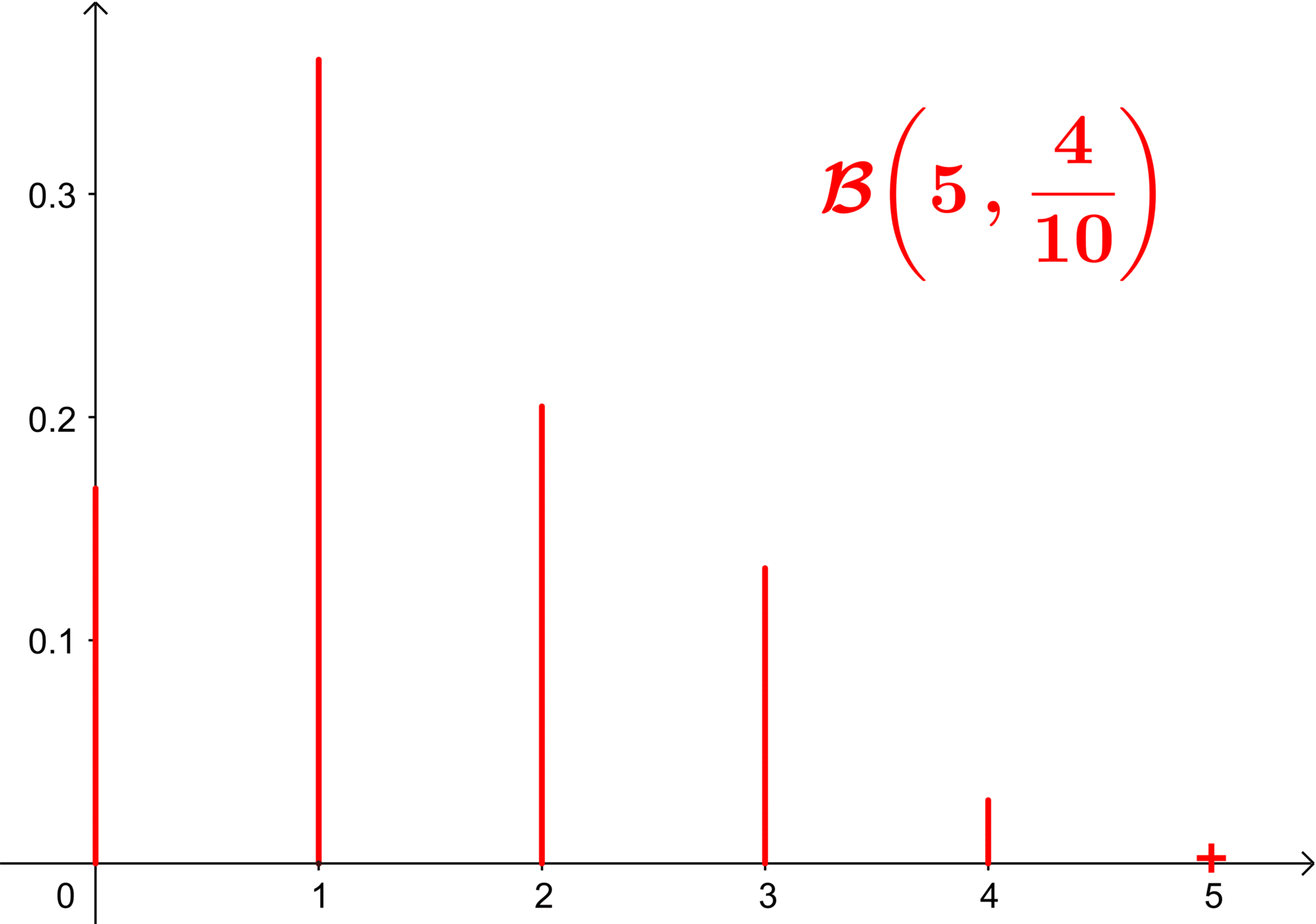
2. Formule de la loi binomiale

$\bullet$ Soit $n \in \mathbb{N}^*$ et $p \in\; ]0 , 1[$ , si $X$ suit une loi binomiale de paramètres $n$ et $p$ ,

$\ast$ $X(\Omega) = [\![0,\, n]\!]$ ,

$\ast$ pour tout $k \in [\![0,\, n]\!]$ , $\quad \mathbb{P}(X = k) = \displaystyle \binom n k \, p ^k \, (1 - p) ^{n - k}$ .

3. Espérance et variance de la loi binomiale

Si $X$ suit une loi binomiale de paramètres $n$ et $p$ ,

$\textrm{E}(X) = n \, p$ et $\textrm{V}(X) = n\, p\, (1 - p)$ .

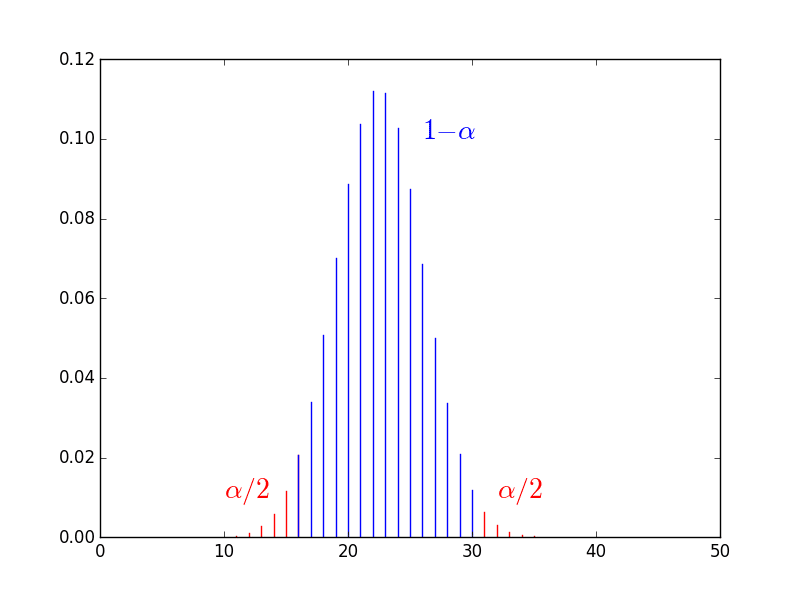
4. Intervalle de fluctuation de la loi binomiale

Soit $X$ une variable aléatoire de loi $\mathcal{B}(n , p)$ et $\alpha \in \; ]0 , 1[$ .

$\bullet$ Il existe deux entiers $a$ et $b$ tels que $\mathbb{P}(a \leqslant X \leqslant b ) \geqslant 1 - \alpha$ .

On dit que $[\![a ,\, b]\!]$ est un intervalle de fluctuation pour $X$ au risque $\alpha$ ou au seuil $1 - \alpha$

En pratique, on cherche le plus grand entier $a$ et le plus petit entier $b$ tels que $\mathbb{P}(a \leqslant X \leqslant b ) \geqslant 1 - \alpha$ .

$\bullet$ Si l’on impose : $a$ est le plus grand entier tel que $\mathbb{P} ( X < a ) \leqslant \dfrac \alpha 2$ et $b$ le plus petit entier tel que $\mathbb{P} ( X > b ) \leqslant \dfrac \alpha 2$ ,
alors $\mathbb{P}(a \leqslant X \leqslant b ) \geqslant 1 - \alpha$ .

On dit que l‘intervalle de fluctuation est centré.

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

D. Utilisation de Python pour modéliser la loi binomiale

1. Déterminer la loi d’une variable aléatoire binomiale

$\bullet$ La loi
from math import factorial as fact

def binom(n, p, k):
$\quad\vert$ return fact(n)/fact(k)/fact(n $-$ k)
$\quad \quad \quad$ * p **k * (1 $-$ p) **(n $-$ k)

$\bullet$ Calcul des probabilités cumulées :
pour obtenir 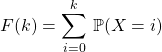$F(k) = \displaystyle \sum _ {i = 0} ^k \, \mathbb{P}(X = i)$

def cumulbinom(n, p, k):
$\quad\vert$ S = 0
$\quad\vert$ for i in range(k + 1):
$\quad\quad\vert$ S = S + binom(n, p, i)
$\quad\vert$ return S

$\bullet$ Pour obtenir la liste des $F(k)$ pour $0 \leqslant k \leqslant n$ :
def TablCumul(n, p):
$\quad\vert$ T=[] $\quad\vert$ S = 0
$\quad\vert$ for k in range (n + 1):
$\quad \quad \vert$ S= S +binom(n, p, k)
$\quad \quad \vert$ T.append(S)
$\quad\vert$ return T

Toutes ces fonctions ne sont utilisables que pour $n \leqslant 170$ .

2. Graphique de loi binomiale avec Python

Dans les deux cas :
import matplotlib.pyplot as plt

$\bullet$ Diagramme en bâtons de la loi d’une variable de Bernoulli (en rouge)
def batons(n,p):
$\quad\vert$ for k in range(0 , n + 1):
$\quad \quad \vert$ plt.plot([k, k],
$\qquad \qquad \quad$ [0 , binom(n , p, k) ], ‘r’)
$\quad\vert$ plt.show()

$\bullet$ En utilisant « bar »
remplacer $n$ et $p$ par leurs valeurs :
$\ast$ Déterminer dans une liste la loi de $X$
loi = [binom(n,p,k) for k in range(n + 1)] $\ast$ et utilisation de bar ;
plt.bar(range(n +1 ), loi, width = 0.1)

3. Simuler un tirage de Bernoulli, binomial, avec Python

Dans tous les cas,
import random

$\bullet$ Simulation d’une loi de Bernoulli :
def SimulBernoulli(p):
$\quad\vert$ a = random.random()
$\quad\vert$ if a < p:
$\quad \quad \vert$ return 1
$\quad\vert$ else:
$\quad \quad \vert$ return 0

et pour obtenir 20 simulations d’une loi de Bernoulli de paramètre $0.8$
[SimulBernoulli(0.8) for k in range (20)]

$\bullet$ Simulation d’une loi binomiale
def SimulBinomiale(n,p):
$\quad\vert$ res = 0
$\quad\vert$ for k in range (n):
$\quad \quad \vert$ if SimulBernoulli(p) == 1:
$\quad \quad \quad \vert$ res = res + 1
$\quad\vert$ return(res)

et pour obtenir 20 simulations d’une loi binomiale de paramètres 10 et $0.5$
[SimulBinomiale(10,0.5) for k in range (20)]

$\bullet$ Répétition de $Nbe$ simulations d’une loi binomiale
def RepeteSimulBinomiale(n, p, Nbe):
$\quad\vert$ L = [0]*(n + 1)
$\quad\vert$ for k in range(Nfois):
$\quad \quad \vert$ res = SimulBinomiale(n, p)
$\quad \quad \vert$ L[res] = L[res] + 1
$\quad\vert$ return(L)

et pour obtenir 20 simulations d’une loi binomiale de paramètres 10 et $0.4$ , suivies de la représentation :
LL= RepeteSimulBinomiale(10, 0.4, 20)
plt.bar(range(11 ), LL, width = 0.1)

$\bullet$ Calcul des fréquences des occurrences lors de $Nbe$ simulations d’une loi binomiale de paramètres $n$ et $p$
def FrequenceSimulBinomiale(n,p, Nbe):
$\quad\vert$ L = [0]*(n + 1)
$\quad\vert$ for k in range(Nbe):
$\quad \quad \vert$ res = SimulBinomiale(n, p)
$\quad \quad \vert$ L[res] = L[res] + 1
$\quad\vert$ for k in range(n + 1):
$\quad \quad \vert$ L[k] = L[k] /Nbe
$\quad\vert$ return(L)

et exemple de représentation (10000 simulations) :
F = FrequenceSimulBinomiale(10,0.4,10000)
plt.bar(range(11 ), F, width = 0.1)

4. Problèmes de seuils avec une variable X de loi binomiale

$\bullet$ Procédure qui donne le plus grand entier $k$ tel que $\mathbb{P} (X \leqslant k ) \leqslant \alpha$ :

def SeuilGauche(n, p, alpha):
$\quad\vert$ S = binom(n, p, 0)
$\quad\vert$ k = 0
$\quad\vert$ while S <= alpha:
$\quad\quad\vert$ k = k + 1
$\quad\quad\vert$ S = S + binom(n, p, k)
$\quad\vert$ return k $-$ 1

$\bullet$ Procédure qui donne le plus petit entier $k$ tel que $\mathbb{P}(X \geqslant k ) \leqslant \alpha$ :

def SeuilDroit(n, p, alpha):
$\quad\vert$ S = binom(n, p, n)
$\quad\vert$ k = n
$\quad\vert$ while S <= alpha:
$\quad \quad \vert$ k = k – 1
$\quad \quad \vert$ S = S + binom(n, p, k)
$\quad\vert$ return k + 1

$\bullet$ Procédure qui donne l’intervalle de fluctuation centré de $X$ au seuil de risque $\alpha$ :

def IntervalleFluc(n, p, risque):
$\quad\vert$ m = SeuilGauche(n, p, risque/2)
$\quad\vert$ M = SeuilDroit(n, p, risque/2)
$\quad\vert$ return [m+1, M $-$ 1]

Voici quelques autres chapitres de Mathématiques de Terminale, à connaître aussi pour réussir son Bac :

La loi binomiale en Terminale Générale

A. Épreuves indépendantes en Terminale