Chapitres Maths en Terminale Générale
Loi Normale, intervalle de fluctuation et estimation en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Résumé de cours Probabilités: Loi normale, fluctuation & estimation
Profitez de ce cours en ligne sur la loi normale, la fluctuation et les estimations au programme de maths de terminale pour vous remettre à niveau ou tout simplement pour contrôler vos connaissances sur le chapitre. Les élèves ayant sélectionné la spécialité maths au programme de Terminale doivent travailler dur, car le coefficient au bac, des mathématiques est très élevé. Pour définir les notes minimales à avoir au bac pour décrocher la mention bien ou la mention très bien, rendez-vous sur notre simulateur de bac et nos cours de maths particulier.
1. Loi normale
Définition: variable aléatoire centrée et réduite
On dit qu’une variable aléatoire est centrée et réduite lorsque son espérance est nulle et son écart-type égal à ![]() .
.
Propriétés
Soit ![]() une variable aléatoire prenant un nombre fini de valeurs, d’espérance
une variable aléatoire prenant un nombre fini de valeurs, d’espérance ![]() , de variance
, de variance ![]() et d’écart-type
et d’écart-type ![]() non nul.
non nul.
![]() La variable aléatoire
La variable aléatoire ![]() a une espérance nulle;
a une espérance nulle;
![]() La variable aléatoire
La variable aléatoire 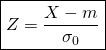 est une variable aléatoire centrée et réduite.
est une variable aléatoire centrée et réduite.
Théorème de Moivre-Laplace
Soit ![]() un nombre réel de l’intervalle
un nombre réel de l’intervalle ![]() .
.
Soit une suite de variables aléatoires ![]() où chaque variable aléatoire
où chaque variable aléatoire ![]() suit la loi binomiale
suit la loi binomiale ![]() .
.
On pose 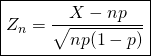 la variable aléatoire centrée et réduite associée à
la variable aléatoire centrée et réduite associée à ![]() .
.
Alors, pour tous réels ![]() et
et ![]() tels que
tels que ![]() , on a:
, on a:
![]()
![Rendered by QuickLaTeX.com \[= \int_{a}^{b} \frac{1}{\sqrt{2\pi}} e^{-\displaystyle{\frac{x^{2}}{2}}\text{ } dx}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-cab88c79c6244855017f9449750efef6_l3.png)
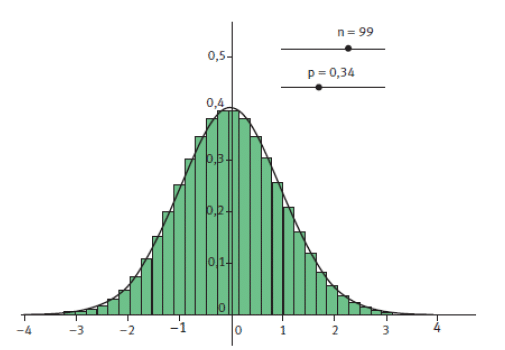
Représentation graphique de la loi de probabilité de la variable aléatoire ![]() (
(![]() ) et de la fonction
) et de la fonction 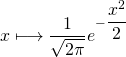
Les aires des rectangles représentent les probabilités. Le paramètre ![]() étant fixé, plus l’entier
étant fixé, plus l’entier ![]() augmente, plus la loi de probabilité de la variable aléatoire
augmente, plus la loi de probabilité de la variable aléatoire ![]() se rapproche de la loi de densité de probabilité
se rapproche de la loi de densité de probabilité 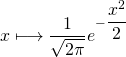 .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Loi normale centrée réduite 
Propriété
La fonction définie sur ![]() par
par 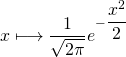 est une densité de probabilité.
est une densité de probabilité.
Définition
Une variable aléatoire à densité ![]() suit la loi normale centrée réduite
suit la loi normale centrée réduite ![]() si sa fonction de densité est la fonction définie sur
si sa fonction de densité est la fonction définie sur ![]() par
par
![Rendered by QuickLaTeX.com \[\boxed{f\text{ : }x \in \mathbb{R} \longmapsto \displaystyle{\frac{1}{\sqrt{2\pi}}} e^{-\displaystyle{\frac{x^{2}}{2}}}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-e8e7cca719e982c76f4a092503d39ff3_l3.png)
On a alors, pour tous réels ![]() et
et ![]() tels que
tels que ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[= \int_{a}^{b} \displaystyle{\frac{1}{\sqrt{2\pi}}} e^{-\displaystyle{\frac{x^{2}}{2}}}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-0d77b2c5e646685a50ffabd6bf50cd05_l3.png)
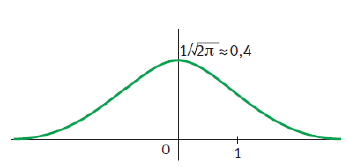
Courbe de Gauss – représentation graphique de la densité de probabilité 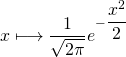
Propriétés
Soit ![]() une variable aléatoire à densité qui suit la loi normale centrée réduite
une variable aléatoire à densité qui suit la loi normale centrée réduite ![]() . On a:
. On a:
![]() Pour tout réel
Pour tout réel ![]() positif,
positif, ![]() ;
;
![]()
![]()
Définition: espérance de la loi normale centrée réduite
Si la variable aléatoire ![]() suit la loi normale centrée réduite
suit la loi normale centrée réduite ![]() , son espérance
, son espérance ![]() est définie par:
est définie par:
![]()
![]()
où ![]() est la fonction de densité de la loi normale centrée réduite
est la fonction de densité de la loi normale centrée réduite ![]() .
.
Propriété: espérance de la loi normale centrée réduite
L’espérance (ou la moyenne) de la loi normale centrée réduite ![]() est égale à
est égale à ![]() .
.
Propriété: variance de la loi normale centrée réduite
La variance de la loi normale centrée réduite ![]() , définie par
, définie par ![]() , est égale à
, est égale à ![]() .
.
Théorème: répartition des valeurs de ![]()
Lorsque la variable aléatoire ![]() suit la loi normale centrée réduite
suit la loi normale centrée réduite ![]() , alors pour tout nombre
, alors pour tout nombre ![]() de l’intervalle
de l’intervalle ![]() , il existe un unique nombre réel positif
, il existe un unique nombre réel positif ![]() tel que
tel que
![]()
Valeurs particulières
![]() On a
On a ![]() d’où :
d’où : ![]() .
.
![]() On a
On a ![]() et
et ![]() .
.
3. Loi normale 
Définition
Une variable aléatoire ![]() suit une loi normale
suit une loi normale ![]() si la variable aléatoire
si la variable aléatoire ![]() suit la loi normale centrée réduite
suit la loi normale centrée réduite ![]() .
.
Propriétés: espérance et écart-type de la loi normale ![]()
On admet que, si une variable aléatoire ![]() suit la loi normale
suit la loi normale ![]() }, alors son espérance est égale à
}, alors son espérance est égale à ![]() et son écart-type à
et son écart-type à ![]() :
:
![]()
![]()
Propriétés: intervalles un, deux et trois sigmas
![]()
(à ![]() près)
près)
![]()
(à ![]() près)
près)
![]()
(à ![]() près)
près)
4. Intervalle de fluctuation
En statistiques, un échantillon de taille ![]() est la liste des
est la liste des ![]() résultats obtenus par
résultats obtenus par ![]() répétitions indépendantes de la même expérience aléatoire.
répétitions indépendantes de la même expérience aléatoire.
Par exemple, un échantillon de taille ![]() du lancer d’un dé dont on observe l’apparition ou non de la face
du lancer d’un dé dont on observe l’apparition ou non de la face ![]() est la liste des résultats obtenus en lançant
est la liste des résultats obtenus en lançant ![]() fois le dé. Pour chaque lancer la probabilité de réussir (d’obtenir la face
fois le dé. Pour chaque lancer la probabilité de réussir (d’obtenir la face ![]() ) est
) est ![]() , la probabilité de l’échec (ne pas obtenir
, la probabilité de l’échec (ne pas obtenir ![]() ) est
) est ![]() (
(![]() si le dé est bien équilibré). Le nombre de réussites dans un échantillon de taille
si le dé est bien équilibré). Le nombre de réussites dans un échantillon de taille ![]() suit la loi binomiale
suit la loi binomiale ![]() .
.
On note ![]() la fréquence du nombre de réussites dans l’échantillon.
la fréquence du nombre de réussites dans l’échantillon.
Définition: intervalle de fluctuation à ![]()
Un intervalle de fluctuation au seuil de ![]() , relatif aux échantillons de taille
, relatif aux échantillons de taille ![]() , est un intervalle où se situe la fréquence
, est un intervalle où se situe la fréquence ![]() observée dans un échantillon de taille
observée dans un échantillon de taille ![]() avec une probabilité supérieure à
avec une probabilité supérieure à ![]() .
.
Propriété admise en classe inférieur :
L’intervalle ![]() est un intervalle de fluctuation approché au seuil de
est un intervalle de fluctuation approché au seuil de ![]() , relatif aux échantillons de taille
, relatif aux échantillons de taille ![]() . Dans certains cas, la probabilité que la fréquence appartienne à l’intervalle
. Dans certains cas, la probabilité que la fréquence appartienne à l’intervalle ![]() est très proche de
est très proche de ![]() mais en étant inférieure, c’est pourquoi on dit que ce sont des intervalles de fluctuation « approchés ».
mais en étant inférieure, c’est pourquoi on dit que ce sont des intervalles de fluctuation « approchés ».
Dans la pratique, on utilise l’intervalle ![]() pour des probabilités
pour des probabilités ![]() comprises entre
comprises entre ![]() et
et ![]() et des échantillons de taille
et des échantillons de taille ![]() supérieure à
supérieure à ![]() .
.
Intervalles de fluctuation asymptotique
Dans ce qui suit, on considère des variables aléatoires ![]() suivant chacune une loi binomiale
suivant chacune une loi binomiale ![]() (exemple : on lance
(exemple : on lance ![]() fois une pièce équilibrée,
fois une pièce équilibrée, ![]() est le nombre de « pile » obtenus,
est le nombre de « pile » obtenus, ![]() suit la loi
suit la loi ![]() ).
).
La variable aléatoire ![]() donne donc la fréquence du nombre de « succès ».
donne donc la fréquence du nombre de « succès ».
Propriétés
La variable aléatoire ![]() :
:
![]() prend
prend ![]() valeurs:
valeurs: ![]() .
.
![]() vérifie
vérifie 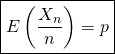 et
et 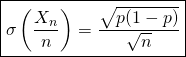
Définition: intervalle de fluctuation asymptotique au seuil ![]()
Un intervalle de fluctuation asymptotique de la variable aléatoire ![]() au seuil
au seuil ![]() est un intervalle déterminé à partir de
est un intervalle déterminé à partir de ![]() et de
et de ![]() et qui contient
et qui contient ![]() avec une probabilité d’autant plus proche de
avec une probabilité d’autant plus proche de ![]() que
que ![]() est grand.
est grand.
Théorème
Soit ![]() un nombre réel fixé de l’intervalle
un nombre réel fixé de l’intervalle ![]() .
.
Soit une suite de variables aléatoires ![]() , chaque variable aléatoire
, chaque variable aléatoire ![]() suivant la loi binomiale
suivant la loi binomiale ![]() .
.
Pour tout réel ![]() dans
dans ![]() , on a:
, on a:
![Rendered by QuickLaTeX.com \[\boxed{\lim\limits_{n \longrightarrow +\infty} P\left(\frac{X_{n}}{n} \in I_{n} \right) = 1 - \alpha}\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-ecf5642effa0e2daef5b4e58ed186524_l3.png)
où
![Rendered by QuickLaTeX.com \[I_{n} = \left[ p - u_{\alpha} \frac{\sqrt{p(1-p)}}{\sqrt{n}} ; p + u_{\alpha} \frac{\sqrt{p(1-p)}}{\sqrt{n}} \right]\]](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-182d06fba0fca6cf8b899939d3c117f0_l3.png)
Remarque. Le nombre ![]() est l’unique réel positif tel que, pour
est l’unique réel positif tel que, pour ![]() une variable aléatoire suivante la loi normale centrée réduite
une variable aléatoire suivante la loi normale centrée réduite ![]() :
:
![]()
Propriété
L’intervalle ![Rendered by QuickLaTeX.com \boxed{I_{n} = \left[ p - u_{\alpha} \frac{\sqrt{p(1-p)}}{\sqrt{n}} ; p + u_{\alpha} \frac{\sqrt{p(1-p)}}{\sqrt{n}} \right]}](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-b5f8bec2d8c83b92bca6546f06d50cad_l3.png) est un intervalle de fluctuation asymptotique
est un intervalle de fluctuation asymptotique
au seuil ![]() de la variable aléatoire
de la variable aléatoire ![]() .
.
Théorème
Soit un réel ![]() de l’intervalle
de l’intervalle ![]() et une suite de variables aléatoires
et une suite de variables aléatoires ![]() où chaque variable aléatoire
où chaque variable aléatoire ![]() suit la loi binomiale
suit la loi binomiale ![]() . Il existe un entier
. Il existe un entier ![]() tel que:
tel que:
![]()
![]()
Intervalle de fluctuation et prise de décision
![]() Si la fréquence observée
Si la fréquence observée ![]() dans un échantillon appartient à un intervalle de fluctuation asymptotique au seuil de
dans un échantillon appartient à un intervalle de fluctuation asymptotique au seuil de ![]() , on considère que l’échantillon est compatible avec le modèle (i.e la loi de probabilité retenue pour décrire l’expérience);=
, on considère que l’échantillon est compatible avec le modèle (i.e la loi de probabilité retenue pour décrire l’expérience);=
![]() Sinon, on considère que l’échantillon n’est pas compatible avec le modèle.
Sinon, on considère que l’échantillon n’est pas compatible avec le modèle.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
5. Estimation
Comme dans la section précédente, on considère une suite de variables aléatoires ![]() où chaque variable aléatoire
où chaque variable aléatoire ![]() suit la loi binomiale
suit la loi binomiale ![]() . La variable
. La variable ![]() donne donc la fréquence du nombre de « succès ».
donne donc la fréquence du nombre de « succès ».
On dit qu’un intervalle est aléatoire lorsque ses bornes sont définies par des
variables aléatoires. La réalisation d’un intervalle aléatoire est l’intervalle obtenu après avoir réalisé l’expérience aléatoire (après avoir lancé 500 fois une pièce, interrogé 1000 personnes…).
Définition: intervalle de confiance
Un intervalle de confiance pour une proportion ![]() à un niveau de confiance de
à un niveau de confiance de ![]() est la réalisation, à partir d’un échantillon, d’un intervalle aléatoire contenant la proportion
est la réalisation, à partir d’un échantillon, d’un intervalle aléatoire contenant la proportion ![]() avec une probabilité supérieure ou égale à
avec une probabilité supérieure ou égale à ![]() .
.
Propriété
Pour une valeur de ![]() fixée, l’intervalle aléatoire
fixée, l’intervalle aléatoire ![]() contient, pour
contient, pour ![]() assez grand, la proportion
assez grand, la proportion ![]() avec une probabilité au moins
avec une probabilité au moins
égale à ![]() .
.
Remarque. On se place dans le cas où l’échantillon contient au moins ![]() éléments. Si la fréquence
éléments. Si la fréquence ![]() observée est telle que
observée est telle que ![]() et
et ![]() , on convient que
, on convient que ![]() est une estimation de
est une estimation de ![]() et que l’intervalle
et que l’intervalle ![]() est
est
un intervalle de confiance au niveau de ![]() pour la proportion
pour la proportion ![]() . Cet intervalle est parfois appelé fourchette de sondage.
. Cet intervalle est parfois appelé fourchette de sondage.
Taille de l’échantillon pour avoir une précision donnée au niveau de confiance de ![]()
La précision de l’estimation est donnée par l’amplitude de l’intervalle ![]() , qui vaut
, qui vaut ![]() et dépend donc de la taille
et dépend donc de la taille ![]() de l’échantillon. On observe cependant que cette amplitude ne dépend pas de la taille de la population
de l’échantillon. On observe cependant que cette amplitude ne dépend pas de la taille de la population
totale, dans laquelle est prélevé l’échantillon.
Si ![]() est la précision souhaitée, on cherche
est la précision souhaitée, on cherche ![]() tel que
tel que ![]() .
.
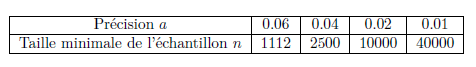
Exercices de probabilités : loi normale, fluctuations et estimation
Exercice 1 :
![]() est une variable aléatoire qui suit la loi normale
est une variable aléatoire qui suit la loi normale ![]() où
où ![]() et
et ![]()
Question 1 :
Montrer que ![]()
Question 2 :
Le réel ![]() tel que
tel que ![]() vérifie
vérifie ![]()
Question 3 :
Montrer que ![]() est strictement inférieure à 0,5
est strictement inférieure à 0,5
Annales sur les probabilités : Loi à densité, loi normale, fluctuations et estimation
Prendre des cours particuliers en maths, est un moyen très efficace pour progresser rapidement et efficacement. Avec un professeur particulier, l’élève aura la possibilité de s’entraîner sur des annales de maths au bac dans les vraies conditions d’examen. Le professeur sera présent également pour donner les bonnes méthodes de travail à l’élève, ce qui lui permettra d’une part, de réussir en terminale, et d’autre part, de réussir facilement lors de ses études supérieures. De plus, avoir une bonne méthodologie de travail peut faire gagner beaucoup de points aux élèves notamment lors des concours aux écoles commerce comme le concours Acces ou le concours Sésame, ainsi que les concours d’écoles d’ingénieurs, le concours Puissance Alpha ou le concours Geipi Polytech par exemple.
Pour les élèves qui préfèrent travailler seuls, les cours en ligne de maths sont de très bons compléments aux cours enseignés pendant les classes au lycée. Les révisions peuvent alors être anticipées et travaillées selon le rythme de l’élève, voici quelques idées de cours à revoir avant le bac :

