Chapitres Maths en Terminale Générale
Cours sur les nombres complexes en terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Suite à la réforme du bac, le programme de maths en terminale a été revu à la hausse, ainsi, le niveau exigé en maths en classe de terminale est plus élevé qu’auparavant. Les élèves qui choisissent l’option maths expertes devront alors, fournir davantage d’efforts. Il est conseillé de prendre des cours particuliers de maths pour exceller durant votre année de terminale en maths. Cependant, cette spécialité permettra de préparer au mieux les élèves aux meilleures prepa scientifiques, comme les meilleures prepa MP ou les meilleures prepa PC.
Résumé de cours : les nombres complexes en Terminale en Maths Expertes
Ce cours en ligne sur les nombres complexes au programme de terminale permet de revoir les notions importantes du cours pour réussir en terminale et obtenir de bons résultats au bac.
1. Calculs dans  en Terminale
en Terminale
1.1. Complexes, partie réelle et imaginaire
![]() On admet l’existence d’un ensemble appelé ensemble des nombres complexes et noté
On admet l’existence d’un ensemble appelé ensemble des nombres complexes et noté ![]() vérifiant les propriétés :
vérifiant les propriétés :
![]()
![]() est un ensemble contenant
est un ensemble contenant ![]() et un élément noté
et un élément noté ![]() tel que
tel que ![]() .
.
![]() Tout élément
Tout élément ![]() s’écrit sous la forme
s’écrit sous la forme ![]() où
où ![]() et
et ![]() sont des réels. Cette écriture, appelée écriture cartésienne de
sont des réels. Cette écriture, appelée écriture cartésienne de ![]() , est unique.
, est unique.
![]() est la partie réelle de
est la partie réelle de ![]() et est notée
et est notée ![]()
![]() est la partie imaginaire de
est la partie imaginaire de ![]() et est notée
et est notée ![]() .
.
![]() Si
Si ![]() où
où ![]() et
et ![]() sont réels,
sont réels, ![]() ssi
ssi ![]() .
.
![]() Si
Si ![]() sont écrits
sont écrits ![]() et
et ![]() où
où ![]() et
et ![]() sont réels,
sont réels,
![]()
![]() .
.
![]() si
si ![]() et si
et si ![]() ,
,
![]()
![]()
![]() .
.
1.2. Conjugué d’un nombre complexe
![]() Si
Si ![]() où
où ![]() et
et ![]() sont réels, le conjugué de
sont réels, le conjugué de ![]() est noté
est noté ![]() et défini par
et défini par ![]() .
.
![]() Propriétés :
Propriétés :
Si ![]() et
et ![]() sont des complexes
sont des complexes
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Si
Si ![]()
![]() Si
Si ![]() ,
,
![]() et
et ![]()
![]() Si
Si ![]()
![]()
![]() est réel ssi
est réel ssi ![]() ssi
ssi ![]()
![]()
![]() est un imaginaire pur ssi
est un imaginaire pur ssi ![]() ssi
ssi ![]() .
.
1.3. Module d’un nombre complexe
![]() Si
Si ![]() est un complexe,
est un complexe, ![]() est un réel positif ou nul.
est un réel positif ou nul.
Le module de ![]() est défini par :
est défini par :
![]()
en écrivant ![]() où
où ![]() et
et ![]() sont réels.
sont réels.
![]() Propriétés :
Propriétés :
Si ![]() et
et ![]() sont des complexes :
sont des complexes :
![]()
![]() .
.
![]() si
si ![]() est un complexe non nul,
est un complexe non nul, ![]() .
.
![]() si
si ![]() est un complexe non nul,
est un complexe non nul,
![]()
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() .
.
1.4. Ensemble des nombres complexes de module 1
On note ![]() l’ensemble des nombres complexes de module 1.
l’ensemble des nombres complexes de module 1.
![]()
![]() ,
, ![]() .
.
![]() Si
Si ![]() ,
,
![]() ,
, ![]() et
et ![]() .
.
![]() Si
Si ![]() et
et ![]() .
.
![]() Si
Si ![]() , pour tout
, pour tout ![]() .
.
![]()
![]() ssi
ssi ![]() .
.
Pour tout complexe ![]() , ,
, , ![]() ,
, ![]() ont même module que
ont même module que ![]() .
.
1.5. Formule du binôme de Newton
Si ![]() et
et ![]() sont des complexes et
sont des complexes et ![]()
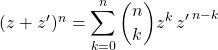
avec ![]()
où ![]()
et si ![]() .
.
Démonstration :
Si ![]() , on note
, on note
![]() :
: 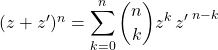
Initialisation : Pour ![]() ,
, 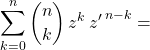
![]()
![]()
On a donc prouvé ![]() .
.
Hérédité : On suppose que ![]() est vraie.
est vraie.
On multiplie l’égalité de ![]() par
par ![]()
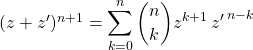
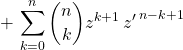
on pose ![]() dans la première somme :
dans la première somme :
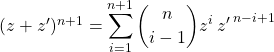
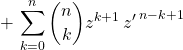
On additionne donc deux expressions :
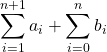
en notant ![]() et
et ![]() .
.
![]() on a un seul indice
on a un seul indice ![]() avec
avec
![]()
![]() car
car ![]() .
.
![]() on a un seul indice
on a un seul indice ![]() , avec
, avec
![]()
![]()
car ![]() .
.
![]() Lorsque
Lorsque ![]()
![]()
![]()
![]()
dont le dénominateur commun est ![]()
![]()
![]()
![]()
et ![]()
ce qui permet d’écrire
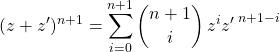
On a prouvé ![]()
Conclusion : la propriété est vraie par récurrence.
1.6. Suite géométrique complexe en maths expertes
![]() Soit
Soit ![]() une suite complexe. C’est une suite géométrique s’il existe
une suite complexe. C’est une suite géométrique s’il existe ![]() (appelé raison)tel que pour tout entier
(appelé raison)tel que pour tout entier ![]() ,
, ![]() .
.
Les propriétés suivantes des suites géométriques réelles sont encore valables :
![]() La suite géométrique
La suite géométrique ![]() de raison
de raison ![]() vérifie
vérifie ![]() pour tout entier
pour tout entier ![]() ,
, ![]()
![]() Soit
Soit ![]() . La suite géométrique
. La suite géométrique ![]() de raison
de raison ![]() vérifie
vérifie ![]() pour tout entier
pour tout entier ![]() ,
, ![]()
![]() Si
Si ![]() et
et ![]() ,
,
![]()
ce qui s’écrit aussi
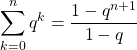 .
.
1.7. Résolution de deux équations d’ordre 1.
![]() Pour résoudre une équation de la forme
Pour résoudre une équation de la forme ![]() dans
dans ![]() , lorsque
, lorsque ![]() , il suffit d’écrire :
, il suffit d’écrire :
![]() .
.
Il vaut mieux éviter d’introduire la partie réelle et imaginaire de ![]() , ce qui alourdit la démonstration
, ce qui alourdit la démonstration
![]() Pour résoudre une équation de la forme
Pour résoudre une équation de la forme ![]() dans
dans ![]() ,
,
Il faut dans ce cas introduire ![]() où
où ![]() et
et ![]() sont réels, et en égalant les parties réelles et imaginaires, on obtient un système de deux équations à deux inconnues.
sont réels, et en égalant les parties réelles et imaginaires, on obtient un système de deux équations à deux inconnues.
2. Plan complexe sur les nombres complexes en terminale
Dans toute la suite, on suppose le plan rapporté à un repère orthonormal direct ![]() .
.
On dit que l’on se place dans le plan complexe.
2.1. Affixe d’un point
![]() À tout complexe
À tout complexe ![]() , on associe le point
, on associe le point ![]() .
.
On dit que ![]() est l’affixe du point
est l’affixe du point ![]() et que
et que ![]() est l’image du complexe
est l’image du complexe ![]() .
.
![]() À tout point
À tout point ![]() de coordonnées
de coordonnées ![]() on associe le complexe
on associe le complexe ![]() .
.
![]() Cas particuliers
Cas particuliers
![]() Un point
Un point ![]() a une affixe réelle ssi il appartient à l’axe des abscisses appelé axe des réels.
a une affixe réelle ssi il appartient à l’axe des abscisses appelé axe des réels.
![]() Un point
Un point ![]() a une affixe imaginaire pure ssi il appartient à l’axe des ordonnées appelé axe des imaginaires purs.
a une affixe imaginaire pure ssi il appartient à l’axe des ordonnées appelé axe des imaginaires purs.
![]() Deux points sont égaux ssi ils ont même affixe.
Deux points sont égaux ssi ils ont même affixe.
![]() Propriétés :
Propriétés :
![]() les images
les images ![]() et
et ![]() de
de ![]() et
et ![]() sont symétriques par rapport à
sont symétriques par rapport à ![]() .
.
![]() Les images
Les images ![]() et
et ![]() de
de ![]() et de
et de ![]() sont symétriques par rapport à l’axe des réels.
sont symétriques par rapport à l’axe des réels.
![]() Les images
Les images ![]() et
et ![]() de
de ![]() et
et ![]() sont symétriques par rapport à l’axe des ordonnées.
sont symétriques par rapport à l’axe des ordonnées.
![]() si
si ![]() est l’image du complexe
est l’image du complexe ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() ont pour affixes
ont pour affixes ![]() et
et ![]() , le milieu
, le milieu ![]() du segment
du segment ![]() a pour affixe
a pour affixe ![]() .
.
2.2. Affixe d’un vecteur
![]() A tout complexe
A tout complexe ![]() , on associe le vecteur
, on associe le vecteur ![]() de coordonnées
de coordonnées ![]() , on dit que
, on dit que ![]() est l’affixe du vecteur
est l’affixe du vecteur ![]()
![]() Réciproquement, à tout vecteur
Réciproquement, à tout vecteur ![]() de coordonnées
de coordonnées ![]() , on associe le complexe
, on associe le complexe ![]() .
.
![]()
![]() est l’affixe du point
est l’affixe du point ![]() ssi
ssi ![]() est l’affixe du vecteur
est l’affixe du vecteur ![]() .
.
![]() Si
Si ![]() est l’affixe de
est l’affixe de ![]() et
et ![]() est l’affixe de
est l’affixe de ![]() ,
, ![]() est l’affixe du vecteur
est l’affixe du vecteur ![]() .
.
![]() Si
Si ![]() est l’affixe de
est l’affixe de ![]() et
et ![]() est l’affixe de
est l’affixe de ![]() ,
, ![]() est l’affixe du point
est l’affixe du point ![]() tel que
tel que ![]() .
.
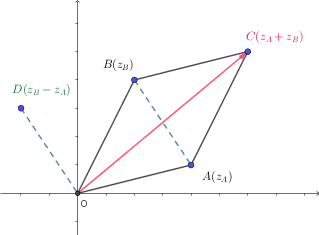
![]() est une diagonale du parallélogramme construit sur
est une diagonale du parallélogramme construit sur ![]() et
et ![]() .
.
![]() est l’affixe du quatrième som- met
est l’affixe du quatrième som- met ![]() du parallélogramme construit sur
du parallélogramme construit sur ![]() et
et ![]() .
.
(voir le dessin ci-dessous)
3. Forme trigonométrique d’un complexe non nul
Dans toute la suite, on suppose le plan rapporté à un repère orthonormal direct ![]() .
.
3.1. Définition de l’argument d’un complexe non nul
![]() Soit
Soit ![]() un complexe non nul.
un complexe non nul.
Il existe un réel ![]() tel que
tel que
![]() et
et ![]() .
.
Et si ![]() est solution, toute autre solution est de la forme
est solution, toute autre solution est de la forme ![]() où
où ![]() .
.
On dit que ![]() est un argument du complexe
est un argument du complexe ![]() et on écrit
et on écrit
![]()
et on lit que l’argument de ![]() est égal à
est égal à ![]() modulo
modulo ![]() .
.
![]() n’a pas d’argument !
n’a pas d’argument !
3.2. Interprétation de l’argument d’un complexe non nul
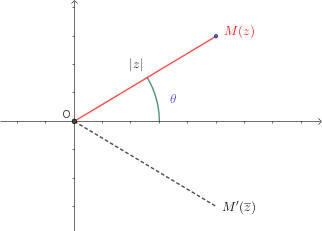
![]() Soit
Soit ![]() un complexe non nul et
un complexe non nul et ![]() son image.
son image.
![]()
![]() est une mesure en radian de l’angle orienté entre
est une mesure en radian de l’angle orienté entre ![]() et
et ![]() ,
,
on note ![]() .
.
![]() Si
Si ![]() est le vecteur image du complexe
est le vecteur image du complexe ![]() ,
, ![]() est une mesure de l’angle de vecteurs
est une mesure de l’angle de vecteurs ![]() .
.
3.3. Propriétés de l’argument d’un complexe non nul
![]() propriétés simples à connaître :
propriétés simples à connaître :
![]()
![]() ssi
ssi ![]()
![]()
![]() ssi
ssi ![]()
![]()
![]() ssi
ssi ![]() est un imaginaire pur à partie imaginaire strictement positive.
est un imaginaire pur à partie imaginaire strictement positive.
![]()
![]() ssi
ssi ![]() est un imaginaire pur à partie imaginaire strictement négative.
est un imaginaire pur à partie imaginaire strictement négative.
![]() Si
Si ![]() est un complexe non nul
est un complexe non nul
![]()
![]()
![]()
![]()
![]()
![]()
![]() si
si ![]() et
et ![]() sont deux complexes non nuls
sont deux complexes non nuls
![]()
![]()
![]() si
si ![]() ,
,![]()
![]()
![]()
![]()
![]()
3.4. Forme trigonométrique
Soit ![]() un complexe non nul, on note
un complexe non nul, on note ![]() et
et ![]()
Alors ![]() .
.
Une telle écriture est appelée la forme trigonométrique du complexe ![]() .
.
![]() Propriété
Propriété
Deux complexes ![]() et
et ![]() non nuls vérifient
non nuls vérifient
![]() ssi
ssi ![]()
3.5. Pour trouver la forme trigonométrique d’un complexe (première partie)
![]() M1. Lorsque l’on a obtenu
M1. Lorsque l’on a obtenu ![]() ,
,
ne pas conclure hâtivement:
![]() si
si ![]() = 0,
= 0, ![]() = 0, module nul, pas d’argument,
= 0, module nul, pas d’argument,
![]() si
si ![]() ,
, ![]() et
et ![]()
![]() si
si ![]() ,
,
![]() et
et ![]() .
.
![]() M2. On peut faire le calcul de
M2. On peut faire le calcul de ![]() , puis écrire
, puis écrire
![]() ,
,
alors il reste à trouver un réel ![]() tel que
tel que
![]() , c’est à dire à trouver un réel
, c’est à dire à trouver un réel ![]() tel que
tel que ![]() et
et ![]() .
.
Les cas particuliers

On rappelle en particulier les formules à apprendre par cœur :
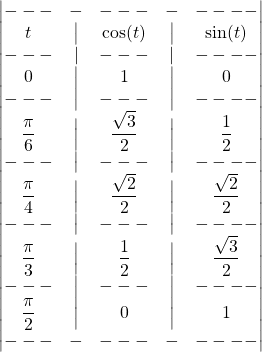
![]() M3. Lorsque
M3. Lorsque ![]() est un produit ou un quotient de deux complexes, il est souvent plus simple de calculer module et argument des deux facteurs du produit ou du quotient et d’appliquer les règles sur les modules et arguments des produits ou des quotients.
est un produit ou un quotient de deux complexes, il est souvent plus simple de calculer module et argument des deux facteurs du produit ou du quotient et d’appliquer les règles sur les modules et arguments des produits ou des quotients.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Formules de trigonométrie programme de maths expertes en terminale
4.1. Formule de trigonométrie pour la fonction cosinus
Pour tous réels ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
Démonstration :
On se place dans le plan complexe muni du repère orthonormé direct ![]()
On note ![]() le cercle de centre
le cercle de centre ![]() et de rayon 1.
et de rayon 1.
On introduit les points ![]() et
et ![]() de
de ![]() tels que
tels que ![]()
et ![]()
alors ![]()
![]()
alors ![]()
![]() .
.
Les coordonnées de ![]() sont
sont ![]() celles de
celles de ![]() sont
sont ![]()
On calcule le produit scalaire :
![]() .
.
On a prouvé que ![]()
et on termine par parité de la fonction ![]() :
:
![]()
Puis en remplaçant ![]() par
par ![]() et comme
et comme ![]() et
et ![]() ,
,
![]()
4.2. Formule de trigonométrie pour la fonction sinus
Pour tous réels ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
Démonstration :
On rappelle que pour tout réel ![]()
![]() ,
, ![]() .
.
![]() .
.
![]() .
.
On utilise la formule donnant ![]() pour
pour ![]()
![]()
![]()
![]() .
.
En remplaçant ![]() par
par ![]() et en utilisant
et en utilisant ![]() et
et ![]()
![]() .
.
4.3. Formule de trigonométrie pour l’angle double
![]() Pour tout réel
Pour tout réel ![]() ,
,
![]()
![]()
![]()
![]()
![]()
Démonstration :
On utilise les formules du début du paragraphe avec ![]()
puis la formule ![]() .
.
5. Fonction exponentielle complexe en maths expertes
5.1. Définition et propriétés de la fonction exponentielle complexe
![]() Si
Si ![]() , on note
, on note
![]() .
.
Cas particuliers
![]()
![]() pour tout
pour tout ![]()
![]()
![]()
![]()
![]() .
.
![]() Propriétés si
Propriétés si ![]() et
et ![]() sont réels
sont réels
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Si
Si ![]() ,
, ![]() .
.
5.2. Formules d’Euler
![]() Pour tout réel
Pour tout réel ![]() ,
,
![]()
![]()
![]() Utilisation pour linéariser (c’est-à-dire transformer un produit en une somme)
Utilisation pour linéariser (c’est-à-dire transformer un produit en une somme)
Pour linéariser une expression de la forme ![]() où
où ![]() et
et ![]() sont dans
sont dans ![]() , remplacer
, remplacer ![]() et
et ![]() par les formules d’Euler, utiliser le binôme de Newton, développer, regrouper les termes en
par les formules d’Euler, utiliser le binôme de Newton, développer, regrouper les termes en ![]() et
et ![]() pour transformer selon le signe en
pour transformer selon le signe en ![]() ou
ou ![]()
![]() Transformer une expression de la forme
Transformer une expression de la forme ![]() ,
, ![]() ou
ou ![]() :
:
remplacer par les formules d’Euler, simplifier et regrouper les termes de la forme ![]() et
et ![]() pour transformer selon le signe en
pour transformer selon le signe en ![]() ou
ou ![]() .
.
5.3. Simplification de fonction exponentielle
![]() M1. Pour simplifier lorsque
M1. Pour simplifier lorsque ![]() et
et ![]() sont réels,
sont réels, ![]() ou
ou ![]() , on met en facteur « e puissance la demi-somme des exposants » ,
, on met en facteur « e puissance la demi-somme des exposants » ,
ce qui donne :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() M2. En particulier, il est conseillé de savoir retrouver très rapidement les formules très utilisées
M2. En particulier, il est conseillé de savoir retrouver très rapidement les formules très utilisées
![]()
![]()
Pour cela, on pose ![]() .
.
5.4. Formule de Moivre
Si ![]() et si
et si ![]()
![]()
![]() .
.
En utilisant le binôme de Newton avec ![]() et
et ![]() ,
,
on développe et en égalant suivant le cas, les parties réelles ou imaginaires, on peut calculer ![]() ou
ou ![]() .
.
5.5. Forme exponentielle d’un complexe non nul
![]() Tout complexe
Tout complexe ![]() non nul peut être écrit sous la forme
non nul peut être écrit sous la forme ![]() où
où
![]() et
et ![]()
![]() est le module de
est le module de ![]()
et ![]()
On a écrit la forme exponentielle du complexe ![]() .
.
Lorsque l’on a obtenu ![]() , ne pas conclure hâtivement:
, ne pas conclure hâtivement:
![]() si
si ![]() = 0,
= 0, ![]() = 0, module nul, pas d’argument,
= 0, module nul, pas d’argument,
![]() si
si ![]() ,
,
![]() et
et ![]() .
.
![]() si
si ![]() ,
,
![]() et
et ![]() .
.
Utilisation pour le module et argument de la somme de deux complexes de même module
Lorsque ![]() , appliquer la transformation indiquée en 5.3. et il faudra faire attention au signe selon de cas de
, appliquer la transformation indiquée en 5.3. et il faudra faire attention au signe selon de cas de ![]() ou de
ou de ![]() (cf ce qui précède)
(cf ce qui précède)
Pour vous préparer au bac, rendez-vous sur les annales de bac en maths, vous pourrez ainsi vous entraîner et tester vos connaissances sur de vrais exercices du bac. Assurez-vous d’obtenir une mention et les notes souhaitées sur le simulateur de bac en prenant des cours particuliers de maths.
N’oubliez pas également d’utiliser les différents cours en ligne de maths au programme de terminale pour vous aider dans vos révisions avant le bac, vérifiez par exemple, votre niveau de connaissances sur les chapitres de maths qui suivent :

