Chapitres Maths en Terminale Générale
Cours variables aléatoires : loi des grands nombres en terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Le niveau de mathématiques au programme de terminale est plus élevé depuis la réforme du bac. La spécialité mathématiques ouvre aux élèves la porte de toutes les classes préparatoire à condition de fournir le travail nécessaire.
Résumé de cours : la loi des grands nombres
Ce cours en ligne sur la loi des grands nombres permet de revoir tous les points essentiels afin de bien réussir et obtenir des bons résultats au bac. Vous pouvez completer ce cours sur la loi des grands nombre avec un prof de maths en ligne.
1. Les variables aléatoires en terminale Maths expertes
1.1. Rappels sur les variables aléatoires en terminale
![]() Toute application
Toute application ![]() est une variable aléatoire réelle sur
est une variable aléatoire réelle sur ![]() . On écrit en abrégé
. On écrit en abrégé ![]() est une v.a.r. sur
est une v.a.r. sur ![]() .
.
![]() Si
Si ![]() est une variable aléatoire sur
est une variable aléatoire sur ![]() ,
, ![]() est une partie finie de
est une partie finie de ![]() , que l’on note
, que l’on note ![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]() L’ensemble des événements
L’ensemble des événements ![]()
est formé de parties non vides, 2 à 2 disjointes, de réunion égale à ![]() (c’est un système complet d’événements).
(c’est un système complet d’événements).
![]() Donner la loi de la variable aléatoire
Donner la loi de la variable aléatoire ![]() c’est donner
c’est donner ![]() et pour tout
et pour tout ![]() , la valeur du réel
, la valeur du réel ![]() .
.
alors : ![]() .
.
![]() Soit
Soit ![]() . Une variable aléatoire
. Une variable aléatoire ![]() suit une loi de Bernoulli de paramètre
suit une loi de Bernoulli de paramètre ![]() si
si ![]() et
et ![]() .
.
Lorsque ![]() est petit, on peut présenter la loi de
est petit, on peut présenter la loi de ![]() sous forme d’un tableau comme celui-ci :
sous forme d’un tableau comme celui-ci :

![]() On peut définir une probabilité
On peut définir une probabilité ![]() sur l’univers fini
sur l’univers fini ![]() par:
par:
pour tout ![]() ,
,
![]()
![]() .
.
On note ![]()
alors ![]() .
.
En particulier
si ![]() ,
, ![]()
si ![]() ,
, ![]()
si ![]() ,
, ![]()
si ![]() ,
, ![]()
si ![]() ,
, ![]()
etc …
1.2. Opérations sur les variables aléatoires en maths expertes
![]() Si
Si ![]() et
et ![]() sont deux variables aléatoires sur l’univers fini
sont deux variables aléatoires sur l’univers fini ![]() , on définit
, on définit
![]() la somme des variables aléatoires
la somme des variables aléatoires ![]() et
et ![]() par
par
![]()
![]() le produit des variables aléatoires
le produit des variables aléatoires ![]() et
et ![]() par
par
![]() .
.
![]() et
et ![]() sont des variables aléatoires sur
sont des variables aléatoires sur ![]() .
.
![]() Si
Si ![]() est une variable aléatoire sur l’univers fini
est une variable aléatoire sur l’univers fini ![]() ,
,
![]() si
si ![]() , on définit le produit de
, on définit le produit de ![]() par le réel
par le réel ![]() par
par
![]()
![]() si
si ![]() ,
,
![]()
![]() et
et ![]() sont des variables aléatoires.
sont des variables aléatoires.
Autres exemples :
Si ![]() ,
, ![]() et si
et si ![]() ,
, ![]() sont des variables aléatoires sur
sont des variables aléatoires sur ![]() ,
,
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
sont des variables aléatoires sur ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
1.3. Indépendance de variables aléatoires
![]() Les variables
Les variables ![]() et
et ![]() définies sur l’univers fini
définies sur l’univers fini ![]() muni de la probabilité
muni de la probabilité ![]() sont dites indépendantes lorsque
sont dites indépendantes lorsque
pour tout ![]() et
et ![]() ,
, ![]()
![]()
c.a.d. les événements ![]() et
et ![]() sont indépendants.
sont indépendants.
![]() Si
Si ![]() et
et ![]() sont des variables indépen- dantes, alors pour tout
sont des variables indépen- dantes, alors pour tout ![]() et
et ![]() ,
,
![]() les événements
les événements ![]() et
et ![]()
![]() les événements
les événements ![]() et
et ![]()
![]() les événements
les événements ![]() et
et ![]()
(etc …) sont indépendants.
Vous n’aurez pas à prouver que les variables aléatoires sont indépendantes, mais si elles sont indépendantes, vous pouvez utiliser l’indépendance des événements ![]() et
et ![]() .
.
Si l’on a ![]() épreuves indépendantes sur l’univers fini
épreuves indépendantes sur l’univers fini ![]() et si pour tout
et si pour tout ![]() ,
, ![]() est une variable aléatoire associée à la
est une variable aléatoire associée à la ![]() -ème épreuve, les
-ème épreuve, les ![]() variables
variables ![]() sont indépendantes et elles sont alors 2 à 2 indépendantes.
sont indépendantes et elles sont alors 2 à 2 indépendantes.
1.4. Espérance d’une variable aléatoire en terminale générale
Soit ![]() une variable aléatoire sur l’univers fini
une variable aléatoire sur l’univers fini ![]() , lorsque
, lorsque ![]()
l’espérance de ![]() est le réel noté
est le réel noté ![]() égal à
égal à 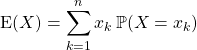 .
.
Interprétation : On suppose que ![]() .
.
On dit que ![]() suit une loi uniforme si
suit une loi uniforme si
pour tout ![]() ,
, ![]()
alors ![]() est la moyenne des valeurs prises par
est la moyenne des valeurs prises par ![]() .
.
![]() Soient
Soient ![]() et
et ![]() deux variables aléatoi- res sur
deux variables aléatoi- res sur ![]() , alors
, alors
![]() .
.
![]() Soit
Soit ![]() une variable aléatoire et
une variable aléatoire et ![]() , alors
, alors
![]() .
.
On traduit ![]() et
et ![]() en disant que l’espérance est linéaire.
en disant que l’espérance est linéaire.
![]() Soit
Soit ![]() une variable aléatoire et
une variable aléatoire et ![]() , alors
, alors
![]()
![]() Soit
Soit ![]() . Si pour tout
. Si pour tout ![]() ,
, ![]() est une variable aléatoire sur l’univers fini
est une variable aléatoire sur l’univers fini ![]()
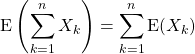 .
.
1.5. La variance en maths expertes en terminale
![]() Si
Si ![]() est une variable aléatoire sur
est une variable aléatoire sur ![]() et si
et si ![]() ,
,
![]() la variance de
la variance de ![]() est le réel positif ou nul :
est le réel positif ou nul :
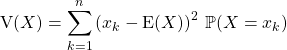
![]() l’écart-type de
l’écart-type de ![]() est le réel positif ou nul noté
est le réel positif ou nul noté ![]() .
.
![]() est l’espérance de la variable aléatoire
est l’espérance de la variable aléatoire ![]() .
.
On peut donc écrire : ![]() .
.
![]() est une mesure de la dispersion de
est une mesure de la dispersion de ![]() autour de
autour de ![]()
![]() Formule de Koenig-Huyghens
Formule de Koenig-Huyghens
![]() .
.
Il est préférable d’utiliser cette formule pour le calcul de ![]() .
.
Si les variables ![]() et
et ![]() ont même loi,
ont même loi, ![]() et
et ![]() .
.
Lorsque ![]() est faible, on peut calculer
est faible, on peut calculer ![]() et
et ![]() en utilisant un tableau du type suivant :
en utilisant un tableau du type suivant :

![]() Propriétés
Propriétés
![]() Si
Si ![]() est une variable aléatoire et
est une variable aléatoire et ![]() un réel,
un réel, ![]() .
.
![]() Si
Si ![]() et
et ![]() sont des variables indépendantes sur
sont des variables indépendantes sur ![]() ,
, ![]() .
.
![]() Soient
Soient ![]() et
et ![]() épreuves indépen- dantes. Si pour tout
épreuves indépen- dantes. Si pour tout ![]() ,
, ![]() est une variable aléatoire associée à la
est une variable aléatoire associée à la ![]() -ème épreuve et si
-ème épreuve et si 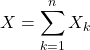 ,
,
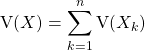 .
.
2. Inégalité de Bienaymé-Tchebychev en maths en Terminale
Inégalité de Bienaymé-Tchebychev
Soit ![]() une variable aléatoire sur
une variable aléatoire sur ![]()
Pour tout ![]() ,
, ![]() .
.
On note ![]() et
et ![]()
On note ![]() l’ensemble des
l’ensemble des ![]() tels que
tels que ![]() et
et ![]() .
.
![]()
On écrit ![]() .
.
En utilisant la partition ![]() de
de ![]()
![]()
![]()
comme on additionne des nombres positifs ou nuls,
![]()
puis si ![]() ,
, ![]()
donc ![]()
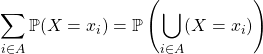 .
.
avec ![]()
ce qui donne ![]()
On obtient le résultat en divisant par ![]() .
.
L’inégalité de Bienaymé-Tchebychev donne donc une majoration de la probabilité pour que ![]() ou que
ou que ![]()
En particulier si ![]() est l’écart type de
est l’écart type de ![]() ,
, ![]() .
.
En prenant ![]() , on obtient une inégalité qui n’a pas d’intérêt car elle s’écrit
, on obtient une inégalité qui n’a pas d’intérêt car elle s’écrit ![]()
On peut aussi écrire l’inégalité de Bienaymé-Tchebychev sous la forme :
pour tout ![]() ,
, ![]() .
.
3. Loi des grands nombres en Terminale
3.1. Échantillon de taille  d’une loi
d’une loi
![]() Soit
Soit ![]() une variable aléatoire définie sur l’univers fini
une variable aléatoire définie sur l’univers fini ![]() .
.
![]() Si
Si ![]() , on appelle échantillon de taille
, on appelle échantillon de taille ![]() de la loi de
de la loi de ![]() toute famille
toute famille ![]() de variables aléatoires indépendantes de même loi que
de variables aléatoires indépendantes de même loi que ![]()
(on les obtient en répétant ![]() épreuves identiques)
épreuves identiques)
![]() On définit
On définit
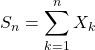 et
et ![]() .
.
![]() est appelée moyenne empirique des variables
est appelée moyenne empirique des variables ![]()
![]() Propriétés
Propriétés
Soient ![]() et
et ![]() de variables aléatoires indépendantes de même loi.
de variables aléatoires indépendantes de même loi.
On note ![]() et
et ![]() l’écart type de
l’écart type de ![]()
![]() et
et ![]()
![]() et
et ![]() .
.
3.2. Inégalité de concentration en maths expertes
Soient ![]() et
et ![]() des variables aléatoires indépendantes de même loi d’espérance
des variables aléatoires indépendantes de même loi d’espérance ![]() et d’écart- type
et d’écart- type ![]() .
.
Alors pour tout ![]() ,
,
![]()
C’est simplement une application de l’inégalité de Bienaymé-Tchebychev, on peut donc la retrouver facilement.
Plus la taille de l’échantillon est importante, plus les valeurs prises par les moyennes empiriques sont regroupées autour de l’espérance de la loi.
3.3. Loi des grands nombres en terminale
Soit une épreuve ![]() et une variable aléatoire
et une variable aléatoire ![]() associée à cette épreuve dont on note
associée à cette épreuve dont on note ![]() l’espérance et
l’espérance et ![]() l’écart type.
l’écart type.
En répétant ![]() fois de façon indépen- dante cette épreuve, on obtient un échantillon
fois de façon indépen- dante cette épreuve, on obtient un échantillon ![]() de taille
de taille ![]() de la loi de
de la loi de ![]() .
.
Pour tout ![]() ,
, ![]()
alors ![]() .
.
On dit que la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() .
.
Cas particulier
Soit ![]() une variable aléatoire de Bernoulli d’espérance
une variable aléatoire de Bernoulli d’espérance ![]() .
.
Soit ![]() et un échantillon
et un échantillon ![]() de taille
de taille ![]() de la loi de
de la loi de ![]() .
.
Pour tout ![]() ,
, ![]()
alors ![]() .
.
On dit que la suite ![]() converge en probabilité vers
converge en probabilité vers ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
Pour vous préparer au bac, rendez-vous sur les annales de bac en maths, vous pourrez ainsi vous entraîner et tester vos connaissances sur de vrais exercices du bac. Assurez-vous d’obtenir une mention et les notes souhaitées sur le simulateur de bac en prenant des cours particuliers de maths.
N’oubliez pas également d’utiliser les différents cours en ligne de maths au programme de terminale pour vous aider dans vos révisions avant le bac, vérifiez par exemple, votre niveau de connaissances sur les chapitres de maths qui suivent :

