Chapitres Maths en Terminale Générale
Exercices et corrigés : Les algorithmes en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Profitez de ces exercices sur les algorithmes et de leurs corrigés gratuits au programme de mathématiques en Terminale pour prendre de l’avance sur vos révisions. Faites un bilan de vos connaissances en algorithmique et commencez votre préparation pour le bac en fin d’année. Utilisez aussi notre simulateur de bac pour déterminer les notes à obtenir à l’examen en fonction des différents coefficients au bac.
On pourra utiliser la notation 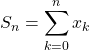 pour représenter la somme
pour représenter la somme ![]() .
.
1. Définir une suite en algorithmique en Terminale
Exercice pour déterminer une suite en algorithmique :
Que donne la fonction suivante lorsque l’on appelle Devine(N) où ![]() est un entier donné ?
est un entier donné ?
def Devine(n):
![]() u = 1
u = 1
![]() for k in range(n):
for k in range(n):
![]() u = (1 + 1/(k + 1)) * u
u = (1 + 1/(k + 1)) * u
![]() return u
return u
Correction de l’exercice pour déterminer une suite en algorithmique :
On calcule ![]()
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2.Termes successifs d’une suite en algorithmique en Terminale Générale
Exercice sur les termes successifs d’une suite en Terminale
On définit la suite ![]() par
par ![]() et pour tout entier
et pour tout entier ![]() ,
, ![]()
Compléter l’algorithme suivant pour que l’appel à Suite ![]() pour un entier
pour un entier ![]() donné fournisse la liste
donné fournisse la liste ![]()
def SuiteU (n):%
![]() u = …
u = …
![]() L =[…]
L =[…]
![]()
![]() for i in range (… ) :
for i in range (… ) :
![]() u = …
u = …
![]() L. append(…)
L. append(…)
![]() return …
return …
Correction de l’exercice sur les termes successifs d’une suite en Terminale
l est indispensable d’initialiser ![]() à
à ![]() .
.
et on initialise la liste avec ![]() car on calcule dans la boucle les termes successifs.
car on calcule dans la boucle les termes successifs.
Dans la boucle, on calcule les ![]() termes suivants de la suite et on les place dans la liste grâce à append.
termes suivants de la suite et on les place dans la liste grâce à append.
Il faut donc faire ![]() calculs donc
calculs donc ![]() décrit range(0 , n)
décrit range(0 , n)
def SuiteU (n):
![]() u = 1/2
u = 1/2
![]() L = [u]
L = [u]
![]()
![]() for i in range (n) :
for i in range (n) :
![]() u = 2 * u / (1 + u)
u = 2 * u / (1 + u)
![]() L. append(u)
L. append(u)
![]() return L
return L
3. Somme des termes d’une suite en algorithmique en Terminale
On définit une suite ![]() par son premier terme
par son premier terme ![]() et la relation
et la relation ![]()
On note 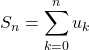 .
.
Exercice sur la sommes des termes d’une suite en Terminale :
Compléter la fonction suivante dont le résultat est ![]() lorsque
lorsque ![]()
def Somme (![]() , n):
, n):
![]() U =
U = ![]()
![]() S =
S = ![]()
![]() for i in range (… ):
for i in range (… ):
![]() S = …
S = …
![]() U = …
U = …
![]() return …
return …
Correction de l’exercice sur la sommes des termes d’une suite en Terminale :
Il est indispensable d’initialiser ![]() avec
avec ![]() pour commencer
pour commencer
Dans la boucle, on met à jour ![]() avant de calculer le terme suivant
avant de calculer le terme suivant
Donc il faut à l’ancienne valeur de ![]() ajouter la valeur de
ajouter la valeur de ![]() calculée auparavant
calculée auparavant
lorsque ![]() ,
, ![]() est égal à
est égal à ![]() et il faut dobc que l’initialisation avant la boucle soit
et il faut dobc que l’initialisation avant la boucle soit ![]()
Dans la boucle sur ![]() , on introduit le nouveau terme pour
, on introduit le nouveau terme pour ![]() .
.
Il faut additionner en tout ![]() éléments donc i doit varier de 0 à
éléments donc i doit varier de 0 à ![]() soit
soit ![]() in range(n + 1).
in range(n + 1).
La réponse attendue est :
def Somme (![]() , n):
, n):
![]() U =
U = ![]()
![]() S = 0
S = 0
![]() for i in range (n + 1):
for i in range (n + 1):
![]() S = S + U
S = S + U
![]() U = 0.8*U + 50
U = 0.8*U + 50
![]() return S
return S
4. Problèmes de seuils en algorithmique
Exercice sur les problèmes de seuils en Terminale
On considère la suite définie par ![]() et
et ![]()
Question 1 :
Écrire une fonction ListedesU de paramètre l’entier ![]() dont le résultat est la liste
dont le résultat est la liste ![]() . N’hésitez pas à revoir le cours sur les limites en terminale pour cette question.
. N’hésitez pas à revoir le cours sur les limites en terminale pour cette question.
Question 2 :
On admet que si ![]() , la suite
, la suite ![]() converge vers 3.
converge vers 3.
Compléter la fonction suivante qui donne le premier entier ![]() tel que
tel que ![]() lorsque
lorsque ![]() est un réel de
est un réel de ![]() .
.
def Proche(e):
![]() N
N![]() …
…
![]() U
U![]()
![]() while abs(U
while abs(U![]() 3)
3) ![]() :
:
![]() N
N ![]()
![]() U
U ![]()
![]() return …
return …
Question 3 :
On admet que la suite ![]() converge vers 3.
converge vers 3.
Montrer que la suite de terme général 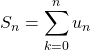 diverge vers
diverge vers ![]() .
.
Ecrire une fonction Depasse (![]() ) dont le résultat est le plus petit entier
) dont le résultat est le plus petit entier ![]() tel que
tel que ![]()
Correction de l’exercice sur les problèmes de seuils en Terminale
Question 1 :
ef ListeDesU(n):
![]() u = 2.5
u = 2.5
![]() L = [u]
L = [u]
![]()
![]() for i in range (n ) :
for i in range (n ) :
![]() u = – u **2 + 5 * u – 3
u = – u **2 + 5 * u – 3
![]() L. append(u)
L. append(u)
![]() return L
return L
ListeDesU(6)
[2.5,3.25,
2.6875,
3.21484375,
2.7389984130859375,
3.1928797585424036,
2.7699176402022196]
Question 2 :
On initialise ![]() ,
, ![]() a été initialisé par l’ énoncé.
a été initialisé par l’ énoncé.
On doit arrêter le while lorsque ![]() donc tant que
donc tant que ![]() , on effectue les instructions de la boucle
, on effectue les instructions de la boucle
![]() on incrémente le compteur N par
on incrémente le compteur N par ![]()
![]() on calcule la valeur suivante de la suite par
on calcule la valeur suivante de la suite par ![]()
Le résultat de la fonction est la dernière valeur de ![]() calculée qui mène à
calculée qui mène à ![]() .
.
def Proche(e):
![]() N
N![]() 0
0
![]() U
U![]()
![]() while abs(U
while abs(U![]() 3)
3)![]() e:
e:
![]() N
N![]() N
N![]()
![]() U=
U= ![]() U**
U**![]() *U
*U![]()
![]() return N
return N
exemples :
Proche(1/100) renvoie 4937
Proche(1/1000) renvoie 499481
Question 3 :
![]() Comme
Comme ![]() , il existe
, il existe ![]() si
si ![]() ,
, ![]() .
.
Si ![]() ,
, 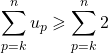
donc ![]()
soit ![]() .
.
Comme ![]()
donc ![]()
![]() Python
Python
def Depasse(A):
![]() U = 2.5
U = 2.5
![]() S = U
S = U
![]() N = 0
N = 0
![]() while S < A:
while S < A:
![]() N = N + 1
N = N + 1
![]() U=
U= ![]() U**
U**![]() *U
*U![]()
![]() S = S + U
S = S + U
![]() return N
return N
Depasse(10000) renvoie 3333.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Suite de Syracuse en Terminale en Algorithmique
Exercice sur les suites de Syracuse en Algorithmique
La suite de Syracuse définie par la donnée d’un terme ![]() et les conditions
et les conditions
pour tout ![]() :
:
![]() si
si ![]() est impair,
est impair, ![]()
![]() si
si ![]() est pair,
est pair, ![]() .
.
On conjecture (la démonstration n’a pas été faite) que quelque soit l’entier >1 de départ, la suite prend la valeur 1.
Ecrire une fonction de paramètre la valeur de départ et qui indique l’indice du premier terme pour lequel on obtient ![]() et donne la liste des valeurs obtenue.
et donne la liste des valeurs obtenue.
Le quotient d’un entier ![]() par 2 est donné par a \\2
par 2 est donné par a \\2
Correction de l’exercice sur les suites de Syracuse en Algorithmique
def Syracuse ( debut ):
![]() u = debut
u = debut
![]() L = [u]
L = [u]
![]()
![]() n = 1
n = 1
![]() while u > 1:
while u > 1:
![]() if u != 2 * (u//2) :
if u != 2 * (u//2) :
![]() u= 3 * u + 1
u= 3 * u + 1
![]() else :
else :
![]() u = u//2
u = u//2
![]() L.append (u)
L.append (u)
![]() n = n + 1
n = n + 1
![]() return n , L
return n , L
Syracuse(11)
(14, [11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1])
Syracuse(17)
(13, [17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1])
Pour Syracuse (121) : on calcule 96 termes !
Pour parfaire votre préparation à l’examen et réviser toutes les notions du programme de terminale, entraînez-vous régulièrement sur les annales du bac en maths, mais également grâce au cours en ligne de Maths au programme de Terminale dont :
- les fonctions exponentielles
- les fonctions logarithmes
- les fonctions trigonométriques
- le conditionnement et l’indépendance
- les primitives
Pour les élèves de Terminale qui rencontrent des difficultés en maths, il est fortement recommandé de se faire accompagner en cours particuliers de maths. Les cours particuliers à domicile ou les cours particuliers en ligne permettent aux élèves d’effacer toutes lacunes et d’adopter les bonnes méthodes de travail

