Chapitres Maths en Terminale Générale
Exercices sur les matrices en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Exercice avec des matrices carrées d’ordre 2 en Terminale
Déterminer les réels ![]() et
et ![]() tels que
tels que ![]()
Exercice autour d’une matrice  d’ordre 2
d’ordre 2
On note ![]() et
et ![]() .
.
Question 1 :
Déterminer lorsqu’elles sont définies les matrices ![]() ,
, ![]() ,
, ![]() ,
, ![]() et donner les réponses en fonction de
et donner les réponses en fonction de ![]() ou
ou ![]() .
.
Question 2 :
La matrice ![]() est inversible ou non inversible ?
est inversible ou non inversible ?
Question 3 :
Déterminer l’ensemble des réels ![]() tels que
tels que ![]() lorsque
lorsque ![]()
(![]() est la matrice colonne à deux lignes nulles).
est la matrice colonne à deux lignes nulles).
On en déduit que ![]() est une matrice inversible ou non inversible ?
est une matrice inversible ou non inversible ?
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercices de matrices d’ordre 3 en Terminale
Exercice 1 sur les matrices d’ordre 3 :
Soit 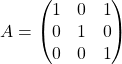
Question 1 :
Calculer ![]() si
si ![]() .
.
Question 2 :
La formule obtenue dans la question 1 est valable pour ![]()
Vrai ou Faux ?
Exercice 2 sur les matrices d’ordre 3 en Terminale Générale
Question 1 :
Avec une calculatrice, calculer l’inverse de 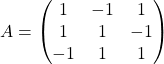
Question 2 :
Résoudre matriciellement le système 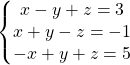
Exercice sur les calculs matriciels en terminale maths expertes
On considère les matrices
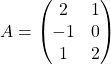 ,
, ![]()
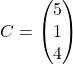 ,
, 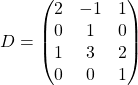
Lorsque c’est possible, calculez les matrices ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Exercice sur les matrices avec de la trigonométrie en terminale
Si ![]() et
et ![]() ,
, ![]() .
.
Vrai ou Faux ?
Exercice pour déterminer une suite en maths expertes
On considère la suite ![]() définie par :
définie par : ![]() et, pour tout entier naturel
et, pour tout entier naturel ![]() ,
, ![]() .
.
On considère de plus les matrices ![]() ,
, ![]() .
.
Question 1 :
Montrer par récurrence que, pour tout entier naturel ![]() , on a :
, on a : ![]() .
.
Question 2 :
Pour tout entier naturel ![]() , on a :
, on a : ![]() .
.
Vrai ou Faux ?
Correction de l’exercice sur des matrices carrées d’ordre 2
![]()
![]()
![]()
On obtient le système 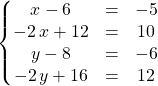
ssi 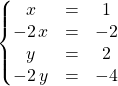
ssi ![]() et
et ![]() .
.
Correction de l’exercice autour d’une matrice  d’ordre 2
d’ordre 2
Question1 :
![]()
![]() est de type
est de type ![]() ,
, ![]() de type
de type ![]() et
et ![]() carrée d’ordre
carrée d’ordre ![]() .
.
On peut définir ![]() et
et ![]() mais on ne peut pas définir
mais on ne peut pas définir ![]() et
et ![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
Question 2 :
On note ![]() la matrice identité d’ordre 2.
la matrice identité d’ordre 2.
La matrice ![]() qui intervient dans la suite est la matrice colonne nulle à deux lignes.
qui intervient dans la suite est la matrice colonne nulle à deux lignes.
On a vu que ![]() , donc
, donc ![]() soit
soit ![]()
ou encore ![]()
Si la matrice ![]() était inversible, en multipliant à gauche la relation
était inversible, en multipliant à gauche la relation ![]() , par la matrice
, par la matrice ![]() , on aurait
, on aurait ![]() soit
soit ![]() soit
soit ![]() donc
donc ![]() , ce qui est impossible.
, ce qui est impossible.
La matrice ![]() n’est pas inversible.
n’est pas inversible.
Question 3 :
![]()
![]() ssi
ssi ![]()
ssi ![]()
ssi ![]()
Les deux équations étant identiques à un facteur multiplicatif près ssi ![]() .
.
![]() En utilisant
En utilisant ![]() ,
, ![]() .
.
Si ![]() était inversible, en multipliant à gauche par
était inversible, en multipliant à gauche par ![]() :
: ![]() donc
donc ![]() ce qui est absurde.
ce qui est absurde.
![]() n’est pas inversible.
n’est pas inversible.
Correction des exercices sur les matrices d’ordre 3
Correction de l’exercice 1 sur les matrices d’ordre 3 :
Question 1 :
On calcule les premières valeurs de ![]() ce qui conduit à poser une conjecture que l’on démontre par récurrence.
ce qui conduit à poser une conjecture que l’on démontre par récurrence.
Si ![]() ,
, ![]() :
: 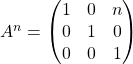 .
.
![]() Initialisation
Initialisation ![]() est évidente.
est évidente.
![]() Hérédité
Hérédité
On suppose que ![]() est vraie
est vraie
![]()
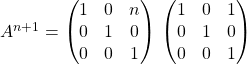
donc 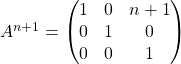
On a prouvé que ![]() est vraie.
est vraie.
![]() Conclusion
Conclusion
La propriété est vraie par récurrence pour tout ![]()
Question 2 :
Vrai,
On introduit ![]() la matrice obtenue en remplaçant
la matrice obtenue en remplaçant ![]() par
par ![]() :
:
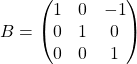 .
.
Un calcul simple donne ![]()
Donc ![]() est inversible et
est inversible et ![]() .
.
La propriété est donc encore vraie pour ![]() .
.
Correction de l’exercice 2 sur les matrices d’ordre 3 en Terminale Générale :
Question 1 :
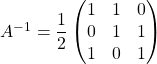 .
.
Question 2 :
On écrit le système sous la forme
![]() où
où 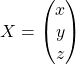 et
et 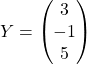
Comme ![]() est inversible d’ordre 3, on peut multiplier la matrice
est inversible d’ordre 3, on peut multiplier la matrice ![]() de type
de type ![]() à gauche par la matrice
à gauche par la matrice ![]() :
:
On obtient ![]() soit
soit ![]() donc
donc ![]() .
.
Dans le cours, on a vu que la réciproque est vraie.
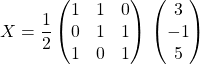
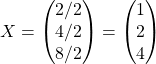
Les solutions sont ![]() ,
, ![]() et
et ![]() .
.
Correction de l’exercice sur les calculs matriciels en maths expertes
Il faut bien sûr avant tout calcul vérifier que le produit est défini.
Je donne uniquement les résultats dans la suite :
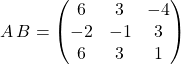
![]()
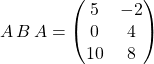
![]()
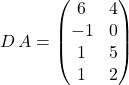
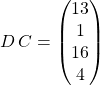
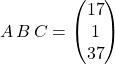
Le produit ![]() n’a pas de sens car
n’a pas de sens car ![]() est de type
est de type ![]() et
et ![]() de type
de type ![]() , donc
, donc ![]() n’a pas de sens.
n’a pas de sens.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur les matrices avec de la trigonométrie
Vrai,
Si ![]() , on note
, on note ![]() :
: ![]()
![]() Initialisation
Initialisation
![]() et
et ![]()
donc ![]() est vraie.
est vraie.
![]() Hérédité
Hérédité
On suppose que ![]() est vraie.
est vraie.
![]() .
.
Par ![]() ,
, ![]()
![]() .
.
On a donc obtenu ![]() .
.
![]() Conclusion
Conclusion
Par récurrence, ![]() est vraie pour tout entier
est vraie pour tout entier ![]() .
.
Correction de l’exercice pour déterminer une suite avec des matrices
Question 1 :
Si ![]() , on note
, on note
![]() ,
, ![]() .
.
![]() Initialisation.
Initialisation.
Si ![]() ,
,
![]()
![]()
![]()
![]() .
.
On a prouvé que ![]() est vraie.
est vraie.
![]() Hérédité.
Hérédité.
On suppose que ![]() est vraie.
est vraie.
On écrit ![]()
![]()
![]()
![]() .
.
On fait quelques calculs intermédiaires :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
donc ![]() .
.
On a prouvé que ![]() est vraie.
est vraie.
![]() Conclusion : la propriété est vraie par récurrence sur
Conclusion : la propriété est vraie par récurrence sur ![]() .
.
On remarque que la propriété est aussi vraie au rang 0 car si ![]() ,
,
![]()
![]() ,
,
donc ![]() est vraie.
est vraie.
Question 2 :
Vrai,
Si ![]() , on note
, on note ![]()
![]() .
.
![]() Initialisation.
Initialisation.
Si ![]() ,
, ![]()
![]() , donc
, donc ![]() est vraie.
est vraie.
![]() Hérédité.
Hérédité.
On suppose que ![]() est vraie.
est vraie.
![]()
![]() .
.
On a prouvé que ![]() est vraie.
est vraie.
![]() Conclusion : la propriété est vraie par récurrence sur
Conclusion : la propriété est vraie par récurrence sur ![]() .
.
Lire son cours de maths n’est pas suffisant pour être certain d’avoir assimilé le cours dans son intégralité. C’est pourquoi les entrainements sur des exercices de cours ou même sur des annales de bac sont recommandés. C’est en appliquant vos connaissances sur des cas concrets que vous pourrez vous rendre compte de vos acquis et de vos difficultés. Après avoir réalisé la série d’exercices ci-dessus, vérifiez vos acquis sur d’autres cours :

