Chapitres Maths en Terminale Générale
Exercices et corrigés : primitives et équations différentielles
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Entraînez-vous avec les exercices et les corrigés sur les calcul de primitive et d’équation différentielle. Cela vous aidera à obtenir une meilleure moyenne en maths et à vous entraîner efficacement pour les épreuves du baccalauréat.
1. Calcul Primitives
Exercice 1 : lecture graphique d’une primitive :
Soit ![]() une fonction dérivable de dérivée continue et
une fonction dérivable de dérivée continue et ![]() une primitive de
une primitive de ![]() sur l’intervalle
sur l’intervalle ![]() .
.
On a représenté les fonctions ![]() ,
, ![]() et
et ![]() dans le même repère.
dans le même repère.
Donner les valeurs ![]() et
et ![]() telles que
telles que ![]() est le graphe de
est le graphe de ![]() ,
, ![]() celui de
celui de ![]() et
et ![]() celui de
celui de ![]() .
.
Exercice 2 : primitive d’une fonction
Déterminer les primitives des fonctions suivantes en précisant l’intervalle de définition.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
2. Calcul Equation différentielle
Exercice 1 Equations différentielles : résoudre une équation
- Résoudre l’équation
 en cherchant une solution particulière sous la forme
en cherchant une solution particulière sous la forme  où
où 
- Résoudre
 en cherchant une solution particulière sous la forme
en cherchant une solution particulière sous la forme  ..
.. - Résoudre l’équation
 en cherchant une solution particulière sous forme d’une fonction polynôme de degré 3.
en cherchant une solution particulière sous forme d’une fonction polynôme de degré 3.
Exercice 2 Equations différentielles : trouver la solution
- Déterminer les solutions de
 sur
sur ![Rendered by QuickLaTeX.com I =\; ]0 , + \infty[](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2091%2018%22%3E%3C/svg%3E) .
.
Indication : On cherchera une fonction ![]() telle que pour tout
telle que pour tout ![]() ,
, ![]() .
.
- Démontrer et déterminer qu’il existe une seule solution
 telle que
telle que  et
et  .
. - Soit
 une fonction deux fois dérivable sur un intervalle
une fonction deux fois dérivable sur un intervalle  . Calculer la dérivée seconde de
. Calculer la dérivée seconde de  .
.
Correction de l’exercice 1 sur les primitives :
On utilise la propriété suivante :
Si le graphe d’une fonction ![]() a une tangente horizontale en
a une tangente horizontale en ![]() , alors
, alors ![]() .
.
On va donc raisonner suivant le nombre de points où les courbes coupent l’axe horizontal.
Toutes les courbes ont des points à tangente horizontale.
![]()
![]() a deux points à tangente horizon- tale et ne coupe pas l’axe
a deux points à tangente horizon- tale et ne coupe pas l’axe ![]() .
.
![]()
![]() a quatre points à tangente horizon- tale et coupe trois fois l’axe
a quatre points à tangente horizon- tale et coupe trois fois l’axe ![]() .
.
![]()
![]() a trois points à tangente horizon- tale et coupe deux fois l’axe
a trois points à tangente horizon- tale et coupe deux fois l’axe ![]() .
.
On note ![]() la fonction de graphe
la fonction de graphe ![]() si
si ![]() .
.
![]() On en déduit que
On en déduit que ![]() n’est pas la dérivée de
n’est pas la dérivée de ![]() ou de
ou de ![]() .
.
Donc ![]() et
et ![]() .
.
![]() Les tangentes à
Les tangentes à ![]() sont horizontales en
sont horizontales en ![]() et
et ![]() .
.
![]() est la courbe qui coupe l’axe
est la courbe qui coupe l’axe ![]() aux points d’abscisse
aux points d’abscisse ![]() et
et ![]() , donc
, donc ![]() a pour courbe représentative
a pour courbe représentative ![]() , alors
, alors ![]() .
.
![]() Et pour vérification :
Et pour vérification :
Les tangentes à ![]() sont horizontales en
sont horizontales en ![]() ,
, ![]() et et
et et ![]() . La courbe
. La courbe ![]() coupe
coupe ![]() aux points d’abscisse
aux points d’abscisse ![]() , donc c’est la courbe représentative de
, donc c’est la courbe représentative de ![]() . Ce qui donne
. Ce qui donne ![]() .
.
Correction de l’exercice 2 sur les primitives :
- On cherche une primitive sur
 ou sur
ou sur  .
.

Les primitives sont les fonctions
 où
où  .
. - On cherche une primitive sur



Les primitives sont les fonctions où
où  .
. - On cherche une primitive sur
![Rendered by QuickLaTeX.com I_1 = \; ]\infty,\, 1[](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2087%2018%22%3E%3C/svg%3E) ou sur
ou sur ![Rendered by QuickLaTeX.com I_ 2 =\; ]1 ,\, + \infty[](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20101%2018%22%3E%3C/svg%3E) .Comme
.Comme 

on peut simplifier l’expression de ,
,


 .
.
Les primitives sur ![]() (puis sur
(puis sur ![]() ) sont les fonctions
) sont les fonctions
![]() où
où ![]()
- On cherche une primitive sur
 .
.
Les primitives sont où
où  .
.
Correction de l’exercice 1 sur les équations différentielles
1. La solution générale de l’équation ![]() est
est ![]() où
où ![]() .
.
Soit ![]()
Pour tout réel ![]() ,
, ![]()
Pour tout réel ![]() ,
, ![]()
ssi ![]() ssi
ssi ![]() .
.
L’ensemble des solutions est l’ensemble des fonctions
![]() où
où ![]() .
.
2. La solution générale de l’équation ![]() est
est ![]() où
où ![]() .Soit pour
.Soit pour ![]() ,
, ![]()
![]()
![]()
![]() .
.
Pour tout réel ![]() ,
,
![]()
ssi pour tout réel ![]() ,
,
![]()
![]()
ssi ![]()
ssi ![]()
ssi ![]() ,
, ![]()
Donc ![]() est une solution pariculière de l’équation.
est une solution pariculière de l’équation.
La solution générale de l’équation ![]() est
est ![]() où
où ![]() .
.
3. ![]() La solution générale de l’équation homogène
La solution générale de l’équation homogène ![]() soit
soit ![]() est
est ![]() où
où ![]() .
.
![]() Soit si
Soit si ![]() ,
, ![]()
![]()
Pour tout réel ![]() ,
,
![]()
ssi pour tout réel ![]()
![]()
![]()
ssi 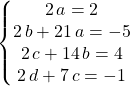
ssi 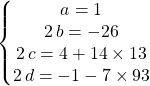
L’ensemble des solutions est l’ensemble des fonctions ![]() où
où ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice 2 sur les équations différentielles
- Comme la fonction
 ne s’annule pas, la fonction
ne s’annule pas, la fonction  est deux fois dérivable ssi la fonction
est deux fois dérivable ssi la fonction  définie par
définie par 
est deux fois dérivable sur .En notant donc pour
.En notant donc pour  ,
, 


et


![]() est solution sur
est solution sur ![]() ssi pour tout
ssi pour tout ![]() ,
,
![]()
![]()
![]()
ssi pour tout ![]() ,
, ![]()
ssi il existe ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]()
ssi il existe deux réels ![]() et
et ![]() tels que pour tout
tels que pour tout ![]() ,
, ![]() .
.
L’ensemble des solutions est l’ensemble des fonctions ![]()
où ![]() et
et ![]() sont réels.
sont réels.
- On cherche
 et
et  tels que
tels que  et
et  .
.
En utilisant
et
on obtient les conditions équivalentes et
et 
ssi
ssi et
et 
ssi et
et 
(on a repris les expressions de et
et  obtenues dans la question précédente).
obtenues dans la question précédente).
Le problème admet une unique solution définie par 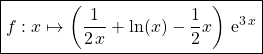 .
.




 .
.
Retrouvez la suite des exercices sur l’application mobile Preapp. Vous y trouverez notamment le reste des exercices des cours en ligne en mathématiques en terminale. Par ailleurs, vous pouvez faire appel à un professeur particulier pour vous aider à mieux comprendre certaines notions. Enfin, vous pouvez d’ores et déjà retrouvez les chapitres suivant sur notre site :

