Chapitres Maths en Terminale Générale
Les fonctions trigonométriques en terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Résumé de cours sur les fonctions trigonométriques en Terminale :
Entraînez-vous et vérifiez vos connaissances grâce à notre cours en ligne sur le chapitre des fonctions trigonométriques au programme de maths en terminale. Certaines notions du chapitre peuvent poser des difficultés, c’est pourquoi de nombreux élèves du lycée et notamment de terminale font appel à un professeur particulier de maths. Prendre des cours particuliers de maths, permet à l’élève de se rassurer et de venir plus confiant en cours et par conséquent plus confiant pour la préparation du bac en fin d’année. Ces cours particuliers peuvent bien entendu être des cours particuliers à domicile comme des cours particuliers en ligne.
Plan du cours sur les fonctions trigonométriques de Terminale
1. Rappels : parité et périodicité
2. En utilisant le cercle trigonométrique
3. Étude de la fonction cosinus
4. Étude de la fonction sinus
5. Équation ![]() et inéquation
et inéquation ![]()
6. Équation ![]() et inéquation
et inéquation ![]()
On suppose dans tout le chapitre que l’on se place dans le plan usuel ![]() rapporté au repère orthonormé direct
rapporté au repère orthonormé direct ![]() .
.
1. Rappels : parité et périodicité des fonctions trigonométriques
![]() Soit
Soit ![]() un vecteur.
un vecteur.
La translation de vecteur ![]() est l’application
est l’application ![]() avec
avec ![]() .
.
Si ![]() , si
, si ![]() a pour coordonnées
a pour coordonnées ![]() ,
, ![]() a pour coordonnées
a pour coordonnées
![]()
![]() et
et ![]() .
.
![]() Soit
Soit ![]() un intervalle de
un intervalle de ![]() centré en
centré en ![]() (c’est-à-dire de la forme
(c’est-à-dire de la forme ![]() ,
, ![]() où
où ![]() ou
ou ![]() ).
).
Soit ![]() .
.
![]()
![]() est une fonction paire si pour tout
est une fonction paire si pour tout ![]() ,
, ![]() .
.
Si ![]() est une fonction paire, son graphe est symétrique par rapport à l’axe
est une fonction paire, son graphe est symétrique par rapport à l’axe ![]() .
.
![]()
![]() est une fonction impaire si pour tout
est une fonction impaire si pour tout ![]() ,
, ![]() .
.
Si ![]() est impaire, son graphe est symétrique par rapport au point
est impaire, son graphe est symétrique par rapport au point ![]() .
.
![]() Soit
Soit ![]() et
et ![]() une partie de
une partie de ![]() telle que si
telle que si ![]() ,
,
![]() pour tout
pour tout ![]() .
.
Soit ![]() .
.
![]() est une fonction périodique de période
est une fonction périodique de période ![]() lorsque pour tout
lorsque pour tout ![]() ,
, ![]() .
.
Pour une fonction périodique de période ![]() et paire ou impaire, choisir de l’étudier
et paire ou impaire, choisir de l’étudier
![]() d’abord sur
d’abord sur ![]() (utilisation de la périodicité)
(utilisation de la périodicité)
![]() puis par la suite sur
puis par la suite sur ![]() (pour utiliser la parité).
(pour utiliser la parité).
2. En utilisant le cercle trigonométrique en Terminale
On note ![]() le cercle de centre
le cercle de centre ![]() et de rayon 1.
et de rayon 1.
Soit ![]() de
de ![]() tel que
tel que ![]() soit une mesure de l’angle
soit une mesure de l’angle ![]() .
.
On rappelle les résultats :
![]() Tout réel
Tout réel ![]() est aussi une mesure de l’angle
est aussi une mesure de l’angle ![]() et que l’on écrit
et que l’on écrit ![]() .
.
![]() Les coordonnées de
Les coordonnées de ![]() sont
sont ![]() .
.
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]() .
.
![]() Pour tout réel
Pour tout réel ![]() ,
,
![]()
![]() et
et ![]()
ce que l’on traduit en disant que les fonctions ![]() et
et ![]() sont périodiques de période
sont périodiques de période ![]() .
.
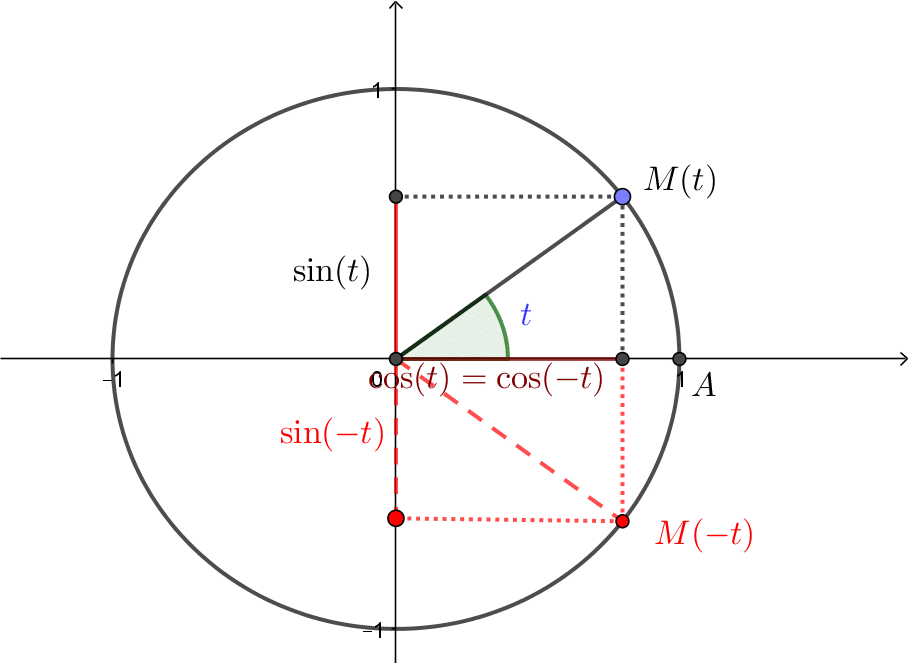
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]() et
et ![]() ,
,
ce que l’on traduit en disant que la fonction ![]() est paire et la fonction
est paire et la fonction ![]() est impaire.
est impaire.
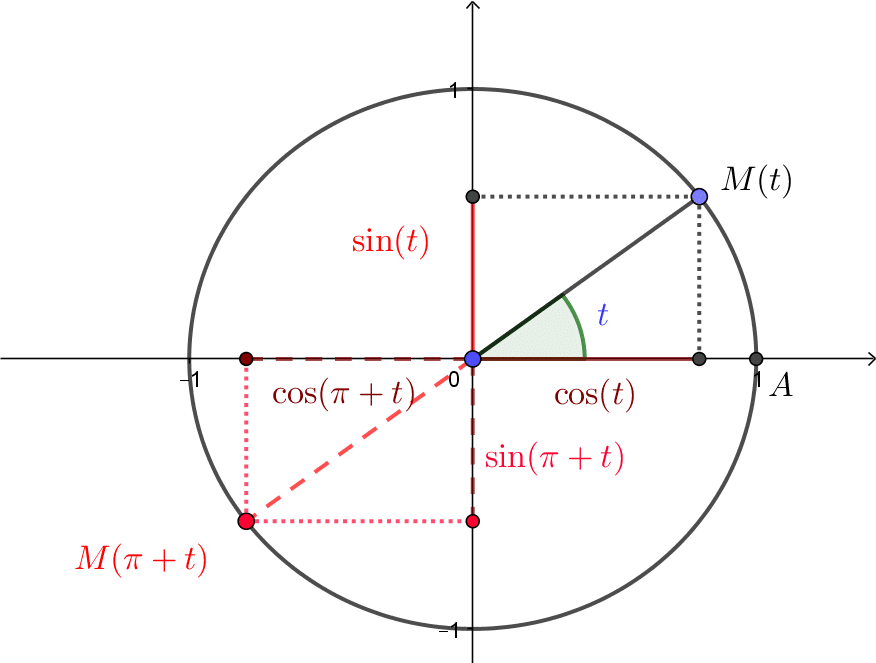
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]()
![]() et
et ![]()
en utilisant ![]() et
et ![]() sont symétriques par rapport à
sont symétriques par rapport à ![]() .
.
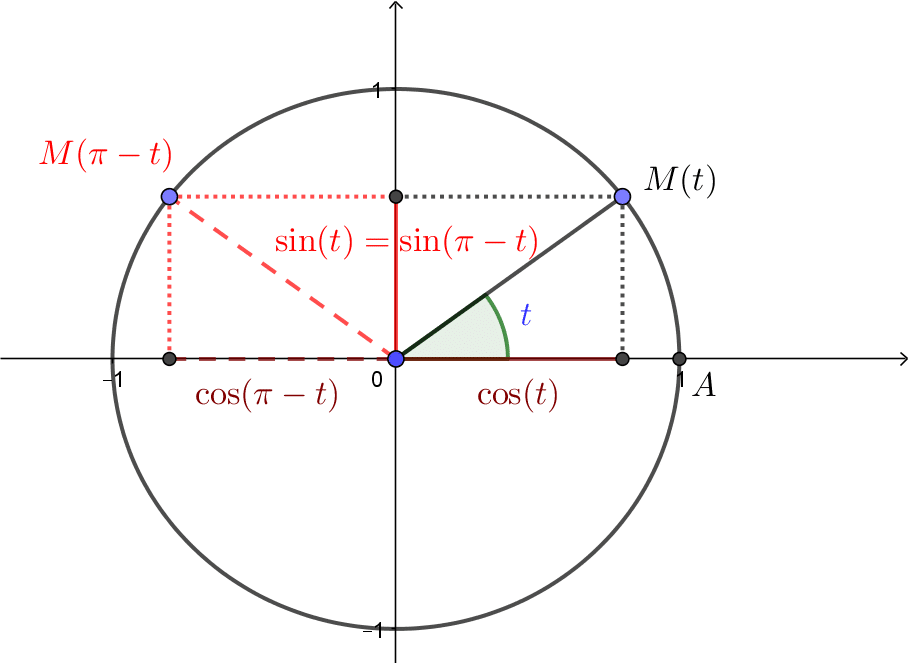
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]()
![]() et
et ![]()
en utilisant ![]() et
et ![]() sont symétriques par rapport à
sont symétriques par rapport à ![]() .
.
![]() Pour tout réel
Pour tout réel ![]() ,
, ![]()
![]() et
et ![]() .
.
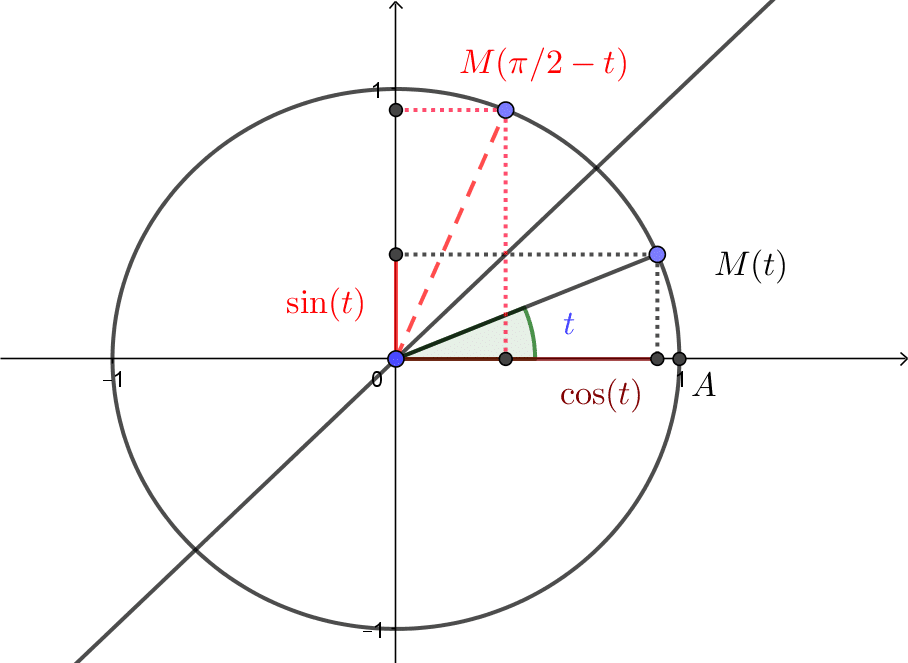
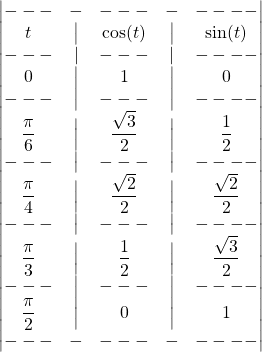
![]() Les valeurs à connaître
Les valeurs à connaître
3. Etude de la fonction cosinus, fonction trigonométrique de Terminale
![]() La fonction cosinus est définie et continue sur
La fonction cosinus est définie et continue sur ![]() , périodique de période
, périodique de période ![]() et paire.
et paire.
Il suffit de l’étudier sur : ![]() et enfin sur
et enfin sur ![]() .
.
On complète le graphe par symétrie par rapport à l’axe ![]() puis par translation de vecteur
puis par translation de vecteur ![]() .
.
![]() La fonction cosinus est dérivable sur
La fonction cosinus est dérivable sur ![]() et de dérivée
et de dérivée ![]()
Elle est strictement décroissante sur ![]() .
.
Remarque Pour tout réel ![]() ,
, ![]() .
.
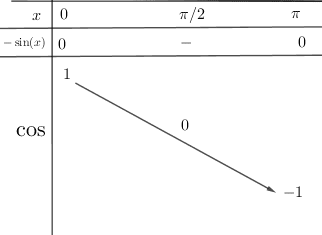
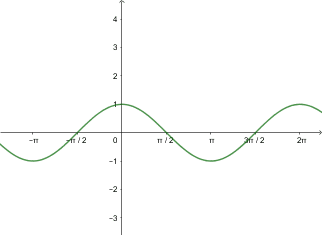
![]() On obtient donc le tableau de variation suivant et le graphe :
On obtient donc le tableau de variation suivant et le graphe :
![]() Si
Si ![]() est une fonction dérivable sur l’intervalle
est une fonction dérivable sur l’intervalle ![]() ,
, ![]() est une fonction dérivable sur
est une fonction dérivable sur ![]() et si
et si ![]() ,
, ![]() .
.
![]() La fonction
La fonction ![]() est continue et strictement décroissante sur
est continue et strictement décroissante sur ![]() avec
avec ![]() et
et ![]() , donc pour tout
, donc pour tout ![]() , il existe un unique
, il existe un unique ![]() tel que
tel que ![]() .
.
![]() La fonction
La fonction ![]() n’a pas de limite en
n’a pas de limite en ![]() .
.
![]()
![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
4. Etude de la fonction sinus, fonction trigonométrique de Terminale
![]() La fonction sinus est définie et continue sur
La fonction sinus est définie et continue sur ![]() , périodique de période
, périodique de période ![]() et impaire.
et impaire.
Il suffit de l’étudier sur ![]() et enfin sur
et enfin sur ![]() .
.
On le complète par symétrie par rapport au point ![]() puis par translation de vecteur
puis par translation de vecteur ![]() .
.
![]() La fonction sinus est dérivable sur
La fonction sinus est dérivable sur ![]() et de dérivée
et de dérivée ![]() .
.
Elle est strictement croissante sur ![]() et strictement décroissante sur
et strictement décroissante sur ![]() .
.
Remarque : Pour tout réel ![]() ,
, ![]() .
.
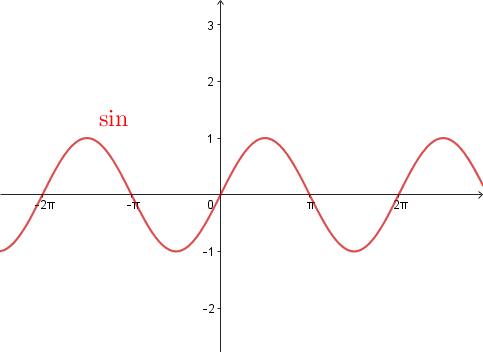
![]() On obtient donc le tableau de variation suivant et le graphe :
On obtient donc le tableau de variation suivant et le graphe :
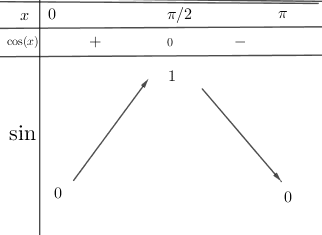
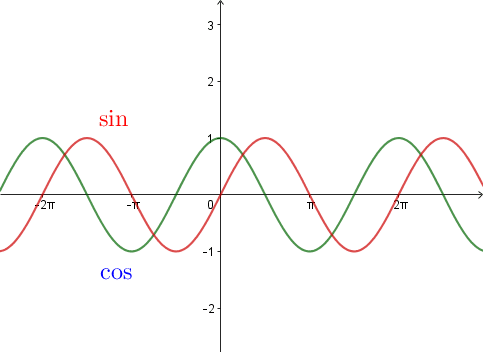
Dans le même repère, les graphes des fonctions ![]() et
et ![]() .
.
![]() Si
Si ![]() est une fonction dérivable sur l’intervalle
est une fonction dérivable sur l’intervalle ![]() ,
, ![]() est une fonction dérivable sur
est une fonction dérivable sur ![]() et si
et si ![]() ,
, ![]() .
.
![]() La fonction
La fonction ![]() n’a pas de limite en
n’a pas de limite en ![]() .
.
![]()
![]()
5. Équation 

L’équation  en Trigonométrie en Terminale
en Trigonométrie en Terminale
![]() Si
Si ![]() , l’équation
, l’équation ![]() n’a pas de solution.
n’a pas de solution.
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]() Si
Si ![]() , on peut trouver
, on peut trouver ![]() tel que
tel que ![]() .
.
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() ou
ou ![]()
L’inéquation ![Rendered by QuickLaTeX.com \cos(x) \leqslant a]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2083%2019%22%3E%3C/svg%3E) en Trigonométrie en Terminale
en Trigonométrie en Terminale
![]() Si
Si ![]() , l’équation
, l’équation ![]() n’a pas de solution.
n’a pas de solution.
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]() Si
Si ![]() , on peut trouver
, on peut trouver ![]() tel que
tel que ![]() .
.
![]() ssi il existe
ssi il existe ![]() tel que
tel que
![]() .
.
![]() Si
Si ![]() , l’ensemble des solutions est
, l’ensemble des solutions est ![]() .
.
Si ![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
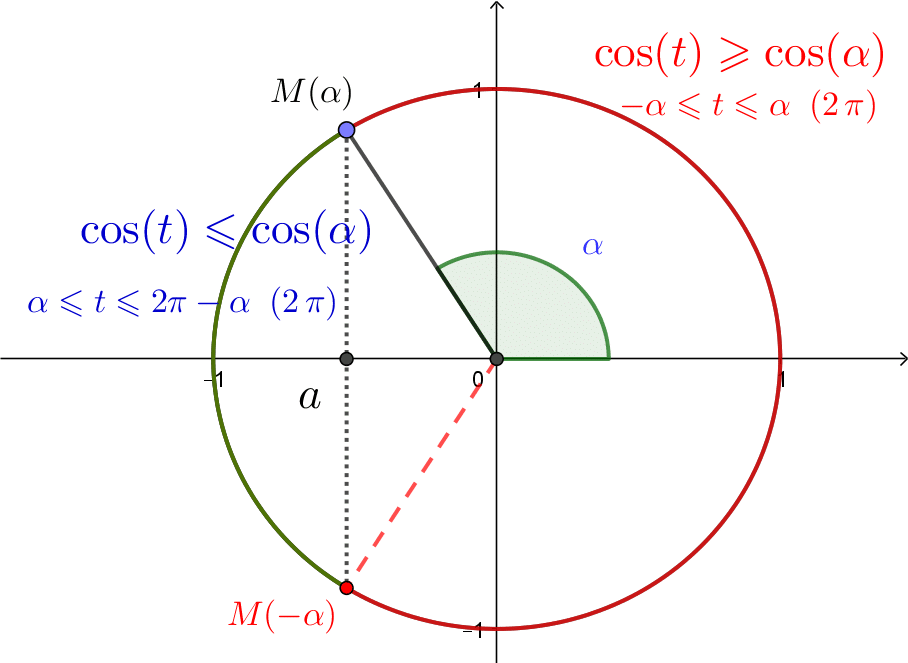
6. Équation 


Équation 
![]() Si
Si ![]() , l’équation
, l’équation ![]() n’a pas de solution.
n’a pas de solution.
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]() Si
Si ![]() , on peut trouver
, on peut trouver ![]() tel que
tel que ![]() .
.
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]()
![]() ou
ou ![]() .
.
Inéquation 
![]() Si
Si ![]() , l’équation
, l’équation ![]() n’a pas de solution.
n’a pas de solution.
![]()
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
![]() Si
Si ![]() , on peut trouver
, on peut trouver ![]() tel que
tel que ![]() .
.
![]() ssi il existe
ssi il existe ![]() tel que
tel que
![]() .
.
![]() Si
Si ![]() , l’ensemble des solutions est
, l’ensemble des solutions est ![]() .
.
Si ![]() ,
,
![]() ssi il existe
ssi il existe ![]() tel que
tel que ![]() .
.
Une bonne préparation au bac est une préparation qui a été faite sur le long terme. Ainsi, si l’élève de terminale s’entraîne régulièrement sur les annales du bac en maths, et sur des cours de mathématiques en ligne en Terminale dont :
- le conditionnement et l’indépendance
- les primitives
- la dérivation et la convexité
- le calcul intégral
- la loi Normale, les intervalles et l’estimation
il n’aura aucun difficulté à réaliser les exercices le jour de examen, obtiendra de très bons résultats au bac et n’aura aucun difficulté à obtenir une mention.

