Chapitres Maths en Terminale Générale
Limites de fonctions en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Révisez votre chapitre de maths sur les limites de fonction au programme de maths en Terminale. La terminale est la dernière ligne droite avant le bac, il est ainsi primordial de préparer cet examen dès les premier jours de cours. Pour maximiser leurs résultats et leurs chances de réussite, les élèves peuvent suivre pendant les vacances, un stage de préparation au bac ou des cours de maths à domicile.
Cours en ligne sur les limites de fonctions en classe de Terminale
1. Connaître la définition d’une limite en 
1.1. Limite d’une fonction en 
Dans ce paragraphe, on suppose que la fonction ![]() est définie sur un ensemble
est définie sur un ensemble ![]() et qu’il existe
et qu’il existe ![]() tel que
tel que ![]() . On note
. On note ![]() son graphe.
son graphe.
![]() Def1 : Soit
Def1 : Soit ![]() , la fonction
, la fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() si elle vérifie l’une des deux conditions équivalentes suivantes :
si elle vérifie l’une des deux conditions équivalentes suivantes :
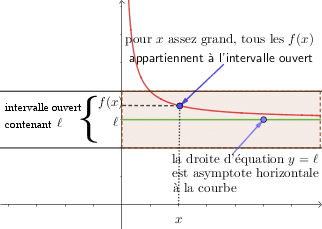
![]() tout intervalle ouvert
tout intervalle ouvert ![]() conte- nant
conte- nant ![]() contient toutes les valeurs
contient toutes les valeurs ![]() pour
pour ![]() assez grand, ce qui veut dire qu’il existe
assez grand, ce qui veut dire qu’il existe ![]() tel que si
tel que si ![]() ,
, ![]()
![]() pour tout
pour tout ![]() , il existe
, il existe ![]() tel que si
tel que si ![]() ,
, ![]() .
.
On écrit alors
![]() ou
ou ![]() .
.
![]() Def2 : La fonction
Def2 : La fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() si elle vérifie l’une des deux conditions équivalentes suivantes
si elle vérifie l’une des deux conditions équivalentes suivantes
![]() pour tout
pour tout ![]() , l’intervalle
, l’intervalle ![]() contient toutes les valeurs
contient toutes les valeurs ![]() pour
pour ![]() assez grand
assez grand
![]() pour tout
pour tout ![]() , il existe
, il existe ![]() tel que si
tel que si ![]() ,
, ![]() .
.
On écrit alors
![]() ou
ou ![]()
![]() Def3 : La fonction
Def3 : La fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() si pour tout
si pour tout ![]() , l’intervalle
, l’intervalle ![]() contient toutes les valeurs
contient toutes les valeurs ![]() pour
pour ![]() assez grand.
assez grand.
On écrit alors
![]() ou
ou ![]()
1.2. Limite d’une fonction en 
Dans ce paragraphe, on suppose que la fonction ![]() est définie sur un ensemble
est définie sur un ensemble ![]() et qu’il existe
et qu’il existe ![]() tel que
tel que ![]() .
.
On note ![]() son graphe.
son graphe.
![]() Def1 : Soit
Def1 : Soit ![]() , la fonction
, la fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() si elle vérifie l’une des conditions équivalentes suivantes
si elle vérifie l’une des conditions équivalentes suivantes
![]() tout intervalle ouvert
tout intervalle ouvert ![]() contenant
contenant ![]() contient toutes les valeurs
contient toutes les valeurs ![]() pour
pour ![]() négatif assez grand en valeur absolue
négatif assez grand en valeur absolue
![]() pour tout
pour tout ![]() , il existe
, il existe ![]() tel que si
tel que si ![]() ,
, ![]()
On écrit alors
![]() ou
ou ![]() .
.
![]() Def2 : La fonction
Def2 : La fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() si elle vérifie l’une des deux conditions équivalentes suivantes
si elle vérifie l’une des deux conditions équivalentes suivantes
![]() pour tout
pour tout ![]() , l’intervalle
, l’intervalle ![]() contient toutes les valeurs
contient toutes les valeurs ![]() pour
pour ![]() négatif, assez grand en valeur absolue
négatif, assez grand en valeur absolue
![]() pour tout
pour tout ![]() , il existe
, il existe ![]() tel que si
tel que si ![]() ,
, ![]() .
.
On écrit alors
![]() ou
ou ![]() .
.
![]() Def3 : La fonction
Def3 : La fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() si pour tout
si pour tout ![]() , il existe
, il existe ![]() tel que si
tel que si ![]() ,
, ![]() .
.
On écrit alors
![]() ou
ou ![]() .
.
1.3. Les limites de référence
![]() Pour tout
Pour tout ![]() ,
, ![]()
![]()
![]()
![]() et
et ![]()
![]()
![]()
![]()
![]() et
et ![]() .
.
Vous avez déjà étudié la fonction exponentielle l’an dernier dans le programme de première en maths. Cette année, vous verrez la fonction logarithme avec d’autres limites de référence à connaitre.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. Connaître la définition d’une limite en  d’une fonction
d’une fonction
2.1. Limite à droite en  d’une fonction
d’une fonction
On suppose dans cette partie que ![]() est définie sur un ensemble contenant un intervalle de la forme
est définie sur un ensemble contenant un intervalle de la forme ![]() avec
avec ![]() .
.
![]() On dit que
On dit que ![]() admet
admet ![]() pour limite à droite en
pour limite à droite en ![]() lorsque pour tout
lorsque pour tout ![]() , l’intervalle
, l’intervalle ![]() contient tous les
contient tous les ![]() lorsque
lorsque ![]() est proche de
est proche de ![]() et dans
et dans ![]() .
.
On écrit ![]() .
.
![]() On dit que
On dit que ![]() admet
admet ![]() pour limite à droite en
pour limite à droite en ![]() lorsque pour tout
lorsque pour tout ![]() , l’intervalle
, l’intervalle ![]() contient tous les
contient tous les ![]() lorsque
lorsque ![]() est proche de
est proche de ![]() et supérieur à
et supérieur à ![]() .
.
On écrit ![]() .
.
![]() Soit
Soit ![]() , on dit que
, on dit que ![]() admet
admet ![]() pour limite à droite en
pour limite à droite en ![]() lorsque tout intervalle de la forme
lorsque tout intervalle de la forme ![]() contient tous les
contient tous les ![]() pour
pour ![]() assez proche de
assez proche de ![]() et supérieur à
et supérieur à ![]() .
.
On écrit ![]() .
.
2.2. Limite à gauche en  d’une fonction
d’une fonction
On suppose dans cette partie que ![]() est définie sur un ensemble contenant un intervalle de la forme
est définie sur un ensemble contenant un intervalle de la forme ![]() avec
avec ![]() .
.
On définit comme ci-dessus
![]()
![]()
![]()
![]()
![]()
![]() .
.
en remplaçant « ![]() assez proche de
assez proche de ![]() et supérieur à
et supérieur à ![]() » par «
» par « ![]() assez proche de
assez proche de ![]() et inférieur à
et inférieur à ![]() « .
« .
2.3. Limite en  d’une fonction
d’une fonction
Si ![]() est définie au moins sur
est définie au moins sur ![]() et si les limites de
et si les limites de ![]() à droite et à gauche en
à droite et à gauche en ![]() sont égales à
sont égales à ![]() , on dit que
, on dit que ![]() admet une limite en
admet une limite en ![]() et on écrit
et on écrit ![]() .
.
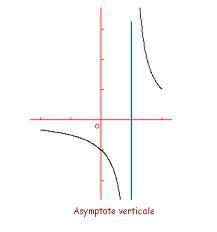
Lorsque ![]() admet une limite (à droite ou à gauche) infinie en
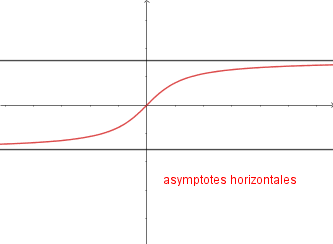
admet une limite (à droite ou à gauche) infinie en ![]() , on dit que la droite d’équation
, on dit que la droite d’équation ![]() est asymptote à la courbe .
est asymptote à la courbe .
Les limites de référence à apprendre par coeur (en début d’année)
![]() ,
, ![]()
![]() .
.
3. Opérations sur les limites
On suppose que les fonctions ![]() et
et ![]() sont définies sur le même ensemble
sont définies sur le même ensemble ![]()
Les limites considérées dans la suite sont prises en ![]() où
où ![]() représente :
représente :
![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() si
si ![]() .
.
On note ![]() et
et ![]() (
(![]() et
et ![]() finies ou infinies)
finies ou infinies)
3.1. Fonction  et limites
et limites
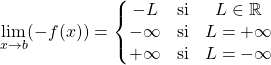
3.2. Somme de limites de fonctions
![]()
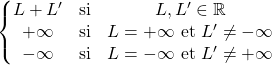
Si ![]() et
et ![]() ,
,
on dit que l’on a une forme indéterminée ![]() .
.
3.3. Produit de limites de fonctions
![]()
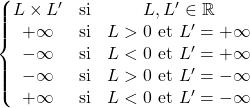
Si ![]() et
et ![]() ,
,
on dit que l’on a une forme indéterminée ![]() .
.
3.4. Inverse et limite d’une fonction
![]() Si
Si ![]() admet en
admet en ![]() une limite infinie ou une limite finie et non nulle, on peut définir
une limite infinie ou une limite finie et non nulle, on peut définir ![]() pour
pour ![]() proche de
proche de ![]() .
.
![]()
![]() Si
Si ![]() admet en
admet en ![]() une limite
une limite ![]()
![]() et si pour
et si pour ![]() proche de
proche de ![]() ,
, ![]() ,
, ![]() .
.
![]() et si pour
et si pour ![]() proche de
proche de ![]() ,
, ![]() ,
, ![]() .
.
3.5. Quotient et limites de fonctions
Pour trouver la limite de ![]() , on cherche avec 3.4., la limite de
, on cherche avec 3.4., la limite de ![]() et on utilise la limite du produit.
et on utilise la limite du produit.
On saura résoudre sauf si
![]()
![]() , on dit que l’on a la forme indéterminée
, on dit que l’on a la forme indéterminée ![]() .
.
![]()
![]() , on dit que l’on a la forme indéterminée
, on dit que l’on a la forme indéterminée ![]() .
.
3.6. Composition et limites de fonctions
On suppose que ![]() sont réels ou égaux à
sont réels ou égaux à ![]() .
.
Soient ![]() et
et ![]() deux fonctions telles que la composée
deux fonctions telles que la composée ![]() soit définie au voisinage de
soit définie au voisinage de ![]() .
.
Si ![]() et
et ![]() ,
,
alors ![]() .
.
Application au changement de variable :
sous réserve d’existence des limites,
![]() En utilisant la fonction
En utilisant la fonction ![]()
![]()
![]()
![]()
![]() .
.
![]() En utilisant la fonction
En utilisant la fonction ![]()
![]() .
.
4. Utilisation d’inégalités et limites en terminale
4.1. Comparaison et limites de fonctions en terminale
![]() F1 Soient
F1 Soient ![]() et
et ![]() deux fonctions définies sur
deux fonctions définies sur ![]() .
.
On suppose que ![]() et
et
pour ![]() ,
, ![]() , alors
, alors ![]() .
.
![]() F1B Soient
F1B Soient ![]() et
et ![]() deux fonctions définies sur
deux fonctions définies sur ![]() .
.
On suppose que ![]() et
et
pour ![]() ,
, ![]() , alors
, alors ![]() .
.
![]() F1T Soient
F1T Soient ![]() et
et ![]() deux fonctions définies dans un même voisinage de
deux fonctions définies dans un même voisinage de ![]()
On suppose que ![]() et
et
pour ![]() proche de
proche de ![]() ,
, ![]() , alors
, alors ![]() .
.
En raisonnant avec ![]() et
et ![]() , on obtient les résultats qui suivent :
, on obtient les résultats qui suivent :
![]() F2 Soient
F2 Soient ![]() et
et ![]() deux fonctions définies sur
deux fonctions définies sur ![]() .
.
On suppose que ![]() et
et
pour ![]() ,
, ![]() , alors
, alors ![]() .
.
![]() F2B Soient
F2B Soient ![]() et
et ![]() deux fonctions définies sur
deux fonctions définies sur ![]() .
.
On suppose que ![]() et
et
pour ![]() ,
, ![]() , alors
, alors ![]() .
.
![]() F2T Soient
F2T Soient ![]() et
et ![]() deux fonctions définies dans un même voisinage de
deux fonctions définies dans un même voisinage de ![]()
On suppose que ![]() et
et
pour ![]() proche de
proche de ![]() ,
, ![]() , alors
, alors ![]() .
.
4.2. Limite par encadrement
C’est le théorème appelé « théorème des gendarmes » par le programme de terminale.
Estimant que les gendarmes ont mieux à faire que de servir de moyen mnémotechnique, j’utiliserai le terme de théorème d’encadrement.
Théorème d’encadrement (ou théorème des gendarmes)
Soit ![]() .
.
Soient ![]() trois fonctions définies sur un intervalle de la forme
trois fonctions définies sur un intervalle de la forme ![]() et vérifiant
et vérifiant
pour tout ![]() ,
, ![]() .
.
Si ![]() , alors
, alors![]() .
.
5. Des limites avec la fonction exponentielle
5.1. Des limites au programme de terminale
![]()
![]() et
et ![]()
![]() Croissance comparée
Croissance comparée
Soit ![]() ,
, ![]() ce qui s’écrit aussi
ce qui s’écrit aussi ![]()
![]() Conséquence :
Conséquence : ![]() .
.
6. Quelques méthodes pour lever des indéterminations
![]() M1 : Pour trouver la limite d’une fonction polynôme en
M1 : Pour trouver la limite d’une fonction polynôme en ![]() , factoriser le terme de plus haut degré.
, factoriser le terme de plus haut degré.
![]() M2 : Pour trouver la limite en
M2 : Pour trouver la limite en ![]() d’un quotient de fonctions polynômes , factoriser au numérateur et au dénominateur le terme de plus haut degré.
d’un quotient de fonctions polynômes , factoriser au numérateur et au dénominateur le terme de plus haut degré.
![]() M3 : En présence de racines carrées, on peut envisager de multiplier et diviser par la quantité conjuguée.
M3 : En présence de racines carrées, on peut envisager de multiplier et diviser par la quantité conjuguée.
![]() M4 : Pour une forme indéterminée avec une exponentielle et un polynôme, chercher à utiliser les résultats sur les croissances comparées.
M4 : Pour une forme indéterminée avec une exponentielle et un polynôme, chercher à utiliser les résultats sur les croissances comparées.
![]() M5 : Pour une forme indéterminée de la forme
M5 : Pour une forme indéterminée de la forme ![]() en
en ![]() pour un quotient de deux fonctions polynômes
pour un quotient de deux fonctions polynômes ![]() et
et ![]() , factoriser
, factoriser ![]() dans les deux fonctions polynômes
dans les deux fonctions polynômes
![]() M6 Reconnaître des taux d’accroissements de fonctions dérivables :
M6 Reconnaître des taux d’accroissements de fonctions dérivables :
![]()
![]()
![]()
![]()
Ce chapitre servira également au moment d’effectuer des calculs de limites de suites en terminale. Complétez vos révisions en consultant et en vous entraînant sur l’ensemble des annales de maths de Terminale mais aussi avec les cours en ligne de maths au programme de Terminale, comme les chapitres suivants :
- la continuité
- l’algorithmique
- les fonctions exponentielles
- les fonctions logarithmes
- les fonctions trigonométriques
Pour des révisions encore plus efficaces et obtenir les meilleurs résultats au bac, n’hésitez pas à prendre des cours particuliers de maths ou effectuer un stage de révisions pendant les vacances.

