Chapitres Maths en Terminale Générale
Cours sur les matrices en Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
A. Définitions des matrices en Terminale
![]() On appelle matrice réelle
On appelle matrice réelle ![]() tout tableau rectangulaire de réels.
tout tableau rectangulaire de réels.
On note ![]() le nombre de lignes de la matrice
le nombre de lignes de la matrice ![]() et
et ![]() le nombre de colonnes de
le nombre de colonnes de ![]() .
.
On dit alors que ![]() est une matrice de type
est une matrice de type ![]() (ou de format
(ou de format ![]() .
.
Dans le cas général pour une matrice ![]() de type
de type ![]() , on note
, on note ![]() le terme dans la ligne numéro
le terme dans la ligne numéro ![]() et dans la colonne numéro
et dans la colonne numéro ![]() lorsque
lorsque ![]() et
et ![]() et on peut écrire
et on peut écrire
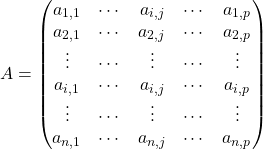
Une matrice ![]() de type
de type ![]() pourra être notée plus simplement
pourra être notée plus simplement
![]() .
.
Une matrice ![]() de type
de type ![]() pourra être notée plus simplement
pourra être notée plus simplement
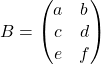 .
.
![]() La matrice de type
La matrice de type ![]() dont tous les éléments sont nuls, est appelée matrice nulle et notée
dont tous les éléments sont nuls, est appelée matrice nulle et notée ![]() . Lorsqu’il n’y a pas de confusion possible, on la note
. Lorsqu’il n’y a pas de confusion possible, on la note ![]() .
.
![]() Lorsque le nombre de lignes est égal au nombre de colonnes de
Lorsque le nombre de lignes est égal au nombre de colonnes de ![]() , on dit que la matrice est une matrice carrée d’ordre
, on dit que la matrice est une matrice carrée d’ordre ![]() (le nombre commun de lignes ou de colonnes). On pourra la noter dans le cas général :
(le nombre commun de lignes ou de colonnes). On pourra la noter dans le cas général :
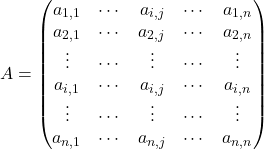
Les termes ![]() forment la diagonale de
forment la diagonale de ![]() .
.
Et simplement,
pour une matrice carrée ![]() d’ordre
d’ordre ![]() ,
,
![]()
et pour une matrice carrée d’ordre ![]() ,
,
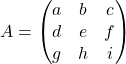 .
.
![]() Lorsque la matrice n’a qu’une ligne ou est de type
Lorsque la matrice n’a qu’une ligne ou est de type ![]() , on dit que c’est une matrice ligne d’ordre
, on dit que c’est une matrice ligne d’ordre ![]() .
.
Elle pourra être notée
![]() .
.
Il suffit de l’écrire ![]() si
si ![]() et
et ![]() si
si ![]() .
.
![]() Lorsque la matrice n’a qu’une colonne (ou est de type
Lorsque la matrice n’a qu’une colonne (ou est de type ![]() ), on dit que c’est une matrice colonne d’ordre
), on dit que c’est une matrice colonne d’ordre ![]() .
.
Une matrice ![]() colonne d’ordre
colonne d’ordre ![]() pourra donc être notée
pourra donc être notée
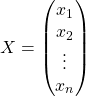 .
.
Avec les notations plus simples, ![]() pour une matrice colonne d’ordre
pour une matrice colonne d’ordre ![]() et
et 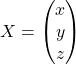 pour une matrice colonne d’ordre 3.
pour une matrice colonne d’ordre 3.
Si vous avez des difficultés en mathématiques, nous mettons à disposition des cours de soutien de maths adaptés aux étudiants en terminale.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
B. Premières opérations sur les matrices en Terminale
1. Produit d’une matrice par un réel
Si ![]() est une matrice de type
est une matrice de type ![]() et si
et si ![]() est un réel, on note
est un réel, on note ![]() la matrice de type
la matrice de type ![]() obtenue en multipliant chaque terme de la matrice
obtenue en multipliant chaque terme de la matrice ![]() par le réel
par le réel ![]() .
.
propriétés :
Si ![]() ,
, ![]() est la matrice nulle (de même type que
est la matrice nulle (de même type que ![]() ).
).
Si ![]() , la matrice
, la matrice ![]() est notée
est notée ![]() et appelée matrice opposée de
et appelée matrice opposée de ![]() .
.
Pour tout réel ![]() , si
, si ![]() est la matrice nulle,
est la matrice nulle, ![]() .
.
2. Addition de deux matrices en Maths expertes
![]() Si
Si ![]() et
et ![]() sont deux matrices de même type
sont deux matrices de même type ![]() ,
,
![]() est la matrice de type
est la matrice de type ![]() dont l’élément en ligne
dont l’élément en ligne ![]() et colonne
et colonne ![]() est la somme de
est la somme de ![]() et de
et de ![]() .
.
Si ![]()
et ![]()
![]() .
.
3. Propriétés de deux matrices
![]() Les matrices
Les matrices ![]() et
et ![]() étant de même format
étant de même format ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]() Si
Si ![]() ,
, ![]() .
.
![]() On définit la différence des deux matrices
On définit la différence des deux matrices ![]() et
et ![]() par
par ![]() et on la note
et on la note ![]()
l’élément en ligne ![]() et colonne
et colonne ![]() est égal à
est égal à ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
C. Produit matriciel en Terminale
1. Produit d’une matrice par une matrice colonne
On commence par des cas particuliers
![]()
![]() et
et ![]()
![]() est une matrice colonne à 2 lignes donnée par
est une matrice colonne à 2 lignes donnée par
![]()
![]()
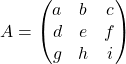 et
et 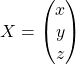
![]() est une matrice colonne à 3 lignes donnée par
est une matrice colonne à 3 lignes donnée par
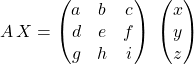
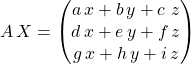 .
.
2. Produit de deux matrices carrées de même ordre
Si ![]() et
et ![]() sont deux matrices carrées d’ordre
sont deux matrices carrées d’ordre ![]() , on peut définir le produit
, on peut définir le produit ![]() et on obtient une matrice carrée d’ordre
et on obtient une matrice carrée d’ordre ![]() .
.
![]() On commence par le cas d’un produit de deux matrices carrées d’ordre
On commence par le cas d’un produit de deux matrices carrées d’ordre ![]()
![]() et
et ![]()
![]() .
.
![]() Pour le produit de deux matrices carrées d’ordre 3 :
Pour le produit de deux matrices carrées d’ordre 3 :
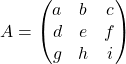
et 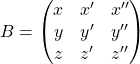
![]() est égale à
est égale à
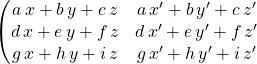
et sa troisième colonne est
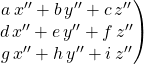
Le terme en ligne ![]() et colonne
et colonne ![]() s’obtient en multipliant la ligne
s’obtient en multipliant la ligne ![]() de
de ![]() par la colonne
par la colonne ![]() de
de ![]() .
.
3. Produit d’une matrice ligne par une matrice en Terminale
![]() Si
Si ![]() est une matrice carrée d’ordre 2 et
est une matrice carrée d’ordre 2 et ![]() une matrice ligne à deux colonnes,
une matrice ligne à deux colonnes,
![]() est une matrice ligne à deux colonnes
est une matrice ligne à deux colonnes
![]()
![]() .
.
![]() Si
Si ![]() est une matrice carrée d’ordre 3 et
est une matrice carrée d’ordre 3 et ![]() une matrice ligne à trois colonnes,
une matrice ligne à trois colonnes,
![]() est une matrice ligne à trois colonnes
est une matrice ligne à trois colonnes
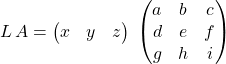
![]()
![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
D. Propriétés du produit matriciel en Terminale en Maths Expertes
1. Propriétés du produit matriciel en Maths Expertes
![]() Sous réserve de définition de la somme et du produit,
Sous réserve de définition de la somme et du produit,
pour toutes matrices ![]() ,
, ![]() et
et ![]() et tout réel
et tout réel ![]() ,
,
![]()
![]() que l’on note
que l’on note ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]() de type
de type ![]() ,
, ![]()
et ![]() .
.
2. Matrices identité d’ordre  ,
,
![]() Soit
Soit ![]() . On note
. On note ![]() la matrice carrée d’ordre
la matrice carrée d’ordre ![]() , dont tous les termes sont nuls sauf les termes de la diagonale (soit d’indices
, dont tous les termes sont nuls sauf les termes de la diagonale (soit d’indices ![]() ) sont égaux à
) sont égaux à ![]() . On l’appelle matrice identité d’ordre
. On l’appelle matrice identité d’ordre ![]() .
.
![]() et
et 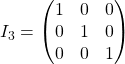 .
.
![]() Sous réserve que les produits soient définis,
Sous réserve que les produits soient définis, ![]() et
et ![]()
donc si ![]() est carrée d’ordre
est carrée d’ordre ![]() ,
, ![]() .
.
3. Matrice inversible en terminale générale
![]() Soit
Soit ![]() une matrice carrée d’ordre
une matrice carrée d’ordre ![]() . S’il existe deux matrices
. S’il existe deux matrices ![]() et
et ![]() carrées d’ordre
carrées d’ordre ![]() telles que
telles que ![]() et
et ![]() , alors
, alors ![]() .
.
![]() Soit
Soit ![]() une matrice carrée d’ordre
une matrice carrée d’ordre ![]() . On dit que
. On dit que ![]() est une matrice inversible lorsqu’il existe une matrice
est une matrice inversible lorsqu’il existe une matrice ![]() carrée d’ordre
carrée d’ordre ![]() telle que
telle que ![]() et
et ![]() .
.
Dans ce cas, la matrice ![]() est unique et on l’appelle matrice inverse de la matrice
est unique et on l’appelle matrice inverse de la matrice ![]() et on note
et on note ![]() .
.
![]() Soit
Soit ![]() une matrice carrée d’ordre
une matrice carrée d’ordre ![]() inversible et
inversible et ![]() et
et ![]() deux matrices de type
deux matrices de type ![]() ,
,
![]() ssi
ssi ![]() .
.
4. Puissance  -ième d’une matrice carrée
-ième d’une matrice carrée  d’ordre
d’ordre  .
.
![]() Si
Si ![]() est une matrice carrée d’ordre
est une matrice carrée d’ordre ![]() , on définit
, on définit
![]() et si
et si ![]() ,
, ![]() .
.
Si ![]() et
et ![]() ,
, ![]() est le produit de
est le produit de ![]() matrices
matrices ![]() et
et ![]() .
.
![]() Si
Si ![]() est une matrice carrée et si
est une matrice carrée et si ![]() ,
, ![]() .
.
![]() Si
Si ![]() est une matrice carrée diagonale et
est une matrice carrée diagonale et ![]() ,
,
![]()
![]() ,
, ![]() .
.
![]()
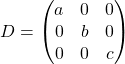
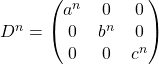 .
.
Ce sera en particulier simple
![]() lorsque
lorsque ![]() ,
,
il faudra prouver que ![]() lorsque
lorsque ![]() .
.
![]() lorsque
lorsque ![]() ,
,
il faudra alors prouver que ![]() et
et ![]() si
si ![]() .
.
![]() Dans certains cas, on peut trouver une relation de récurrence vérifiée par les coefficients
Dans certains cas, on peut trouver une relation de récurrence vérifiée par les coefficients ![]() etc de la matrice
etc de la matrice ![]() .
.
Les mathématiques sont une matière très difficile et le programme de maths expertes est quant à lui encore plus difficile. N’accumulez pas les lacunes et relisez régulièrement vos cours de maths pour être certain d’avoir assimilé les notions essentielles de chaque chapitre. Quelques cours à bien revoir avant le bac :

