Chapitres Maths en Terminale Générale
Cours sur la fonction polynome en Terminale Générale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
A. Généralités sur la fonction polynome en Terminale
![]() On dit que
On dit que ![]() est une fonction polynôme à coefficients réels lorsqu’il existe un entier
est une fonction polynôme à coefficients réels lorsqu’il existe un entier ![]() et des réels
et des réels ![]()
![]() tels que pour tout réel
tels que pour tout réel ![]() ,
,
![]()
![]() .
.
Si de plus ![]() , on dit que
, on dit que ![]() est une fonction polynôme de degré
est une fonction polynôme de degré ![]() .
.
Pour tout réel ![]() ,
, ![]() .
.
On écrit aussi 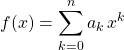 .
.
On peut aussi dire que ![]() est un polynôme.
est un polynôme.
![]() La fonction polynome
La fonction polynome
![]()
![]()
est la fonction nulle ssi ![]() .
.
![]() Si
Si ![]() et
et ![]() sont des fonctions polynômes,
sont des fonctions polynômes, ![]() et
et ![]() sont des fonction polynômes.
sont des fonction polynômes.
On peut en effet trouver ![]() et des réels
et des réels ![]() et
et ![]() tels que
tels que
![]() et
et ![]()
et alors
![]()
![]()
![]()
![]()
avec les notations précédentes
![]() ssi
ssi ![]() et
et ![]() .
.
![]() Si
Si ![]() est une fonction polynôme à coefficients réels et
est une fonction polynôme à coefficients réels et ![]() ,
, ![]() est une fonction polynome de même degré que
est une fonction polynome de même degré que ![]() si
si ![]() et
et ![]() .
.
![]() Si
Si ![]() et
et ![]() sont deux fonctions polynômes de degrés respectifs
sont deux fonctions polynômes de degrés respectifs ![]() et
et ![]() ,
, ![]() est une fonction polynôme de degré
est une fonction polynôme de degré ![]() .
.
N’hésitez pas retrouver nos profs de maths sur notre plateforme en cas de besoin sur le chapitre des polynômes.
Mon parcours pour réussir en Terminale
Je révise le bac en autonomie ou avec un prof
J'obtiens des conseils d'orientation
Je m’entraîne sur des annales corrigées du bac
Avis Google France
★★★★★ 4,8 sur 5
B. Équations polynomiales particulières en Terminale
1. Équation du second degré à coefficients réels
Soit ![]()
une fonction polynome du second degré à coefficients réels
Lorsque ![]() , on peut écrire
, on peut écrire ![]()
L’équation ![]() admet deux racines complexes conjuguées :
admet deux racines complexes conjuguées :
![]()
![]() .
.
Somme et produit :
![]() et
et ![]() .
.
Si ![]() , vous pouvez écrire
, vous pouvez écrire ![]() avec
avec ![]() et écrire les racines sous la forme
et écrire les racines sous la forme ![]() .
.
2. Factorisation de 
Pour ![]() et
et ![]() réels ou complexes et
réels ou complexes et ![]()
![]()
![]()
![]()
Soit 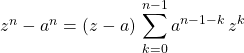 .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
C. Racines d’une fonction polynome en Terminale
1. Résultats généraux des racines d’une fonction polynome
![]() Th1 : Soit
Th1 : Soit ![]() et
et ![]() une fonction polynôme à coefficients réels.
une fonction polynôme à coefficients réels.
Il existe une fonction polynôme ![]() à coefficients réels telle que
à coefficients réels telle que ![]() ssi
ssi ![]() .
.
On dit que ![]() est racine de la fonction polynome
est racine de la fonction polynome ![]() .
.
![]() Th2 :
Th2 : ![]() Soit
Soit ![]() une fonction polynôme et
une fonction polynôme et ![]() des racines distinctes de
des racines distinctes de ![]() .
.
Il existe une fonction polynôme ![]() telle que pour tout réel
telle que pour tout réel ![]() ,
,
![]() .
.
![]() Th3 : Une fonction polynome
Th3 : Une fonction polynome ![]() de degré
de degré ![]() admet au plus
admet au plus ![]() racines distinctes réelles.
racines distinctes réelles.
2. Cas d’une fonction polynôme de degré 3
Soit ![]() une fonction polynome à coefficients réels de degré 3 et
une fonction polynome à coefficients réels de degré 3 et ![]() tel que
tel que ![]() .
.
Il existe des réels ![]() et
et ![]() tels que
tels que
![]()
avec ![]()
Le programme de Maths Expertes en terminale est très exigeant, soyez donc certains de vos connaissances sur tous les chapitres du programme en travaillant avec les cours en ligne suivants :
- géométrie et complexes
- arithmétique – congruences
- l’arithmétique – PGCD PPCM
- arithmétique – nombres premiers et Fermat
- matrices
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut


