Chapitres Maths en Terminale Générale

Cours, exercices et corrigés sur : Loi à densité

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Résumé de cours sur les lois à densité en terminale

Révisez votre cours de maths au programme de terminale sur les lois à densité et exercez-vous sur les exercices corrigés ci-dessous. Pour réussir au bac et réussir en terminale, il est primordial de bien connaître tous les chapitres du programme de maths de terminale. Aucune impasse ne doit être faite lors de votre préparation au bac. En effet, certains exercices demandent parfois d’utiliser des notions issues de plusieurs chapitres pour résoudre l’exercice. Pour maximiser vos chances de réussite, il est recommandé de prendre des cours particuliers en maths.

1. Variable aléatoire discrète

Définition: variable aléatoire discrète

On dit qu’on définit une variable aléatoire discrète $X$ sur l’ensemble $E$ lorsque, à chaque éventualité $e$ de l’expérience aléatoire, on associe un nombre réel $X(e)\text{ : }e \longmapsto X(e)$ .

Notations :

Les événements sont des sous-ensembles de $E$ . Dans le cas général, la notation $(X=a)$ , avec $a \in \mathbb{R}$ , désigne l’événement $\left\{ e \in E\text{ }|\text{ }X(e) = a \right\}$ , i.e l’ensemble des éventualités $e$ pour lesquelles la variable aléatoire $X$ prend la valeur $a$ .

Définition: loi de probabilité discrète

La loi de probabilité d’une variable aléatoire discrète $X$ est donnée par :

$\bullet$ l’ensemble des valeurs $\{x_{1},...,x_{n}\}$ prises par la variable aléatoire;

$\bullet$ les probabilités $P(X=x_{i})$ pour toutes les valeurs $x_{i}$ prises par $X$ .

On rappelle que:

$\sum_{i=1}^{n} P(X=x_{i}) = 1$

Définition: espérance d’une variable aléatoire discrète

Si l’on considère une variable aléatoire discrète $X$ qui prend les valeurs $\{x_{1},...,x_{n}\}$ avec les probabilités $P(X=x_{i})$ , son espérance, lorsqu’elle existe, est définie par la relation:

$\boxed{E(X) = \sum_{i=1}^{n} x_{i} \times P(X=x_{i})}$

Remarque. Toutes les variables aléatoires n’admettent pas une espérance.

Propriété: linéarité de l’espérance

L’espérance est linéaire: soient $X$ et $Y$ deux variables aléatoires discrètes à valeurs réelles qui admettent toutes deux une espérance, et $\lambda \in \mathbb{R}$ . Alors $X + \lambda Y$ admet également une espérance, et nous avons:

$\boxed{E(X + \lambda Y) = E(X) + \lambda E(Y)}$

Définition: variance d’une variable aléatoire discrète

Si l’on considère une variable aléatoire discrète $X$ qui prend les valeurs $\{x_{1},...,x_{n}\}$ avec les probabilités $P(X=x_{i})$ , sa variance, lorsqu’elle existe, est définie par la relation:

$\boxed{Var(X) = E\left[\left(X-E(X)\right)^{2}\right]}$

La racine carrée de la variance est appelé écart-type, noté $\sigma(X)$ :

$\boxed{\sigma(X) = \sqrt{Var(X)}}$

Remarque. Toutes les variables aléatoires n’admettent pas une variance.

Propriétés

$\bullet$ On monte que:

$\boxed{Var(X) = E(X^{2}) - E(X)^{2}}$

$\bullet$ Soient $X_{1}, ..., X_{n}$ des variables aléatoires qui admettent une variance. Alors $X = \sum_{i=1}^{n} X_{i}$ admet également une variance, et nous avons:

Si les $X_{i}$ sont indépendantes:

$Var(X) = Var\left(\sum_{i=1}^{n} X_{i}\right)$

$= \sum_{i=1}^{n} Var(X_{i})$

COURS PARTICULIERS

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

96% de réussite au BAC
44% de mentions Bien et Très bien
99% de recommandation à leurs amis

POUR ACCÉLÉRER MA PROGRESSION EN TERMINALE

Avis Google France ★★★★★ 4,9 sur 5

2. Lois de probabilités à densité sur un intervalle

Définitions et propriétés

Définition : densité de probabilité

On dit qu’une fonction f, définie sur un intervalle $I$ de $\mathbb{R}$ , est une densité de probabilité sur $I$ lorsque :

$\bullet$ la fonction $f$ est continue sur $I$ ;

$\bullet$ la fonction $f$ est à valeurs positives sur $I$ ;

$\bullet$ l’aire sous la courbe de $f$ est égale à $1$ unités d’aire.

Définition: variable aléatoire à densité

Soit $f$ une fonction définie sur $I$ , qui est une densité de probabilité sur $I$ .

On dit que la variable aléatoire $X$ suit la loi de densité $f$ sur l’intervalle $I$ (ou est « à densité $f$ sur $I$ « ) lorsque, pour tout intervalle $J$ inclus dans $I$ , la probabilité de l’événement $(X \in J)$ est la mesure, en unités d’aire, de l’aire du domaine: $\left\{M(x,y)\text{ }|\text{ }x \in J\text{ et }0 \leq y\leq f(x)\right\}$ .

$\boxed{\forall J \subset I\text{, }P(X \in J) = \int_{t \in J} f(t)\text{ } dt}$

Propriétés

Soit $X$ une variable aléatoire qui suit la loi de densité $f$ sur l’intervalle $I$ . On a les propriétés suivantes :

$\bullet$ Si $J$ et $J'$ sont deux unions finies d’intervalles inclus dans $I$ , on a :

$\bullet$ Pour tout intervalle $J = [c;d]$ de $I$ , on a :

$\boxed{P(X \in J) = P(c \leq X \leq d) = \int_{c}^{d} f(t)\text{ } dt}$

$\bullet$ Pour tout réel $\alpha$ de $I$ , on a : $P(X=\alpha)=0$ .

$\bullet$ Pour tous réels $c$ et $d$ de $I$ :

$P(c \leq X \leq d) = P(c < X \leq d)$

$= P(c \leq X < d) = P(c < X < d)$

$\bullet$ Soit $J$ un intervalle inclus dans $I$ , on a : $P(X \in \overline{J}) = 1 - P (X \in J)$

Définition: probabilité conditionnelle

Soit $I'$ un intervalle de $I$ tel que $P(X \in I') \neq 0$ et soit $J$ un autre intervalle de $I$ . On définit la probabilité conditionnelle $P_{X \in I'}(X \in J)$ par l’égalité :

$\boxed{P_{X \in I'}(X \in J) = \frac{P(X \in I' \cap J)}{P(X \in I')}}$

Définition: espérance d’une variable aléatoire à densité

L’espérance $E(X)$ d’une variable aléatoire à densité $f$ sur $[a;b]$ est définie par:

$\boxed{E(X) = \int_{a}^{b} xf(x)\text{ } dx}$

Loi uniforme sur $[0,1]$

Propriété

La fonction constante $f$ définie sur $[0;1]$ par $f(x)=1$ est une densité de probabilité.

Définition: loi uniforme sur $[0;1]$

On dit qu’une variable aléatoire $X$ suit la loi uniforme sur l’intervalle $[0;1]$ si sa densité est la fonction définie sur $[0;1]$ par:

$\boxed{f\text{ : }x \in [0;1] \longmapsto f(x) = 1}$

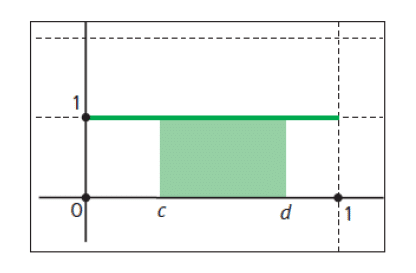
Densité de probabilité de la loi uniforme sur $[0;1]$

Propriété

Pour tout intervalle $[c;d]$ inclus dans $[0;1]$ , on a :

$\boxed{P(X \in [c;d]) = P(c \leq X \leq d) = d-c}$

Loi uniforme sur $[a;b]$

Propriété

La fonction constante $f$ définie sur $[a;b]$ , avec $a < b$ , par $f(x)=\frac{1}{b-a}$ est une densité de probabilité.

Définition: loi uniforme sur $[a;b]$

Une variable aléatoire $X$ suit une loi uniforme sur l’intervalle $[a;b]$ $(a < b)$ si sa densité est la fonction $f$ définie sur $[a;b]$ par:

$\boxed{f\text{ : }x \in [a;b] \longmapsto f(x) = \frac{1}{b-a}}$

Propriété

Pour tout intervalle $[c;d]$ inclus dans $[0;1]$ , on a :

$\boxed{P(X \in [c;d]) = P(c \leq X \leq d) = \frac{d-c}{b-a}}$

Propriété: espérance d’une loi uniforme sur $[a;b]$

L’espérance $E(X)$ d’une variable aléatoire $X$ suivant une loi uniforme sur $[a;b]$ est telle que:

$\boxed{E(X) = \int_{a}^{b} xf(x)\text{ } dx = \frac{a+b}{2}}$

STAGE REVISION BAC

Profite de tes vacances pour gagner des points au bac.

96% de réussite au BAC
44% de mentions Bien et Très bien
99% de recommandation à leurs amis

Avis Google France ★★★★★ 4,9 sur 5

Loi exponentielle

Propriété

Soit $\lambda$ un nombre réel strictement positif. La fonction $f$ définie sur $I = [0;+\infty[$ par

$f\text{ : }t \in [0;+\infty[ \longmapsto f(t) = \lambda e^{-\lambda t}$

est une densité de probabilité.

Définition: loi exponentielle de paramètre $\lambda \in \mathbb{R}_{+}^{*}$

Soit $\lambda$ un nombre réel strictement positif. Une variable aléatoire à densité $X$ suit la loi exponentielle de paramètre $\lambda$ si sa densité est la fonction $f$ définie sur $[0;+\infty[$ par:

$\boxed{f\text{ : }t \in [0;+\infty[ \longmapsto f(t) = \lambda e^{-\lambda t}}$

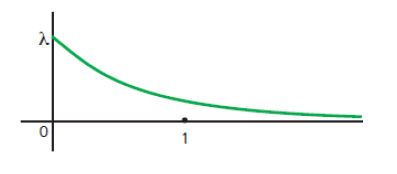
Densité de probabilité de la loi exponentielle de paramètre $\lambda >0$

Remarque. Le paramètre $\lambda$ est égal à l’ordonnée du point de la courbe représentant la densité situé sur l’axe des ordonnées car $f(0) = \lambda e^{0} = \lambda$ .

Propriété

Soit $X$ une variable aléatoire à densité qui suit la loi exponentielle de paramètre $\lambda > 0$ .

$\bullet$ Quels que soient les nombres réels positifs $c$ et $d$ , on a :

$P(X \in [c;d]) = P(c \leq X \leq d)$

$= \int_{c}^{d} \lambda e^{-\lambda t}\text{ } dt = e^{-\lambda c} - e^{-\lambda d}$

$\bullet$ Pour tout réel positif $a$ , on a: $\boxed{P(X \geq a)= e^{-\lambda a}}$

Définition: espérance d’une loi exponentielle

On définit l’espérance $E(X)$ d’une variable aléatoire suivant la loi exponentielle de paramètre $\lambda \in \mathbb{R}_{+}^{*}$ en posant:

$\boxed{E(X) = \lim_{x \longrightarrow +\infty} \int_{0}^{x} t\text{ }\lambda e^{-\lambda t}\text{ } dt}$

Propriété

L’espérance $E(X)$ d’une variable aléatoire suivant la loi exponentielle de paramètre $\lambda \in \mathbb{R}_{+}^{*}$ est telle que:

$\boxed{E(X) = \frac{1}{\lambda}}$

Propriété: durée de vie sans vieillissement

Une variable aléatoire $X$ qui suit une loi exponentielle est telle que, pour tous réels $x$ et $h$ positifs, on a:

$\boxed{P_{X \geq t}(X \geq t+h) = P(X \geq h)}$

Cette propriété est appelée propriété de durée de vie sans vieillissement. En effet, si on interprète X comme la durée de vie d’un appareil, cette égalité signifie que la probabilité que l’appareil fonctionne encore au-delà du temps $t+h$ sachant qu’il fonctionne encore à l’instant $t$ est égale à la probabilité que l’appareil fonctionne au-delà du temps $h$ . Cela signifie que, pendant l’intervalle $[0;t]$ , l’appareil ne s’est pas usé puisque son fonctionnement à partir de l’instant $t$ est identique à celui qu’il avait à partir du temps $0$ .

Pour accéder aux cours complets, annales et aux corrigés de tous les exercices

Télécharge gratuitement PrepApp

Exercices de probabilités : Loi à densité, loi normale et estimation

Les exercices sur les probabilités : Loi à densité, loi normale, fluctuations et estimation arrivent sous peu.

Annales de probabilités : Loi à densité, fluctuations et estimation

Pour avoir un bon niveau de maths, il faut tout simplement réviser régulièrement, mais aussi, et surtout, s’entraîner et se tester sur divers exercices de maths, comme sur les annales de bac de maths. Les annales du bac sont les meilleurs exercices puisque ce sont des sujets déjà tombés lors de l’examen. Les élèves de terminale peuvent donc se rendre compte du niveau attendu le jour de l’examen, mais aussi des exigences et du système de notation de l’épreuve. Il est également possible pour les élèves de terminale de participer à des stages intensifs en terminale pour se préparer aux épreuves du bac. Grâce à ces stages, les élèves pourront décrocher les notes attendues et espérées via le simulateur de bac.

Les élèves de terminale qui suivent l’option maths complémentaires en terminale générale devront également être parfaitement à l’aise sur les chapitres suivants :

les suites numériques et les modèles discrets
les fonctions convexes
les lois discrètes
les statistiques à 2 variables aléatoires

Cours, exercices et corrigés sur : Loi à densité

Résumé de cours sur les lois à densité en terminale

1. Variable aléatoire discrète

COURS PARTICULIERS

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION EN TERMINALE

2. Lois de probabilités à densité sur un intervalle

STAGE REVISION BAC

Profite de tes vacances pour gagner des points au bac.

Pour accéder aux cours complets, annales et aux corrigés de tous les exercices

Télécharge gratuitement PrepApp

Exercices de probabilités : Loi à densité, loi normale et estimation

Annales de probabilités : Loi à densité, fluctuations et estimation

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales