Chapitres Maths en Terminale Générale
Limites de fonction exercices et corrigés Terminale
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Terminale
Préparez vos révisions en vous exerçant sur nos exercices de mathématiques sur le chapitre des limites de fonction en Terminale. N’hésitez pas à compléter avec les annales de bac en Terminale en maths pour asseoir durablement vos connaissances. Ce chapitre est très important pour la suite de l’année car dans toute étude de fonction exponentielle ou encore de fonction logarithme en terminale, il y aura forcément un calcul de limite à effectuer. Par ailleurs, vous pouvez aussi faire appel à un prof particulier en maths pour comprendre et maîtriser les limites de fonction et réussir le bac.
1. Calcul de limites : exercices corrigés
Consignes :
![]() Lorsque le problème mettra en évidence une asymptote horizontale ou verticale, on précisera son équation.
Lorsque le problème mettra en évidence une asymptote horizontale ou verticale, on précisera son équation.
![]() On répondra
On répondra
![]() +oo , -oo pour une limite égale à
+oo , -oo pour une limite égale à ![]() ,
, ![]()
![]() a/b pour une limite égale à
a/b pour une limite égale à ![]()
![]() Pour « limite à gauche, à droite » : donner les 2 limites séparées par une virgule, sans espace
Pour « limite à gauche, à droite » : donner les 2 limites séparées par une virgule, sans espace
Exercice 1 : Limites en 
Déterminer les limites suivantes en ![]() ou
ou![]() selon le cas.
selon le cas.
Question 1 :
En ![]() ,
, ![]()
Question 2 :
En ![]() ,
, ![]()
Question 3 :
En ![]() ,
, ![]()
Question 4 :
a) En ![]() ,
, ![]()
b) En ![]() ,
, ![]() .
.
Question 5 :
En ![]() ,
, ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice 1 sur les Limites en  :
:
Question 1 :
Limite : -3
On a une forme indéterminée ![]()
Car la limite d’une fonction polynôme en ![]() est la limite du terme de plus haut degré .
est la limite du terme de plus haut degré .
On factorise ![]() au numérateur et
au numérateur et ![]() au dénominateur de la fraction
au dénominateur de la fraction
![]()
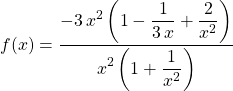
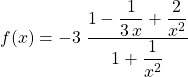 .
.
Comme ![]()
et ![]() ,
,
On en déduit que ![]() .
.
Remarque : on démontre de même que ![]() .
.
On aurait aussi pu factoriser ![]() au lieu de
au lieu de ![]() au numérateur.
au numérateur.
Question 2 :
Limite : -oo
On a une forme indéterminée ![]()
car la limite d’une fonction polynôme en ![]() est la limite du terme de plus haut degré .
est la limite du terme de plus haut degré .
On factorise ![]() au numérateur et
au numérateur et ![]() au dénominateur
au dénominateur
![]()
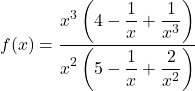
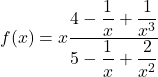
Comme ![]()
et ![]() ,
,
On en déduit que 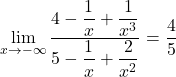
Et comme ![]() ,
,
![]() .
.
On démontre de même que ![]() .
.
Question 3 :
Limites : 0
On a une forme indéterminée ![]()
car la limite d’une fonction polynôme en ![]() est la limite du terme de plus haut degré .
est la limite du terme de plus haut degré .
On factorise ![]() au numérateur et
au numérateur et ![]() au dénominateur
au dénominateur
![]()
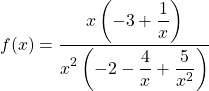
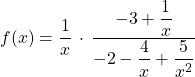
Comme ![]()
et ![]() ,
,
on en déduit que 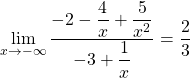 .
.
Et comme ![]() ,
, ![]() .
.
On démontre de même que ![]() .
.
Question 4 :
a : Limite : +oo
![]()
et ![]()
donc ![]() .
.
b : Limite : 0
![]()
![]()
et ![]()
on a une forme indéterminée ![]() .
.
![]() On utilise la quantité conjuguée
On utilise la quantité conjuguée
![]()
![]()
![]()
comme ![]() (somme de deux fonctions de limite
(somme de deux fonctions de limite ![]() ),
), ![]() .
.
On obtient une asymptote horizontale d’équation ![]() en
en ![]() .
.
La courbe est située en dessous de son asymptote car ![]() .
.
Question 5 :
Limite : 1/2
![]()
![]()
et ![]() ,
,
on a une forme indéterminée ![]() .
.
![]() On utilise la quantité conjuguée
On utilise la quantité conjuguée
![]()
![]()
![]()
![]() (par somme de deux fonctions de limite égale à
(par somme de deux fonctions de limite égale à ![]() ) et on a une forme indéterminée
) et on a une forme indéterminée ![]() .
.
![]() On factorise
On factorise ![]() au dénominateur
au dénominateur
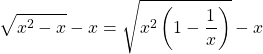
en faisant attention que ![]() , donc
, donc ![]() ,
,
![]()
on peut alors simplifier le quotient :
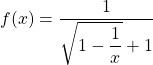
comme 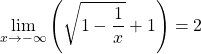 alors
alors ![]() .
.
On obtient une asymptote horizontale d’équation ![]() en
en ![]() .
.
Exercice 2 : Limites en 0
Question 1 :
En ![]() ,
, ![]()
Question 2 :
En ![]() ,
, ![]()
Question 3 :
En ![]() ,
, ![]()
Correction de l’exercice 2 sur les limites en 0 en Terminale :
Question 1 :
limite à gauche, à droite : -1,1
![]()
On a une forme indéterminée ![]() .
.
Si ![]() ,
, ![]()
Si ![]() ,
, ![]()
![]() et
et ![]() .
.
Question 2 :
limite : -1
![]() On a une forme indéterminée
On a une forme indéterminée ![]() :
:
![]()
![]() .
.
![]() On utilise la quantité conjuguée du numérateur et dénominateur :
On utilise la quantité conjuguée du numérateur et dénominateur :
![]()
![]()
on simplifie par ![]()
![]()
![]()
![]()
Par quotient des limites,
![]()
![]() .
.
Question 3 :
limite : 3
Utiliser un taux d’accroissement.
C’est une forme indéterminée ![]() .
.
On note ![]()
![]()
c’est le taux d’accroissement de ![]() en
en ![]() , comme
, comme ![]() est dérivable,
est dérivable,
![]()
![]()
On a utilisé
![]() si
si ![]() est dérivable sur
est dérivable sur ![]() et si
et si ![]() et
et ![]() sont réels,
sont réels, ![]() est dérivable sur
est dérivable sur ![]() et
et ![]()
![]() et
et ![]() a pour dérivée
a pour dérivée ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Exercice 3 : Limite en 
Question 1 :
En ![]() ,
, ![]()
Question 2 :
En ![]() ,
, ![]()
Question 3 :
En ![]() ,
, ![]()
Corrigé de l’exercice 3 sur les limites en  en Terminale :
en Terminale :
Question 1 :
limite à gauche, à droite : +oo,-oo
![]()
![]()
![]() et
et ![]()
donc ![]()
alors ![]() .
.
![]()
![]() et
et ![]()
donc ![]()
alors ![]() .
.
On obtient une asymptote verticale d’équation ![]()
Question 2 :
limite à gauche, à droite : -oo,-oo
![]() et
et ![]() ,
,
![]() .
.
![]() ,
,
donc 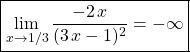 .
.
La droite verticale d’équation ![]() est asymptote à la courbe.
est asymptote à la courbe.
Question 3 :
limite à gauche, à droite : +oo,-oo
![]() .
.
![]()
![]() et
et ![]()
donc ![]()
alors 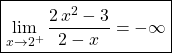 .
.
![]()
![]() et
et ![]()
donc ![]()
alors 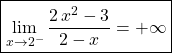 .
.
On obtient une asymptote verticale d’équation ![]() .
.
2. Limites de fonction et suites : exercices corrigés
Question 1 :
![]() Soit
Soit ![]() admettant une limite
admettant une limite ![]() (finie ou infinie) en
(finie ou infinie) en ![]() .
.
Pour toute suite ![]() de
de ![]() telle que
telle que ![]() ,
, ![]() .
.
Corrigés limites de fonction de la question 1 :
![]() Démonstration dans le cas où
Démonstration dans le cas où ![]()
![]() On introduit un intervalle
On introduit un intervalle ![]() ouvert quelconque contenant
ouvert quelconque contenant ![]() .
.
Par définition de ![]() ,
,
il existe ![]() tel que si
tel que si ![]() ,
, ![]()
![]() Comme
Comme ![]() , à partir d’un certain rang
, à partir d’un certain rang ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() Ayant prouvé que pour tout intervalle
Ayant prouvé que pour tout intervalle ![]() ouvert quelconque contenant
ouvert quelconque contenant ![]() , il existe un rang
, il existe un rang ![]() entier tel que si
entier tel que si ![]() ,
, ![]() , on a donc prouvé que
, on a donc prouvé que ![]()
![]() Démonstration dans le cas où
Démonstration dans le cas où ![]()
![]() Soit
Soit ![]() .
.
Par définition de ![]()
il existe ![]() tel que si
tel que si ![]() ,
, ![]()
![]() Comme
Comme ![]() , à partir d’un certain rang
, à partir d’un certain rang ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() Ayant prouvé que pour tout
Ayant prouvé que pour tout ![]() , il existe un rang
, il existe un rang ![]() entier tel que si
entier tel que si ![]() ,
, ![]() , on a donc prouvé que
, on a donc prouvé que ![]() .
.
![]() Dans le cas où
Dans le cas où ![]() , il suffit d’appliquer le résultat précédent à la fonction
, il suffit d’appliquer le résultat précédent à la fonction ![]() .
.
3. Étude complète d’une fonction en Terminale
On note ![]() .
.
Question 1 :
Étude des branches infinies
Question 2 :
Étude des variations de ![]()
Question 3 :
Tableau de variation et graphe
Correction de l’exercice :
Question 1 :
![]() est définie sur
est définie sur ![]() .
.
![]() Étude en
Étude en ![]()
![]()
![]()
![]() et
et ![]() , donc
, donc ![]() .
.
![]()
![]() et
et ![]() , donc
, donc ![]() .
.
La droite d’équation ![]() est asymptote à la courbe.
est asymptote à la courbe.
![]() Limites en
Limites en ![]()
On lève l’indétermination ![]() en factorisant
en factorisant ![]() au numérateur et
au numérateur et ![]() au dénominateur
au dénominateur
![]()
![]()
comme ![]()
et ![]()
alors ![]()
![]() et
et ![]() .
.
![]() Étude de la branche infinie en
Étude de la branche infinie en ![]()
![]() On forme
On forme ![]()
donc ![]()
et ![]() .
.
![]() On forme
On forme ![]()
![]()
![]()
et ![]() .
.
La droite d’équation ![]() est asymp- tote oblique à la courbe.
est asymp- tote oblique à la courbe.
![]() Position par rapport à l’asymptote
Position par rapport à l’asymptote
![]() est du signe de
est du signe de ![]()
La courbe est au dessus de l’asymptote sur ![]() et en dessous sur
et en dessous sur ![]() .
.
Question 2 :
![]() est dérivable sur
est dérivable sur ![]() .
.
![]()
![]()
![]() .
.
![]() est racine évidente de
est racine évidente de ![]()
l’autre racine est égale au produit des racines donc égale à ![]() , ce qui permet la factorisation
, ce qui permet la factorisation
![]()
![]() est du signe de
est du signe de ![]() .
.
![]() est strictement croissante sur
est strictement croissante sur ![]() et sur
et sur ![]()
et strictement décroissante sur ![]() et sur
et sur ![]() .
.
Question 3 :
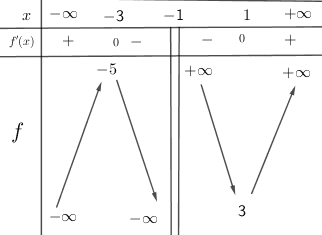
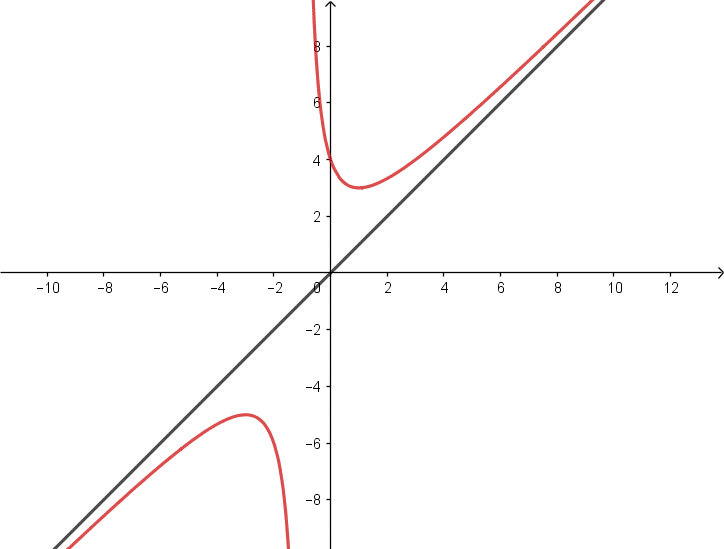
Découvrez encore plus d’exercices de maths en Terminale et de corrigés d’exercices sur notre application mobile PrepApp. Visez également la mention très bien au bac, en prenant des cours particuliers en maths pour compléter vos révisions personnelles avec les cours en ligne de maths en terminale, comme par exemple :

