Chapitres Maths en Terminale Générale

Exercices et corrigés : raisonnement par récurrence en Terminale

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.9 (1049 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Terminale

Testez-vous et vérifiez vos connaissances sur le chapitre du raisonnement par récurrence au programme de spécialité maths en Terminale avec les exercices avec corrigés détaillés proposés ci-dessous. Ce chapitre est très important et chaque année au bac, des questions sont posées sur le raisonnement par récurrence, il est donc plus que nécessaire de bien maîtriser son cours pour espérer d’excellents résultats au bac surtout avec le fort le coefficient au bac de l’épreuve de maths. N’hésitez pas à consulter les annales de maths du bac pour le constater. Si vous ne parvenez pas à résoudre ces exercices avec la rédaction adéquate, n’hésitez pas à consulter le résumé de cours sur la récurrence en terminale.

1. Exercices de récurrence sur le terme général d’une suite

Exercice 1 : Récurrence et terme général d’une suite numérique :

Soit la suite numérique définie par $u_0 = 2$ et si $n \in\mathbb{N}$ , $u_{n + 1}= u_n + 2\, n + 5$ .
Montrer que pour tout $n\in \mathbb{N}$ $\qquad \quad u_n = n ^2 + 4\, n + 2$ .

Exercice 2 sur le terme général d’une suite :

On définit la suite $(u_n)_n$ avec $u_0 = 1$ et pour tout entier $n$ , $\qquad \quad u_{n + 1} = \displaystyle \frac {1 } 3 \, u_n + n - 2$ .
Montrer que pour tout entier $n$ , $\qquad u_n = \displaystyle \frac {25} 4 . \frac {1} {3 ^n} + \frac {3\, n } 2 - \frac {21} 4$ .

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

Correction de l’exercice 1 : récurrence et terme d’une suite numérique :

Si $n \in \mathbb{N}$ , on note $\qquad \quad \mathcal{P}(n) : u_n = n ^2 + 4\, n + 2$

Initialisation : Pour $n = 0$ , $n ^2 + 4\, n + 2 = 2 = u_0\,$ , $\mathcal{P}(0)$ est vraie.

Hérédité :
Soit $n \in \mathbb{N}$ fixé tel que $\mathcal{P}(n)$ soit vraie.
$u_{n + 1} = u_n + 2 \, n + 5$
$u_{n + 1} = n ^2 + 4\, n + 2 + 2\, n + 5$
$u_{n + 1} = n ^2 + 6\, n + 7$
$u_{n + 1} = (n + 1) ^2 + 4 \, n + 6$
$u_{n + 1} = (n + 1)^2 + 4\, (n + 1) + 2$
donc $\mathcal{P}(n + 1)$ est vraie.

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$ .

Correction de l’exercice 2 sur le terme d’une suite :

Si $n \in \mathbb{N}$ , on note $\mathcal{P}(n)$ : $\qquad u_n = \displaystyle \frac {25} 4 . \frac {1} {3 ^n} + \frac {3\, n } 4 - \frac {21} 4$ .

Initialisation : Pour $n = 0$ , $\displaystyle \frac {25} 4 . \frac {1} {3 ^n} - \frac {3\, n } 4 - \frac {21} 4 = \displaystyle \frac {25} 4 . \frac {1} {1} - \frac {0} 4 - \frac {21} 4$
$\qquad =\displaystyle \frac {25 - 21} 4 = 1 = u_0$
Donc $\mathcal{P}(0)$ est vraie.

Hérédité : Soit $n \in \mathbb{N}$ donné tel que $\mathcal {P}(n)$ soit vraie.
$u_{n + 1} = \displaystyle \frac {1 } 3 \, u_n + n - 2$
$\; \; = \displaystyle \frac 1 3 \left ( \frac {25} 4 . \frac {1} {3 ^n} + \frac {3\, n } 2 - \frac {21} 4 \right ) + n - 2$
$u_{n + 1} = \displaystyle \frac {25} 4 . \frac {1} {3 ^{n + 1} } + \frac {n } 2 - \frac {7} 4 + n - 2$
$u_{n + 1} = \displaystyle \frac {25} 4 . \frac {1} {3 ^{n + 1} } + \frac {3\, n } 2 - \frac {15} 4$

On calcule d’autre part :
$\displaystyle \frac {25} 4 . \frac {1} {3 ^{n + 1} } + \frac {3\, (n + 1) } 2 - \frac {21} 4$
$\quad \displaystyle = \frac {25} 4 . \frac {1} {3 ^{n + 1} } + \frac {3\, n } 2 + \frac 3 2 - \frac {21} 4$
$\quad =\displaystyle \frac {25} 4 . \frac {1} {3 ^{n + 1} } + \frac {3\, n } 2 + - \frac {15} 4$
et on a donc prouvé que $u_{n + 1} = \displaystyle \frac {25} 4 . \frac {1} {3 ^{n + 1} } + \frac {3\, (n + 1) } 2 - \frac {21} 4$

On a démontré que $\mathcal {P}(n + 1)$ est vraie.

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$ .

Pour démontrer une égalité de la forme $A = B$ , il est plus élégant de partir de $A$ pour arriver à $B$ .
Lorsque cela vous paraît trop compliqué, vous pouvez comme ici, démontrer que $A$ et $B$ sont égales à la même quantité $C$ .
Ce sera peut être ce que vous ferez pour démontrer passer de $\mathcal{P}(n)$ à $\mathcal{P}(n + 1)$ , en écrivant l’égalité que vous devez prouver au rang $n + 1$ en la simplifiant.

2. Somme de termes d’une suite et exercices de récurrence en terminale

Exercice 1 sur la somme de termes et récurrence :

Pour tout entier $n\in \mathbb{N}^*$ , on note
$S_n$ $= \displaystyle \frac 2 {1(1+1)(1+2) }+ \frac 2 {2.(2 + 1) (2 + 2)}$ $\qquad \qquad \displaystyle + \cdots + \frac 2 {n(n + 1)(n + 2)}$
Pour tout $n \in \mathbb{N }^*$ , montrer que $\qquad S_n = \displaystyle \frac {n(n + 3)} {2(n + 1) (n + 2)}$

Exercice 2 sur la somme de termes en terminale :

On note 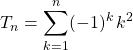$T_n = \displaystyle \sum _ {k = 1} ^n (-1) ^k \, k ^2$
$= (-1) ^1 . 1^2 + (-1) ^2 . 2^2 + \cdots + (-1) ^n \, n ^2$
et 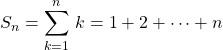$S_n = \displaystyle \sum _ {k = 1} ^n \, k = 1 + 2 + \cdots + n$ .
Montrer que pour tout $n \in \mathbb{N}^*$ , $\qquad \qquad \qquad T_n = (-1 ) ^{n} \, S_n\,$ .

Correction de l’exercice 1 sur la somme de termes et récurrence :

On note pour $n \in \mathbb{N}^* ,$ $\qquad \mathcal{P}(n) : S_n = \displaystyle \frac {n(n + 3)} {2(n + 1) (n + 2)}$

Initialisation : Si $n = 1,$
$\displaystyle \frac {n(n + 3)} {2(n + 1) (n + 2)}= \frac {1 . 4}{2 . 2 . 3} = \frac 1 3$
$\displaystyle \qquad \quad = \frac 2 {1 . (1 + 1) (1 + 2) }$
donc $\mathcal{P}(1)$ est vraie.

Hérédité : Soit $n \in \mathbb{N}^*$ fixé tel que $\mathcal{P}(n)$ soit vraie.
Alors $S_{n + 1} = \displaystyle S_n + \frac {2} {(n + 1)(n + 2)(n + 3)}$
donc par $\mathcal{P}(n)$ ,
$S_{n + 1} = \displaystyle \frac {n(n + 3)} {2(n + 1) (n + 2)}$ $\qquad \qquad \qquad \displaystyle +\, \frac {2} {(n + 1)(n + 2)(n + 3)}$
$S_{n + 1} = \displaystyle \frac {n(n + 3) ^2 + 4 } {2(n + 1)(n + 2)(n + 3)}$

On transforme
$A(n) = n(n + 3)^2 + 4$
$A(n) = n(n ^2 + 6\, n + 9) + 4$
$A(n) = n ^3 + 6\, n^2 + 9\, n + 4$
Sachant que l’on doit obtenir $S_{n + 1} = \displaystyle \frac {(n + 1)(n + 4)} {2(n + 2)(n + 3 )}$
On calcule $(n + 1) ^2\, (n + 4) = (n ^2 + 2\, n + 1) (n + 4)$ $\qquad = n ^3 + 6 \, n^2 + 9\, n + 4$
alors
$S(n + 1) = \displaystyle \frac {(n + 1)^2(n + 4)} {2(n + 1)(n + 2)(n + 3)}$
ce qui donne après simplification $S_{n + 1} = \displaystyle \frac {(n + 1)(n +4)} {2(n + 2)(n + 3)}$ .
On a établi que $\mathcal{P}(n + 1)$ est vraie.

Conclusion : par récurrence, la propriété est vraie pour tout entier $n \in \mathbb{N}^*$ .

Correction de l’exercice 2 sur la somme de terme en Terminale :

Si $n\in \mathbb{N}^*$ , $\mathcal {P}(n)$ : $T_n = (-1 ) ^{n} \, S_n$ .

Initialisation :
$T_1 = (-1) ^2 . 1 ^2 = (-1) ^1 \, S_1$ donc $\mathcal {P}(1)$ est vraie.

Hérédité :
Soit $n \in \mathbb{N}^*$ donné tel que $\mathcal {P}(n)$ soit vraie.
$T_{n + 1} = T_n + (-1) ^{n + 1} \, (n + 1) ^2$ $T_{n + 1} = (-1)^n S_n + (-1) ^{n + 1} \, (n + 1) ^2$
donc $T_{n + 1} = (-1)^{n + 1} \left ( (n + 1) ^2 - S_{n} \right )$

Pour un résultat classique :
$T_{n + 1} = \displaystyle (-1)^{n + 1} \left ( (n + 1) ^2 - \frac {n ( n +1)} 2 \right )$
$T_{n + 1} = \displaystyle (-1)^{n + 1} \frac {n + 1} 2 \left ( 2 (n + 1) - n \right )$
$T_{n + 1} = \displaystyle (-1)^{n + 1} \frac {n + 1} 2 ( n + 2 )$
$T_{n + 1} = \displaystyle (-1)^{n + 1} \, S_{n + 1}$
donc on a prouvé $\mathcal {P}(n + 1)$ .

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$ au moins égal à 1.

3. Inégalités et récurrence en terminale générale

Exercice 1 sur les inégalités dans le raisonnement par récurrence :

On définit la suite $(u_n)_n$ avec $u_0 = 1$ et pour tout entier $n$ , $u_{n + 1} = \displaystyle \frac {9 } {6 - u_n}$
Ces relations définissent une suite telle que pour tout entier $0 < u_n < 3$

Exercice 2 sur les inégalités dans le raisonnement par récurrence :

On définit la suite $(u_n)_n$ avec $u_0 = 2$ et pour tout entier $n$ , $u_{n + 1} = \displaystyle \frac {2\, u_n + 1 } {u_n + 1 }$
Ces relations définissent une suite telle que pour tout entier $3/2 < u_n \leqslant 2$ .

Correction de l’exercice 1 sur les inégalités, la récurrence en Terminale :

Si $n \in \mathbb{N}$ , on note $\mathcal{P}(n)$ : $u_n$ est défini et $0 < u_n < 3$ .

Initialisation : Par hypothèse, $u_0$ est défini et vérifie $0 < u_0 < 3$ donc $\mathcal{P}(0)$ est défini.

Hérédité : Soit $n \in \mathbb{N}$ donné tel que $\mathcal {P}(n)$ soit vraie.
On peut alors définir $u_{n + 1}$ car $6 -u_n \neq 0$
$\ast$ Comme $u_n > 0$ et $6 - u_n > 0$ , par quotient $u_{ n+ 1} > 0$ .

$\ast$ $3 - u_{n + 1} = 3 - \displaystyle \frac 9 {6 - u_n}$
$3 - u_{n + 1} = \displaystyle \frac {3(6 - u_n - 3)} {6 - u_n}$
$3 - u_{n + 1} = \displaystyle \frac {3(3 - u_n) } {6 - u_n} > 0$ .
On a démontré $\mathcal {P}(n + 1)$ .

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$ .

Correction de l’exercice 2 sur les inégalités, la récurrence en Terminale :

Si $n \in \mathbb{N}$ , on note
$\;\; \mathcal{P}(n)$ : $u_n$ est défini et $3/2 < u_n \leqslant 2$ .

Initialisation : Par hypothèse, $u_0$ est défini et vérifie $3/2 < u_0 \leqslant 2$ donc $\mathcal{P}(0)$ est vraie.

Hérédité : Soit $n \in \mathbb{N}$ donné tel que $\mathcal {P}(n)$ soit vraie.
On peut alors définir $u_{n + 1}$ car $1 \leqslant u_n \leqslant 2 \Rightarrow u_n + 1 > 0$ .

$\ast$ $u_{n + 1} - \displaystyle \frac 3 2 = \displaystyle \frac {2\, u_n + 1 } {u_n + 1 } - \frac 3 2$
$u_{n + 1} - \displaystyle \frac 3 2 = \displaystyle \frac { 4\, u _n + 2 - 3\, u_n - 3 } {2(u_n + 1 )}$
$u_{n + 1} - \displaystyle \frac 3 2 = \displaystyle \frac { u _n - 1 } {2(u_n + 1 )} > 0$

$\ast$ $\displaystyle 2 - u_{n + 1} = \displaystyle 2 - \frac {2\, u_n + 1 } {u_n + 1 }$
$2 - u_{n + 1} = \displaystyle \frac { 1 } {u_n + 1 } > 0$
On a démontré $\mathcal {P}(n + 1)$ .

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

4. Exercices confondus sur le raisonnement par récurrence en Terminale

Exercice 1 le raisonnement par récurrence en Terminale :

On dit qu’un entier $n$ est divisible par $9$ lorsqu’il existe $k\in \mathbb{Z}$ tel que $n = 9\, k$ .
Montrer que pour tout entier $n$ non nul, $9$ divise $4 ^n + 15\, n - 1$ . Cet exercice est classique en arithmétique.

Exercice 2 le raisonnement par récurrence en Terminale :

On dit que 6 divise $N \in \mathbb{N}$ lorsqu’il existe $k \in \mathbb{N}$ et que $N = 6\, k$ .
Montrer que pour tout entier $n$ , 6 divise $5 \, n ^3 + n$

Correction de l’exercice 1 sur le raisonnement par récurrence en Terminale :

Si $n\in \mathbb{N}^*$ , on note
$\qquad \quad \mathcal{P}(n)$ : $9$ divise $4 ^n + 15\, n - 1$

Initialisation : pour $n = 1$ $4 ^n + 15 \, n - 1 = 4 + 15 - 1 = 18 = 9 \times 2$ donc $\mathcal{P}(1)$ est vraie.

Hérédité : On suppose que $\mathcal{P}(n)$ est vraie pour un entier $n \in \mathbb{N}^*$ donné.
Soit en notant $u_n = 4 ^n + 15\, n - 1$ , il existe $k\in \mathbb{Z}$ tel que $u_n = 9\, k$ .
$u_{n + 1} = 4 ^{n + 1} + 15\, n + 15 - 1$ $u_{n + 1 } = 4 (4 ^n + 15\, n - 1)$ $\qquad \qquad \qquad +\, (15 - 60)\, n + 14 + 4$
On reconnaît $u_n$ et on utilise $\mathcal[P}(n)$ :
$u_{n + 1} = 4 (9\, k ) - 45 \, n + 18$
$u_{n + 1} = 9 (4\, k - 5 \, n + 2)$
comme $4\, k - 5\, n + 2 \in \mathbb{Z}$ , alors $9$ divise $u_{n + 1}$ .
On a prouvé $\mathcal {P}(n + 1)$ .

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$

Correction de l’exercice 2 sur le raisonnement par récurrence en Terminale :

Si $n \in \mathbb{N}$ , on note $\mathcal{P}(n)$ : 6 divise $5 \, n ^3 + n$ c.a.d. on peut trouver $k \in \mathbb{N}$ tel que $5\, n ^3 + n = 6 \, k$

Initialisation : Par hypothèse, $0^3 + 0 = 6 . 0$ donc $\mathcal{P}(0)$ est vraie.

Hérédité : Soit $n \in \mathbb{N}$ donné tel que $\mathcal {P}(n)$ soit vraie.
Il existe $k \in \mathbb{N}$ tel que $5 \, n ^3 + n = 6 \, k$
On note $u_n = 5\, n ^3 + n$ et $u_{n + 1} = 5\, (n + 1) ^3 + (n + 1)$
$u_{n + 1} = 5(n ^3 + 3 \, n ^2 + 3\, n + 1) + n + 1$
$u_{n + 1} = 5 \, n ^3 + n + (15 \, n ^2 + 15 \, n) + 6$
$u_{n + 1} = 6 . k + 15 \, n(n + 1) + 6$
$n(n + 1)$ est le produit de deux entiers consécutifs, l’un est pair et l’autre impair, il est pair donc il peut s’écrire $n(n + 1) = 2 \, p$ avec $p \in \mathbb{N}$
$u_{n + 1} = 6 . k + 15 \, ( 2 \,p )+ 6$ $u_{n + 1}= 6\, (k + 5 \, p + 1)$
donc 6 divise $u_{n + 1}$ .
On a prouvé que $\mathcal{P}(n + 1)$ est vraie.

Conclusion : par récurrence, la propriété est vraie pour tout entier $n$

Ces exercices sont un avant goût. Vous trouverez beaucoup plus d’exercices et d’annales corrigées dans notre application mobile. N’hésitez pas à faire appel à un professeur particulier pour bénéficier de cours particuliers de maths et progresser encore plus, ou consultez aussi les nombreux autres cours en ligne de maths en terminale, comme les chapitres suivants :

Exercices et corrigés : raisonnement par récurrence en Terminale

1. Exercices de récurrence sur le terme général d’une suite

Exercice 1 : Récurrence et terme général d’une suite numérique :

Exercice 2 sur le terme général d’une suite :

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Correction de l’exercice 1 : récurrence et terme d’une suite numérique :

Correction de l’exercice 2 sur le terme d’une suite :

2. Somme de termes d’une suite et exercices de récurrence en terminale

Exercice 1 sur la somme de termes et récurrence :

Exercice 2 sur la somme de termes en terminale :

Correction de l’exercice 1 sur la somme de termes et récurrence :

Correction de l’exercice 2 sur la somme de terme en Terminale :

3. Inégalités et récurrence en terminale générale

Exercice 1 sur les inégalités dans le raisonnement par récurrence :

Exercice 2 sur les inégalités dans le raisonnement par récurrence :

Correction de l’exercice 1 sur les inégalités, la récurrence en Terminale :

Correction de l’exercice 2 sur les inégalités, la récurrence en Terminale :

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

4. Exercices confondus sur le raisonnement par récurrence en Terminale

Exercice 1 le raisonnement par récurrence en Terminale :

Exercice 2 le raisonnement par récurrence en Terminale :

Correction de l’exercice 1 sur le raisonnement par récurrence en Terminale :

Correction de l’exercice 2 sur le raisonnement par récurrence en Terminale :

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales