Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Analyse Asymptotique en Maths Sup MPSI, MP2I, PCSI, PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Maths Sup Analyse Asymptotique
Résultats et Application directe du cours
Plan :
1. Suites dominées et négligeables
2. Suites équivalentes
3. Fonctions dominées et négligeables
4. Fonctions équivalentes
5. Équivalents usuels
6. Opérations autorisées sur les équivalents
7. Opérations interdites sur les équivalents
8. Des méthodes pour obtenir des équivalents
9. D’autres fautes à éviter
10. Équivalents en ![]()
11. Équivalents en ![]()
12. Équivalents en ![]()
13. Deux équivalents de suites
14. Fonctions dominées, négligeables et équivalentes
15. Suites dominées, négligeables et équivalentes
Remarque : certains points supposent que les DL ont été vus, ne pas en tenir compte si ce n’est pas le cas.
1. Suites dominées et négligeables
1.1. Suites dominées
Soient ![]() et
et ![]() deux suites réelles ou complexes.
deux suites réelles ou complexes.
![]() On dit que la suite
On dit que la suite ![]() est dominée par la suite
est dominée par la suite ![]() et on écrit
et on écrit ![]() ou
ou ![]()
(on lit : ![]() est un grand O de
est un grand O de ![]() ) si, et seulement si,
) si, et seulement si,
![]()
![]() .
.
![]() S’il existe un entier
S’il existe un entier ![]() tel que si
tel que si ![]() , la suite
, la suite ![]() est dominée par la suite
est dominée par la suite ![]() ssi la suite
ssi la suite ![]() est bornée.
est bornée.
![]()
![]() ssi la suite
ssi la suite ![]() est bornée.
est bornée.
![]() Si
Si ![]() et
et ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]() .
.
![]() Puissance : si
Puissance : si ![]() ,
,
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() , si
, si ![]() ,
, ![]()
![]() si
si ![]() et
et ![]() , si
, si ![]() ,
, ![]() .
.
1.2. Suites négligeables
Soient ![]() et
et ![]() deux suites réelles ou complexes,
deux suites réelles ou complexes,
![]() On dit que la suite
On dit que la suite ![]() est négligeable devant la suite
est négligeable devant la suite ![]() et on écrit
et on écrit ![]() ou
ou ![]() (on lit :
(on lit : ![]() est un petit o de
est un petit o de ![]() ) si, et seulement si,
) si, et seulement si, ![]()
![]() .
.
si, et seulement si, il existe une suite ![]() de limite nulle telle que
de limite nulle telle que ![]() .
.
![]() S’il existe un entier
S’il existe un entier ![]() tel que si
tel que si ![]() , la suite
, la suite ![]() est négligeable devant la suite
est négligeable devant la suite ![]() ssi la suite
ssi la suite ![]() converge vers 0.
converge vers 0.
![]()
![]() ssi la suite
ssi la suite ![]() converge vers 0.
converge vers 0.
![]() Soient
Soient ![]() et
et ![]() deux suites réelles ou complexes telles que
deux suites réelles ou complexes telles que ![]() , alors
, alors ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]() .
.
![]() Puissance : si
Puissance : si ![]() ,
,
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() , si
, si ![]() ,
, ![]()
![]()
![]() et
et ![]() ,
, ![]() ,
, ![]() .
.
1.3. Traduction des résultats sur les croissances comparées
Comparaison des suites de référence :
![]()
![]() si
si ![]() et
et ![]() .
.
![]()
![]() si
si ![]() et
et ![]()
![]()
![]() pour tout
pour tout ![]() .
.
![]()
![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
2. Suites équivalentes
2.1. Définitions
Soient ![]() et
et ![]() deux suites réelles ou complexes.
deux suites réelles ou complexes.
![]() Il y a équivalence entre :
Il y a équivalence entre :
![]() il existe une suite
il existe une suite ![]() qui converge vers
qui converge vers ![]() telle que
telle que ![]()
![]() il existe une suite
il existe une suite ![]() qui converge vers
qui converge vers ![]() telle que
telle que ![]()
![]()
![]() .
.
On dit alors que les suites ![]() et
et ![]() sont équivalentes et on écrit :
sont équivalentes et on écrit : ![]() ou
ou ![]() .
.
![]() S’il existe un entier
S’il existe un entier ![]() tel que si
tel que si ![]() , la suite
, la suite ![]() est équivalente à la suite
est équivalente à la suite ![]() ssi la suite
ssi la suite ![]() converge vers 1.
converge vers 1.
![]() La relation « les suites sont équivalentes » est une relation d’équivalence sur l’ensemble des suites réelles (resp. complexes) :
La relation « les suites sont équivalentes » est une relation d’équivalence sur l’ensemble des suites réelles (resp. complexes) :
![]()
![]() ssi
ssi ![]() .
.
![]()
![]() et
et ![]()
![]() .
.
2.2. Opérations sur les suites équivalentes
Les suites introduites sont réelles ou complexes.
![]() Si
Si ![]() ,
, ![]() .
.
![]() si
si ![]() et
et ![]()
![]()
![]()
![]() si à partir d’un certain rang
si à partir d’un certain rang ![]() ,
, ![]() .
.
![]() Puissance et équivalents
Puissance et équivalents
![]() si
si ![]() ,
, ![]()
![]()
![]() si
si ![]() et si
et si ![]() pour
pour ![]() ,
, ![]()
![]() si
si ![]() et si
et si ![]() et
et ![]() pour
pour ![]() ,
,
![]()
![]() .
.
⚠️ il est indispensable de retenir qu’aucun résultat ne permet de faire une somme ou une différence d’équivalents donc qu’il sera nécessaire d’effectuer un raisonnement complet dans le cas d’une somme ou d’une différence.
De même, il est impossible de dire que si ![]() ,
, ![]() , propriété qui est fausse en général.
, propriété qui est fausse en général.
2.3. Suites équivalentes et limites
![]() Soient
Soient ![]() et
et ![]() deux suites équivalentes.
deux suites équivalentes.
![]() Si ce sont des suites de réels non nuls,
Si ce sont des suites de réels non nuls, ![]() et
et ![]() sont de même signe pour
sont de même signe pour ![]() assez grand.
assez grand.
![]() si
si ![]() (
(![]() fini ou
fini ou ![]() ), alors
), alors ![]() .
.
![]() Si la suite
Si la suite ![]() converge vers le complexe non nul
converge vers le complexe non nul ![]() ,
, ![]() .
.
⚠️ Si la suite n’est pas la suite nulle, on ne doit jamais obtenir ![]() .
.
2.4. Formule de Stirling
![]() .
.
3. Fonctions dominées et négligeables
3.1. Fonctions dominées
Soient ![]() et
et ![]() deux fonctions définies dans un voisinage
deux fonctions définies dans un voisinage ![]() de
de ![]() (sauf peut-être en
(sauf peut-être en ![]() ) réelles ou complexes.
) réelles ou complexes.
![]() On dit que la fonction
On dit que la fonction ![]() est dominée par la fonction
est dominée par la fonction ![]() lorsque
lorsque ![]() et on écrit
et on écrit ![]() (on lit :
(on lit : ![]() est un grand O de
est un grand O de ![]() si
si ![]() ) s’il existe un voisinage
) s’il existe un voisinage ![]() de
de ![]() inclus dans
inclus dans ![]() et un réel
et un réel ![]() tel que
tel que
![]() ,
, ![]() .
.
![]() S’il existe un voisinage
S’il existe un voisinage ![]() de
de ![]() sur lequel
sur lequel ![]() est non nulle (sauf peut être en
est non nulle (sauf peut être en ![]() ), la fonction
), la fonction ![]() est dominée par la fonction
est dominée par la fonction ![]() lorsque la fonction
lorsque la fonction ![]() est bornée au voisinage de
est bornée au voisinage de ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]() .
.
![]() Puissance : Si
Puissance : Si ![]() ,
,
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() et si
et si ![]() au voisinage de
au voisinage de ![]() ,
, ![]()
![]() si
si ![]() , si
, si ![]() et
et ![]() sont à valeurs strictement positives au voisinage de
sont à valeurs strictement positives au voisinage de ![]() ,
, ![]() .
.
3.2. Fonctions négligeables
Soient ![]() et
et ![]() deux fonctions définies dans un voisinage
deux fonctions définies dans un voisinage ![]() de
de ![]() (sauf peut-être en
(sauf peut-être en ![]() ) réelles ou complexes
) réelles ou complexes
![]() On dit que la fonction
On dit que la fonction ![]() est négligeable devant la fonction
est négligeable devant la fonction ![]() lorsque
lorsque ![]() ) et on écrit
) et on écrit
![]()
(on lit : ![]() est un petit o de
est un petit o de ![]() si
si ![]() ) si pour tout
) si pour tout ![]() , il existe un voisinage
, il existe un voisinage ![]() de
de ![]() inclus dans
inclus dans ![]() tel que
tel que ![]()
ssi il existe une fonction ![]() définie au voisinage de
définie au voisinage de ![]() et de limite nulle en
et de limite nulle en ![]() telle que
telle que ![]() .
.
![]() S’il existe un voisinage
S’il existe un voisinage ![]() de
de ![]() sur lequel
sur lequel ![]() est non nulle (sauf peut être en
est non nulle (sauf peut être en ![]() ), la fonction
), la fonction ![]() est négligeable devant la fonction
est négligeable devant la fonction ![]() ssi la fonction
ssi la fonction ![]() est tend vers
est tend vers ![]() en
en ![]() .
.
exemple : Si ![]() ,
,
![]()
![]()
![]()
![]() .
.
![]() Soient
Soient ![]() et
et ![]() deux fonctions définies dans un voisinage
deux fonctions définies dans un voisinage ![]() de
de ![]() ,
,
![]() .
.
![]() Si
Si ![]() et
et ![]() ,
, ![]() .
.
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]() .
.
![]() Puissance : si
Puissance : si ![]()
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() et si
et si ![]() au voisinage de
au voisinage de ![]() ,
, ![]()
![]() si
si ![]() et
et ![]() sont à valeurs strictement positives au voisinage de
sont à valeurs strictement positives au voisinage de ![]() et si
et si ![]() ,
, ![]() .
.
3.3. Traduction des résultats sur les croissances comparées
![]() Si
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
4. Définition de fonctions équivalentes
Soient ![]() et
et ![]() deux fonctions réelles ou complexes définies dans un voisinage
deux fonctions réelles ou complexes définies dans un voisinage ![]() de
de ![]() (sauf peut-être en
(sauf peut-être en ![]() ).
).
![]() Il y a équivalence entre :
Il y a équivalence entre :
![]() il existe une fonction
il existe une fonction ![]() définie dans
définie dans ![]() de limite nulle en
de limite nulle en ![]() telle que
telle que ![]()
![]() il existe une fonction
il existe une fonction ![]() définie dans
définie dans ![]() de limite égale à
de limite égale à ![]() en
en ![]() telle que
telle que ![]()
![]()
![]() .
.
On dit que ![]() et
et ![]() sont équivalentes en
sont équivalentes en ![]() et on écrit
et on écrit ![]() .
.
![]() S’il existe un voisinage de
S’il existe un voisinage de ![]() sur lequel
sur lequel ![]() (sauf peut être en
(sauf peut être en ![]() ), la fonction
), la fonction ![]() est équivalente à la fonction
est équivalente à la fonction ![]() en
en ![]() ssi la fonction
ssi la fonction ![]() admet
admet ![]() pour limite en
pour limite en ![]() .
.
![]() La relation « les fonctions sont équivalentes en
La relation « les fonctions sont équivalentes en ![]() » est une relation d’équivalence sur l’ensemble des fonctions réelles (resp. complexes) définies au voisinage de
» est une relation d’équivalence sur l’ensemble des fonctions réelles (resp. complexes) définies au voisinage de ![]() .
.
![]()
![]() ssi
ssi ![]()
![]()
![]() et
et ![]()
![]() .
.
5. Équivalents usuels
![]() équivalents en 0 :
équivalents en 0 :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
👍 Tous ces équivalents (sauf 2 justifiés ci dessous) peuvent être retrouvés à l’aide des taux d’accroissement en ![]() et de la dérivée en
et de la dérivée en ![]() .
.
Lorsque vous aurez étudié les développements limités, vous pourrez les retrouver en prenant le premier terme non nul du développement limité de la fonction considérée en 0.
Pour voir la démonstration de
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
et en utilisant ![]() ,
,
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
et en utilisant ![]() ,
,
![]() .
.
![]() équivalents en 1 :
équivalents en 1 :
![]()
![]()
![]()
![]()
Démo : ![]() On écrit
On écrit ![]() et on utilise
et on utilise ![]() avec
avec ![]() .
.
![]() Si
Si ![]() tend vers
tend vers ![]() ,
, ![]() tend vers 0 et comme
tend vers 0 et comme ![]() , alors
, alors ![]()
puis on utilise ![]()
On démontre ce résultat en écrivant que ![]()
![]()
On termine en utilisant ![]() car
car ![]()
![]() équivalents en
équivalents en ![]() :
:
![]()
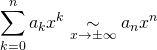 si
si ![]()
![]()
![]()
![]()
![]() .
.
Démo : On écrit ![]()
et ![]()
avec ![]() .
.
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
6. Opérations autorisées sur les équivalents
Produit :
![]() et
et ![]()
![]()
![]()
Quotient :
![]() et
et ![]() et
et ![]()
![]()
![]()
Passage à la valeur absolue :
![]()
![]()
![]()
Puissance :
![]()
![]()
![]()
(en imposant si ![]()
![]() et
et ![]() à valeurs strictement positives).
à valeurs strictement positives).
Composition à droite :
![]() et si
et si ![]() ,
, ![]()
⚠️ La composition à gauche est fausse en général, c’est-à-dire si
![]() , on ne peut pas dire en dehors de la valeur absolue ou de la fonction puissance
, on ne peut pas dire en dehors de la valeur absolue ou de la fonction puissance ![]() que
que ![]() .
.
7. Opérations interdites sur les équivalents
👍 Une vérification qui peut aider à corriger des fautes : si la fonction ou la suite n’est pas nullle, on ne peut pas trouver un équivalent égal à 0.
Addition :
![]() ,
, ![]() et
et ![]() et n’est pas équivalent à 0.
et n’est pas équivalent à 0.
Différence :
![]() ,
, ![]() et
et ![]() et n’est pas équivalent à 0.
et n’est pas équivalent à 0.
Passage au logarithme pour des fonctions admettant 1 pour limite :
![]() et
et ![]() n’impliquent pas que
n’impliquent pas que ![]() .
.
Exemple :
![]() et
et ![]() alors que
alors que ![]() donc
donc ![]() et
et ![]() ne sont pas équivalents en 0.
ne sont pas équivalents en 0.
Passage à l’exponentielle :
![]() et
et ![]() n’impliquent pas que
n’impliquent pas que ![]() .
.
Exemple :
![]() est équivalent à
est équivalent à ![]() en
en ![]() mais
mais ![]() n’est pas équivalent à
n’est pas équivalent à ![]() car le quotient
car le quotient ![]() ne tend pas vers 1.
ne tend pas vers 1.
Passage à la puissance :
![]()
![]() n’implique pas
n’implique pas ![]() et n’implique pas que
et n’implique pas que ![]() lorsque
lorsque ![]() n’est pas une constante.
n’est pas une constante.
![]() De même,
De même, ![]() n’implique pas
n’implique pas ![]() .
.
Voir les exemples justifiant les interdictions pour le passage à la puissance
Exemple 1 :
![]()
![]() est équivalent à
est équivalent à ![]() en
en ![]() , mais
, mais ![]() n’est pas équivalent à
n’est pas équivalent à ![]() car le quotient
car le quotient ![]() tend vers
tend vers ![]() .
.
![]() De même
De même ![]() n’est pas équivalent à
n’est pas équivalent à ![]() en
en ![]() car le quotient
car le quotient ![]() tend vers e en
tend vers e en ![]() .
.
Exemple 2 :
Soit ![]() et
et ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
, ![]() et
et ![]() ne sont pas équivalents.
ne sont pas équivalents.
8. Des méthodes pour obtenir des équivalents
![]() M1. Utilisation de la limite
M1. Utilisation de la limite
Si ![]() admet une limite finie non nulle
admet une limite finie non nulle ![]() en
en ![]() ,
, ![]() .
.
![]() M2. Utilisation de la dérivée.
M2. Utilisation de la dérivée.
Si ![]() est dérivable en
est dérivable en ![]() et si
et si ![]() est non nul,
est non nul, ![]() .
.
Exemple :
![]()
![]() M3. Si
M3. Si ![]() et
et ![]() sont des fonctions à valeurs dans
sont des fonctions à valeurs dans ![]() , de limite nulle en
, de limite nulle en ![]() vérifiant
vérifiant ![]() , pour démontrer que
, pour démontrer que ![]() ,
,
on écrit ![]() avec
avec ![]() .
.
Démonstration : On écrit ![]() avec
avec ![]() .
.
Les fonctions utilisées étant à valeurs strictement positives, on peut écrire
![]()
Comme ![]() , au voisinage de
, au voisinage de ![]() ,
, ![]() donc
donc
![]() avec
avec ![]() donc
donc ![]()
Cas particulier : ![]() .
.
Démonstration : ![]() ,
, ![]() avec
avec ![]() .
.
![]() M4. Si
M4. Si ![]() et
et ![]() sont des fonctions à valeurs dans
sont des fonctions à valeurs dans ![]() , de limite égale à
, de limite égale à ![]() en
en ![]() vérifiant
vérifiant ![]() , pour démontrer que :
, pour démontrer que : ![]() ,
,
on écrit ![]() avec
avec ![]()
Démo : Les fonctions utilisées étant à valeurs strictement positives, on peut écrire ![]()
Comme ![]() , au voisinage de
, au voisinage de ![]() ,
, ![]() donc
donc ![]() avec
avec ![]() donc
donc ![]() .
.
Cas particulier : ![]() .
.
Démo : ![]() ,
, 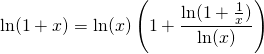 avec
avec ![]() .
.
On a prouvé que :
![]() .
.![]() ,
, 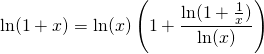 avec
avec ![]() .
.
On a prouvé que :
![]() .
.
![]() M5. Par utilisation de la propriété
M5. Par utilisation de la propriété ![]() et
et ![]() , alors
, alors ![]() .
.
conséquence :
Si ![]() où
où ![]() et
et ![]() ,
, ![]() , par utilisation de la propriété précédente car
, par utilisation de la propriété précédente car ![]()
Exemple :
![]()
Si 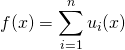 , l’une au moins des fonctions tendant vers
, l’une au moins des fonctions tendant vers ![]() , on met en facteur la fonction qui tend le plus vite vers l’infini.
, on met en facteur la fonction qui tend le plus vite vers l’infini.
Exemple : équivalent en ![]() de
de
![]() .
.
Correction :
![]()
![]() où la fonction
où la fonction ![]() admet 0 pour limite en
admet 0 pour limite en ![]() , donc
, donc ![]() .
.
👍 Si l’on ne devine pas quelle est la fonction qui tend le plus vite vers l’infini, dans un cas comme celui-ci, il n’y aurait au maximum que trois factorisations à essayer !
![]() M7. Cas d’une somme de fonctions, chacune des fonctions admettant 0 pour limite.
M7. Cas d’une somme de fonctions, chacune des fonctions admettant 0 pour limite.
Si 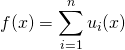 et, si pour tout
et, si pour tout ![]() , la fonction
, la fonction ![]() admet 0 pour limite en
admet 0 pour limite en ![]() , on met en facteur la fonction qui tend le moins vite vers 0.
, on met en facteur la fonction qui tend le moins vite vers 0.
Exemple : trouver un équivalent en ![]() , de
, de ![]() .
.
![]() M8. Par utilisation d’un encadrement
M8. Par utilisation d’un encadrement
Si au voisinage de ![]() ,
, ![]() ,
,
les fonctions ![]() et
et ![]() ayant même équivalent
ayant même équivalent ![]() de signe constant au voisinage de
de signe constant au voisinage de ![]() , on divise l’inégalité par
, on divise l’inégalité par ![]() et en encadrant
et en encadrant ![]() par
par ![]() et
et ![]() soit par 2 fonctions admettant 1 pour limite en
soit par 2 fonctions admettant 1 pour limite en ![]() , la fonction
, la fonction ![]() admet 1 pour limite en
admet 1 pour limite en ![]() et on en déduit que
et on en déduit que ![]() .
.
Exemple : On rappelle que ![]() représente la partie entière du réel
représente la partie entière du réel ![]() , montrer que
, montrer que ![]() .
.
![]() M9. Pour trouver un équivalent de
M9. Pour trouver un équivalent de ![]() lorsque
lorsque ![]() et
et ![]() admettent la même limite finie
admettent la même limite finie ![]() en
en ![]() .
.
On écrit ![]()
car ![]() ,
, ![]() et
et ![]()
Exemple : trouver un équivalent en ![]() de
de ![]()
![]() M10. Par utilisation d’un développement limité.
M10. Par utilisation d’un développement limité.
Si ![]() a un développement limité d’ordre
a un développement limité d’ordre ![]() au voisinage de
au voisinage de ![]() donné par
donné par ![]() ,
,
lorsqu’au moins un des coefficients ![]() est non nul,
est non nul, ![]() où
où ![]() est le plus petit entier tel que
est le plus petit entier tel que ![]()
⚠️ Important ! on ne conserve qu’un seul terme du développement limité quand on prend un équivalent, jamais une somme de plusieurs termes.
Par exemple, on écrit ![]() , on n’écrit pas que
, on n’écrit pas que ![]() est équivalent à
est équivalent à ![]()
De même, on écrit ![]() et non
et non ![]()
![]() M11. Par intégration d’un équivalent :
M11. Par intégration d’un équivalent :
si ![]() où
où ![]() ,
,
![]() .
.
9. D’autres fautes à éviter
⚠️ Lorsque ![]() , on peut dire que
, on peut dire que ![]() et
et ![]() ont même signe au voisinage de
ont même signe au voisinage de ![]() ; mais chercher un équivalent de
; mais chercher un équivalent de ![]() en
en ![]() ne peut servir à donner le signe de
ne peut servir à donner le signe de ![]() sur tout un intervalle de
sur tout un intervalle de ![]()
Exemple :
![]() donc au voisinage de 0,
donc au voisinage de 0, ![]() .
.
Si l’on veut prouver que pour tout réel ![]()
![]() on pourra, par exemple, étudier les variations de la fonction
on pourra, par exemple, étudier les variations de la fonction
![]() ,
,
calculer ![]() et en démontrant que
et en démontrant que ![]() est décroissante sur
est décroissante sur ![]() et croissante sur
et croissante sur ![]() , dire (en s’aidant éventuellement d’un tableau de variations) que pour tout réel
, dire (en s’aidant éventuellement d’un tableau de variations) que pour tout réel ![]() ,
, ![]()
⚠️ Attention à la recherche d’un équivalent à partir d’un DL, lorsque les coefficients de ce DL dépendent d’un paramètre. Certaines valeurs du paramètre peuvent annuler le terme retenu comme équivalent.
10. Équivalents en 0
Les équivalents suivants sont-ils justes ? Sinon les corriger.
1) ![]()
2) On note ![]() .
.
![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) Si ![]() et
et ![]() sont des réels distincts,
sont des réels distincts, ![]() .
.
8) ![]()
11. Équivalents au voisinage de 1
Lorsque ![]() tend vers 1, les équivalents suivants sont ils corrects ? Si oui les justifier, si non donner la bonne réponse.
tend vers 1, les équivalents suivants sont ils corrects ? Si oui les justifier, si non donner la bonne réponse.
1) ![]()
2) ![]()
3) ![]()
12. Équivalents en 
Lorsque ![]() tend vers
tend vers ![]() (ou
(ou ![]() selon le cas), les équivalents suivants sont ils corrects ?
selon le cas), les équivalents suivants sont ils corrects ?
Si oui les justifier, si non les corriger.
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
13. Deux équivalents de suites
1) ![]()
2) ![]()
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
14. Fonctions dominées, négligeables et équivalentes
Question 1
Si ![]() et
et ![]() sont définies dans un voisinage de
sont définies dans un voisinage de ![]() à valeurs dan
à valeurs dan ![]() si
si ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Question 2
Soient ![]() et
et ![]() définies au voisinage de
définies au voisinage de ![]() , on suppose que
, on suppose que
![]() et
et ![]() ,
,
alors ![]() .
.
Question 3
Soient ![]() et
et ![]() définies au voisinage de
définies au voisinage de ![]() , on suppose que
, on suppose que
![]() et
et ![]() ,
,
alors ![]() .
.
Question 4
Soient ![]() des fonctions définies dans un voisinage de
des fonctions définies dans un voisinage de ![]() .
.
On suppose que ![]() ,
, ![]() et
et ![]()
Alors ![]() .
.
Question 5
Si ![]() et
et ![]() sont définies au voisinage du réel
sont définies au voisinage du réel ![]() , équivalentes en
, équivalentes en ![]() , si
, si ![]() est dérivable en
est dérivable en ![]() ,
, ![]() l’est aussi.
l’est aussi.
Question 6
Si ![]() ,
,
![]() et
et ![]()
15. Suites dominées, négligeables et équivalentes
Dans tout le paragraphe, ![]() ,
, ![]() et
et ![]() sont des suites réelles ou complexes.
sont des suites réelles ou complexes.
Question 1
Si ![]() est bornée et
est bornée et ![]() , la suite
, la suite ![]() est bornée.
est bornée.
Question 2
Si la suite ![]() converge et si
converge et si ![]() , la suite
, la suite ![]() converge.
converge.
Question 3
Si la suite ![]() est bornée et si
est bornée et si ![]() , la suite
, la suite ![]() converge.
converge.
Question 4
Si ![]() et si
et si ![]() ,
, ![]()
Question 5
Si la suite ![]() est bornée et si
est bornée et si ![]() , la suite
, la suite ![]() converge.
converge.
Question 6
Si la suite ![]() converge vers 0 et si
converge vers 0 et si ![]() , les suites
, les suites ![]() et
et ![]() sont bornées.
sont bornées.
Question 7
Si ![]() ,
, ![]()
et plus généralement si ![]() ,
,
si ![]() ,
, ![]() .
.
Référez-vous aux autres cours en ligne de maths au programme de Maths Sup pour préparer efficacement la fin d’année. Commencez les révisions dès maintenant et assurez-vous d’obtenir de très bonnes notes à l’aide de nos cours de maths sur Paris :

