Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Arithmétique en Maths Sup en MPSI, PCSI et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Maths sup Arithmétique
Plan :
1. Divisibilité
2. PGCD de deux éléments
3. Nombres premiers entre eux
4. PPCM
5. Nombres premiers
6. Relation de congruence
7. Synthèse des méthodes
On suppose dans tout ce chapitre sauf indication contraire que ![]() ou
ou ![]() .
.
Si vous rencontrez des difficultés lors de votre entraînement sur l’arithmétique, n’hésitez pas à consulter nos profs de maths à domicile.
1. Divisibilité
1.1. Diviseurs et multiples
![]() Si
Si ![]() et
et ![]() , il y a équivalence entre :
, il y a équivalence entre :
![]()
![]() divise
divise ![]() ou
ou ![]() est un diviseur de
est un diviseur de ![]()
![]()
![]() est un multiple de
est un multiple de ![]()
![]() il existe
il existe ![]() tel que
tel que ![]() .
.
On note ![]() .
.
⚠️ Tout entier divise ![]() .
.
⚠️ ![]() ne divise que lui-même.
ne divise que lui-même.
![]() Si
Si ![]() ,
,
![]() l’ensemble des multiples de
l’ensemble des multiples de ![]() est
est ![]() .
.
![]() Il n’y a pas de notation consacrée pour les diviseurs de
Il n’y a pas de notation consacrée pour les diviseurs de ![]() .
.
J’utiliserai ![]() pour noter l’ensemble des diviseurs de
pour noter l’ensemble des diviseurs de ![]() .
.
![]()
![]()
![]() si
si ![]() et
et ![]() ,
,
![]() .
.
1.2. Propriétés
![]() la relation «
la relation « ![]() » est une relation d’ordre sur
» est une relation d’ordre sur ![]() mais n’est pas une relation d’ordre sur
mais n’est pas une relation d’ordre sur ![]() .
.
![]() Si
Si ![]() ,
,
![]()
![]() et
et ![]()
![]()
![]() .
.
![]()
![]() et
et ![]()
![]()
![]()
![]() si
si ![]() et
et ![]() ,
, ![]() .
.
1.3. Diviseurs et multiples communs
Si ![]() sont des éléments de
sont des éléments de ![]() , on appelle
, on appelle
![]() diviseur commun de
diviseur commun de ![]() tout
tout ![]() tel que
tel que ![]() .
.
👍![]() sont des diviseurs communs à toute famille finie d’éléments de
sont des diviseurs communs à toute famille finie d’éléments de ![]() .
.
![]() multiple commun de
multiple commun de ![]() tout
tout ![]() tel que
tel que ![]() .
.
👍 ![]() est un multiple commun de la famille
est un multiple commun de la famille ![]() .
.
1.4. Division euclidienne
![]() Théorème de division euclidienne
Théorème de division euclidienne
Si ![]() et
et ![]() , il existe un unique couple
, il existe un unique couple ![]() tel que
tel que ![]() où
où ![]()
![]() est le dividende de
est le dividende de ![]() par
par ![]()
![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]() .
.
Remarque : ![]() et
et ![]() .
.
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2. PGCD de deux éléments
2.1. Définition et propriétés du PGCD
![]() Soient
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() .
.
On appelle PGCD de ![]() et
et ![]() et on note
et on note ![]() l’entier naturel défini par
l’entier naturel défini par
![]() si
si ![]()
![]() si
si ![]() ,
, ![]() .
.
Propriétés
![]() Si
Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() ,
,
![]()
![]()
![]() Si
Si ![]() .
.
![]() Si
Si ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
![]() Si
Si ![]() est le reste de la division euclidienne de
est le reste de la division euclidienne de ![]() par
par ![]() ,
, ![]() .
.
![]() si
si ![]() ,
, ![]() et
et ![]() sont dans
sont dans ![]()
![]()
Relation de Bezout : soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() , il existe
, il existe ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]()
⚠️ ![]() et
et ![]() ne sont pas uniques !
ne sont pas uniques !
Si ![]() est solution, pour tout
est solution, pour tout ![]() ,
, ![]() est solution.
est solution.
2.2. Algorithme d’Euclide
![]() Algorithme d’Euclide
Algorithme d’Euclide
Soient ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]()
![]() On note
On note ![]() .
.
![]() Par récurrence :
Par récurrence :
si ![]() , on note
, on note ![]() le reste de la division euclidienne de
le reste de la division euclidienne de ![]() par
par ![]() .
.
![]() Si
Si ![]() est le dernier reste non nul (et donc
est le dernier reste non nul (et donc ![]() ),
), ![]() .
.
![]() Ces calculs permettent de trouver une relation de Bezout par une méthode appelée remontée de l’algorithme d’Euclide :
Ces calculs permettent de trouver une relation de Bezout par une méthode appelée remontée de l’algorithme d’Euclide :
On part de la relation
![]()
écrite sous la forme
![]()
et on remplace ![]() en fonction de
en fonction de ![]() et
et ![]() , ce qui permet d’exprimer
, ce qui permet d’exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() .
.
Et on réitère jusqu’à exprimer ![]() en fonction de
en fonction de ![]() et
et ![]() donc en fonction de
donc en fonction de ![]() et
et ![]() . On obtient une identité de Bezout.
. On obtient une identité de Bezout.
2.3. Algorithme d’Euclide étendu
On se ramène au cas où ![]() et
et ![]() sont dans
sont dans ![]() avec
avec ![]()
On note ![]() ,
, ![]() .
.
On note ![]() le premier reste nul dans la suite des divisions euclidiennes.
le premier reste nul dans la suite des divisions euclidiennes.
Plus précisément si ![]() , on écrit :
, on écrit : ![]() avec
avec ![]() .
.
On suppose ![]() et
et ![]() .
.
Alors les familles définies par
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
sont telles que ![]()
et on retient que
![]() .
.
On peut mener les calculs en tableau :
initialisation
![]()
Calcul de la ligne ![]() si l’on connaît les lignes
si l’on connaît les lignes ![]() et
et ![]() si
si ![]()
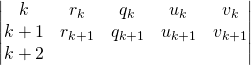
![]() par division euclidienne de
par division euclidienne de ![]() et
et ![]() , on calcule le quotient placé en
, on calcule le quotient placé en ![]() et le reste placé en
et le reste placé en ![]() .
.
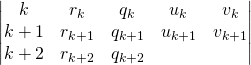
![]() on calcule
on calcule ![]()
et on calcule de même ![]() ce qui permet de compléter la ligne
ce qui permet de compléter la ligne ![]() :
:
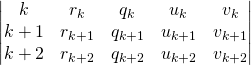
On termine en ayant :
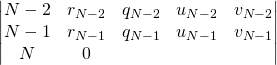
Les calculs de ![]() et
et ![]() sont inutiles.
sont inutiles.
![]() sur la ligne
sur la ligne ![]() donnant le dernier reste non nul, on obtient
donnant le dernier reste non nul, on obtient ![]() ,
, ![]() et
et ![]()
👍 cette méthode est la méthode à utiliser en Python pour programmer le calcul du pgcd et de la relation de Bezout.
Exemple : relation de Bezout pour ![]() et
et ![]() par la remontée de l’algorithme et par l’algorithme d’Euclide étendu.
par la remontée de l’algorithme et par l’algorithme d’Euclide étendu.
Correction : ![]() Algorithme d’Euclide.
Algorithme d’Euclide.
Les divisions successives donnent :
![]()
![]()
![]()
![]()
le reste suivant est nul
Le dernier reste non nul est égal à 1, donc ![]() .
.
![]() Bezout par remontée de l’algorithme d’Euclide
Bezout par remontée de l’algorithme d’Euclide
![]()
![]()
![]()
![]()
![]()
![]()
![]() Par l’algorithme d’Euclide étendu
Par l’algorithme d’Euclide étendu
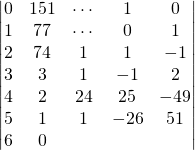
Dans les deux cas, ![]() .
.
3. Nombres premiers entre eux
3.1. Deux nombres premiers entre eux
Définition :
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() . On dit que
. On dit que ![]() et
et ![]() sont premiers entre eux lorsque
sont premiers entre eux lorsque ![]() .
.
👍 ![]() ssi
ssi ![]() sont les seuls diviseurs communs de
sont les seuls diviseurs communs de ![]() et
et ![]() .
.
Propriétés
![]() Théorème de Bezout
Théorème de Bezout
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() .
.
![]() ssi il existe
ssi il existe ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() .
.
![]() Soient
Soient ![]() ,
,
![]() et
et ![]()
![]() .
.
![]() Théorème de Gauss
Théorème de Gauss
Soient ![]() ,
, ![]() et
et ![]() dans
dans ![]() .
.
![]() et
et ![]()
![]()
![]() .
.
![]() Soient
Soient ![]() ,
, ![]() et
et ![]() dans
dans ![]() .
.
![]() divise
divise ![]() ,
, ![]() divise
divise ![]() et
et ![]()
![]()
![]() divise
divise ![]() .
.
![]() Soient
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() et
et ![]() ,
,
alors ![]() et
et ![]()
![]() où
où ![]() et
et ![]() .
.
![]() Pour tout
Pour tout ![]() , il existe un unique couple
, il existe un unique couple ![]() tels que
tels que ![]() avec
avec ![]() .
.
On dit que ![]() est la forme irréductible du rationnel
est la forme irréductible du rationnel ![]() .
.
3.2. Généralisation au cas de ![]() entiers
entiers
![]() Si
Si ![]() ,
, ![]() et
et ![]() ,
,
on appelle PGCD de ![]() et on note
et on note ![]() l’entier naturel défini par
l’entier naturel défini par
![]() si
si ![]() ,
,
![]()
![]() si
si ![]() ,
,
![]()
![]()
![]() Identité de Bezout
Identité de Bezout
Si ![]() ,
, ![]() et
et ![]() ,
,
Il existe ![]() tel que
tel que
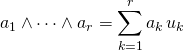 .
.
![]() Si
Si ![]() ,
, ![]() et
et ![]() ,
,
![]() .
.
![]() Si
Si ![]() ,
, ![]() et
et ![]() , on dit que :
, on dit que :
![]()
![]() sont premiers dans leur ensemble si
sont premiers dans leur ensemble si ![]()
![]()
![]() sont premiers 2 à 2 si
sont premiers 2 à 2 si ![]() .
.
![]() Théorème de Bezout
Théorème de Bezout
Si ![]() ,
, ![]() et
et ![]() ,
,
![]() sont premiers dans leur ensemble ssi
sont premiers dans leur ensemble ssi ![]() ,
, 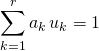 .
.
4. PPCM
![]() Soient
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() .
.
On appelle PPCM de ![]() et
et ![]() et on note
et on note ![]() l’entier naturel défini par
l’entier naturel défini par
![]()
![]()
![]() si
si ![]() ,
, ![]()
Propriétés :
Soient ![]() et
et ![]() de
de ![]()
![]()
![]()
![]()
![]()
![]() si
si ![]() ,
, ![]()
![]() Si
Si ![]() ,
, ![]() et
et ![]() ,
,
on définit le PPCM de ![]() par
par
![]() si
si 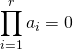 ,
, ![]()
![]() si
si 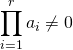 ,
,
![]() est le plus petit
est le plus petit ![]() tel que
tel que ![]() .
.
![]() Si
Si ![]() ,
, ![]() et
et ![]() ,
,
![]() .
.
5. Nombres premiers
5.1. Ensemble ![]()
![]()
![]() est premier lorsque les seuls diviseurs positifs de
est premier lorsque les seuls diviseurs positifs de ![]() sont
sont ![]() et
et ![]() .
.
On note ![]() l’ensemble des nombres premiers.
l’ensemble des nombres premiers.
![]()
![]() est un ensemble infini.
est un ensemble infini.
![]() Si
Si ![]() ,
, ![]() n’est pas premier ssi
n’est pas premier ssi ![]() admet un diviseur premier inférieur ou égal à
admet un diviseur premier inférieur ou égal à ![]() .
.
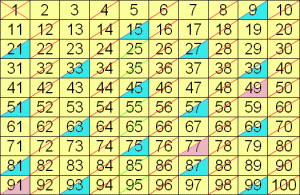
![]() Crible d’Eratosthène
Crible d’Eratosthène
Soit ![]() ,
, ![]() . Pour obtenir la liste des nombres premiers inférieurs ou égaux à
. Pour obtenir la liste des nombres premiers inférieurs ou égaux à ![]() ,
,
![]() on écrit la liste
on écrit la liste ![]() des entiers entre
des entiers entre ![]() et
et ![]() .
.
![]() pour tout
pour tout ![]() , si
, si ![]() n’a pas été supprimé par le passage précédent, on supprime dans la liste
n’a pas été supprimé par le passage précédent, on supprime dans la liste ![]() les multiples de
les multiples de ![]() strictement supérieurs à
strictement supérieurs à ![]() qui n’ont pas encore été supprimés lors des étapes précédentes.
qui n’ont pas encore été supprimés lors des étapes précédentes.
La liste obtenue après le dernier passage est la liste des nombres premiers entre ![]() et
et ![]() .
.
Correction : Dans la liste des entiers de ![]() à
à ![]() ,
,
![]() on barre les nombres pairs entre
on barre les nombres pairs entre ![]() et 100
et 100
![]() on barre les multiples stricts de 3 non encore barrés soit
on barre les multiples stricts de 3 non encore barrés soit ![]()
![]() on barre les multiples stricts de 5 soit
on barre les multiples stricts de 5 soit ![]() multiples de
multiples de ![]() qui n’avaient pas encore été barrés
qui n’avaient pas encore été barrés
![]() on barre les entiers
on barre les entiers ![]() multiples de
multiples de ![]() qui n’avaient pas encore été barrés.
qui n’avaient pas encore été barrés.
Les entiers premiers inférieurs à 100 sont donc ![]()
![]() .
.
5.2. Valuation ![]() -adique
-adique
![]() Si
Si ![]() et
et ![]() ,
,
la valuation ![]() –adique de
–adique de ![]() est
est ![]() .
.
![]() Si
Si ![]() et
et ![]()
![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() , l’ensemble des
, l’ensemble des ![]() tels que
tels que ![]() est fini.
est fini.
On dit que la famille ![]() est une famille d’entiers presque nuls.
est une famille d’entiers presque nuls.
5.3. Décomposition primaire
![]() Soit
Soit ![]() une famille d’entiers presque nulle (c’est à dire
une famille d’entiers presque nulle (c’est à dire ![]() sauf éventuellement pour un nombre fini d’entiers )
sauf éventuellement pour un nombre fini d’entiers )
![]() si
si ![]() , on note
, on note ![]()
![]() si
si ![]() , on note
, on note 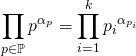
![]() Tout entier
Tout entier ![]() s’écrit d’une et d’une seule façon sous la forme
s’écrit d’une et d’une seule façon sous la forme
![]() .
.
Cette décomposition est appelée décomposition primaire de ![]() .
.
![]() Soient
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]()
![]()
![]() divise
divise ![]() ssi
ssi ![]() ,
, ![]()
![]()
![]()
![]()
![]() .
.
6. Relation de congruence
6.1. Rappels
![]() Si
Si ![]() ,
, ![]() ,
,
![]()
![]()
![]()
définit une relation d’équivalence sur ![]() appelée relation de congruence modulo
appelée relation de congruence modulo ![]() .
.
![]() Pour la relation de congruence modu- lo
Pour la relation de congruence modu- lo ![]() , il y a
, il y a ![]() classes d’équivalence :
classes d’équivalence :
![]() ,
, ![]() .
.
6.2. Propriétés
![]() la relation de congruence modulo
la relation de congruence modulo ![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() vérifiant si
vérifiant si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]() si
si ![]() ,
, ![]()
![]() si
si ![]() ,
, ![]()
![]() Soient
Soient ![]() et
et ![]() .
.
![]() et
et ![]()
![]() .
.
![]() Petit théorème de Fermat
Petit théorème de Fermat
Soit ![]() un nombre premier.
un nombre premier.
![]() pour tout
pour tout ![]() ,
, ![]()
![]() si
si ![]() ne divise pas
ne divise pas ![]() ,
, ![]() .
.
7. Synthèse de méthodes
7.1. Déterminer le pgcd de ![]() et
et ![]() si
si ![]()
Se ramener si nécessaire au cas ![]() et
et ![]() puisque
puisque ![]() .
.
![]() Utiliser l’algorithme d’Euclide.
Utiliser l’algorithme d’Euclide.
![]() Utiliser la décomposition primaire de
Utiliser la décomposition primaire de ![]() et
et ![]() .
.
7.2. Montrer que ![]() si
si ![]()
![]() Utiliser l’algorithme d’ Euclide.
Utiliser l’algorithme d’ Euclide.
![]() Introduire
Introduire ![]() diviseur de
diviseur de ![]() et
et ![]() et montrer que
et montrer que ![]() .
.
![]() Utiliser la décomposition primaire de
Utiliser la décomposition primaire de ![]() et
et ![]() .
.
![]() Supposer qu’il existe
Supposer qu’il existe ![]() qui divise
qui divise ![]() et
et ![]() et démontrer que l’on arrive à une contradiction.
et démontrer que l’on arrive à une contradiction.
![]() Trouver
Trouver ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() .
.
7.3. Utiliser ![]() si
si ![]()
![]()
![]() .
.
![]() Si
Si ![]() divise
divise ![]() et
et ![]() ,
, ![]() .
.
![]() Introduire
Introduire ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() .
.
![]() Si de plus
Si de plus ![]() divise
divise ![]() ,
, ![]() divise
divise ![]() (théorème de Gauss).
(théorème de Gauss).
7.4. Démontrer que ![]() divise
divise ![]()
![]() Trouver
Trouver ![]() tel que
tel que ![]() .
.
![]() Montrer que le reste de la division euclidienne de
Montrer que le reste de la division euclidienne de ![]() par
par ![]() est nul.
est nul.
![]() Montrer que
Montrer que ![]() .
.
![]() Montrer que
Montrer que ![]() .
.
![]() Écrire
Écrire ![]() où
où ![]() sont premiers deux à deux et montrer que
sont premiers deux à deux et montrer que ![]() ,
, ![]() divise
divise ![]() .
.
![]() Montrer que
Montrer que ![]() vérifie
vérifie ![]() ,
, ![]() divise
divise ![]() et que
et que ![]() .
.
![]() Appliquer le théorème de Fermat :
Appliquer le théorème de Fermat :
![]() montrer que
montrer que ![]() est premier et que
est premier et que ![]() avec
avec ![]()
![]() montrer que
montrer que ![]() est premier et que
est premier et que ![]() avec
avec ![]() .
.
7.5. Démontrer que ![]() n’est pas premier
n’est pas premier
![]() Trouver
Trouver ![]() diviseur de
diviseur de ![]() tel que
tel que ![]() .
.
![]() Trouver un entier
Trouver un entier ![]() premier tel que
premier tel que ![]() divise
divise ![]() .
.
(on rappelle qu’un nombre ![]() non premier admet un diviseur premier
non premier admet un diviseur premier ![]() tel que
tel que ![]() ).
).
Complétez vos révisions et vos entraînements en maths au programme de Maths Sup, avec les autres cours en ligne de MPSI, PCSI et PTSI disponibles gratuitement :

