Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Arithmétique Polynômes en Maths Sup MPSI, MP2I
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Arithmétique Polynômes en Maths Sup
Plan :
1.Trouver un PGCD de ![]() et
et ![]()
2. Relation de Bezout
3. Propriétés des PGCD et PPCM
4. Polynômes premiers entre eux
Rappel ![]() et
et ![]() non nuls de
non nuls de ![]() sont associés lorsque’il existe
sont associés lorsque’il existe ![]() tel que
tel que ![]() .
.
1.Trouver un PGCD de  et
et 
On suppose dans ce §, que ![]() et sont non nuls.
et sont non nuls.
On note
![]()
![]() l’ensemble des diviseurs communs à
l’ensemble des diviseurs communs à ![]() et
et ![]() ,
,
![]()
![]() un P.G.C.D de
un P.G.C.D de ![]() et
et ![]() (soit un polynôme de degré maximal élément de
(soit un polynôme de degré maximal élément de ![]() )
)
![]()
![]() le P.G.C.D de
le P.G.C.D de ![]() et
et ![]() , c’est à dire le polynôme unitaire de degré maximal de
, c’est à dire le polynôme unitaire de degré maximal de ![]() .
.
Tous les PGCD de ![]() et
et ![]() sont associés.
sont associés.
![]() M1. Si
M1. Si ![]() et
et ![]() sont scindés sur
sont scindés sur ![]() ,
,
![]() s’ils n’ont pas de racine commune,
s’ils n’ont pas de racine commune, ![]()
![]() s’ils ont
s’ils ont ![]() racines communes et s’écrivent
racines communes et s’écrivent
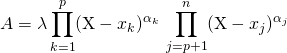
et 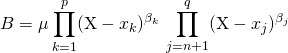
où ![]() sont des éléments de
sont des éléments de ![]() deux à deux distincts.
deux à deux distincts.
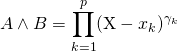
où ![]() .
.
![]() M2. Si
M2. Si ![]() et si les décompositions de
et si les décompositions de ![]() et
et ![]() sous forme de produits de polynômes irréductibles
sous forme de produits de polynômes irréductibles
![]() s’ils n’ont pas de facteur irréductible commun,
s’ils n’ont pas de facteur irréductible commun, ![]()
![]() s’ils ont
s’ils ont ![]() facteurs irréductibles communs et s’écrivent :
facteurs irréductibles communs et s’écrivent :
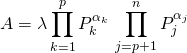
et 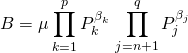
où ![]() sont des polynômes irréductibles 2 à 2 distincts,
sont des polynômes irréductibles 2 à 2 distincts,
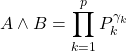 où
où ![]()
![]() M3. En utilisant une relation de Bezout
M3. En utilisant une relation de Bezout
![]() Il existe
Il existe ![]() tel que
tel que ![]() .
.
![]()
![]() ssi
ssi ![]() tel que
tel que ![]() .
.
![]() M4. En utilisant l’algorithme d’Euclide
M4. En utilisant l’algorithme d’Euclide
On se ramène au cas où ![]() ,
,
Poser ![]() et
et ![]() .
.
![]() est le polynôme unitaire proportionnel au dernier reste non nul dans la suite des divisions euclidiennes suivantes :
est le polynôme unitaire proportionnel au dernier reste non nul dans la suite des divisions euclidiennes suivantes :
![]()
![]()
![]()
![]()
…
![]()
![]()
![]() .
.
👍 On rappelle que l’on note ![]() .
.
Si ![]() est associé à
est associé à ![]() .
.
Exemple
Soit ![]() et
et ![]()
Trouver ![]() et une identité de Bezout.
et une identité de Bezout.
Correction :
![]() Algorithme d’Euclide :
Algorithme d’Euclide :
On note ![]() et
et ![]() .
.
![]()
![]() avec
avec ![]() et
et ![]()
![]()
![]() et
et ![]() et
et ![]()
![]()
![]() et
et ![]() donnent :
donnent : ![]() divise
divise ![]() , donc
, donc ![]() .
.
![]() est le dernier reste non nul
est le dernier reste non nul
![]()
![]()
![]() Identité de Bezout en remontant l’algorithme de Bezout :
Identité de Bezout en remontant l’algorithme de Bezout :
![]()
![]()
![]()
En divisant par 21 :
![]() avec
avec ![]()
soit ![]()
et ![]()
soit ![]()
![]() En utilisant l’algorithme étendu sachant que
En utilisant l’algorithme étendu sachant que ![]() et
et ![]()
On définit
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
donne
![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Relation de Bezout
Si ![]() ,
, ![]() et
et
![]()
la relation de Bezout (arithmétique en Maths Sup) est évidente par division par ![]() de cette relation.
de cette relation.
On suppose dans la suite ![]() et
et ![]() non constants.
non constants.
On peut trouver ![]() et
et ![]() de la relation de Bezout :
de la relation de Bezout :
Il existe ![]() tels que
tels que ![]() ,
,
en utilisant l’algorithme d’Euclide étendu
Poser ![]() et
et ![]() avec
avec ![]() .
.
![]() est le polynôme unitaire proportionnel au dernier résultat non nul dans la suite des divisions euclidiennes suivantes :
est le polynôme unitaire proportionnel au dernier résultat non nul dans la suite des divisions euclidiennes suivantes :
on écrit si ![]() avec
avec ![]()
et ![]() .
.
En notant ![]() ,
,
et si ![]() ,
,
![]()
alors pour tout ![]()
![]()
ce qui permet de trouver par récurrence ![]()
et d’en déduire la relation de Bezout.
👍 lorsque ![]() est faible, on peut « remonter » l’algorithme de Bezout petit à petit en partant de
est faible, on peut « remonter » l’algorithme de Bezout petit à petit en partant de ![]()
puis en utilisant ![]()
et en réitérant le principe, jusqu’à tout exprimer en fonction de ![]() et
et ![]() .
.
⚠️ Il n’y a pas unicité du couple ![]() de la relation de Bezout car
de la relation de Bezout car ![]() est aussi solution pour tout
est aussi solution pour tout ![]() .
.
Démo :
On note si ![]() ,
,
![]()
![]()
![]() est vraie par choix de
est vraie par choix de ![]() car
car ![]() et
et ![]() .
.
On suppose que ![]() est vraie et que
est vraie et que ![]() .
.
![]() .
.
En utilisant ![]() ,
,
![]()
![]()
![]()
![]()
et en utilisant les définitions de ![]() et
et ![]() ,
, ![]() ,
,
ce qui prouve ![]() .
.
Exemple
Soient ![]() et
et ![]() .
.
Trouver ![]() et une identité de Bezout.
et une identité de Bezout.
Correction :
![]() Algorithme d’Euclide :
Algorithme d’Euclide :
On note ![]() et
et ![]() .
.
![]()
![]() avec
avec ![]() et
et ![]()
![]()
![]() et
et ![]() et
et ![]()
![]()
![]() et
et ![]() donnent :
donnent : ![]() divise
divise ![]() , donc
, donc ![]() .
.
![]() est le dernier reste non nul
est le dernier reste non nul
![]()
![]()
![]() Identité de Bezout en remontant l’algorithme de Bezout :
Identité de Bezout en remontant l’algorithme de Bezout :
![]()
![]()
![]()
En divisant par 21 :
![]()
avec ![]()
soit ![]()
et ![]()
soit ![]()
![]() en utilisant l’algorithme étendu sachant que
en utilisant l’algorithme étendu sachant que ![]() et
et ![]()
On définit
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
donne
![]() .
.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Propriétés des PGCD et PPCM
![]() Si
Si ![]() ,
,
![]()
![]()
![]()
![]() et
et ![]() sont associés.
sont associés.
![]() Si
Si ![]() sont des éléments non nuls de
sont des éléments non nuls de ![]() , le PGCD de cette famille est le polynôme unitaire noté
, le PGCD de cette famille est le polynôme unitaire noté ![]() qui est le diviseur unitaire commun aux
qui est le diviseur unitaire commun aux ![]() polynômes de degré maximal.
polynômes de degré maximal.
Il existe des polynômes ![]() de
de ![]() tels que
tels que
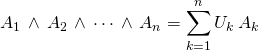 .
.
(Relation de Bezout)
![]() Si
Si ![]() , on appelle PPCM de
, on appelle PPCM de ![]() et
et ![]() tout élément
tout élément ![]() vérifiant les deux conditions :
vérifiant les deux conditions :
![]()
![]() est un multiple de
est un multiple de ![]() et
et ![]()
![]() Si
Si ![]() est un multiple de
est un multiple de ![]() et
et ![]() ,
, ![]() est un multiple de
est un multiple de ![]() .
.
Lorsque ![]() et
et ![]() sont non nuls, tous les PPCM sont associés et on note
sont non nuls, tous les PPCM sont associés et on note ![]() le seul PPCM unitaire.
le seul PPCM unitaire.
![]() Si
Si ![]() ,
,
![]() et
et ![]() sont associés.
sont associés.
4. Polynômes premiers entre eux
![]()
![]() et
et ![]() de
de ![]() sont premiers entre eux
sont premiers entre eux
ssi ![]()
ssi ![]() ,
, ![]() .
.
![]()
![]() de
de ![]() sont premiers entre eux dans leur ensemble
sont premiers entre eux dans leur ensemble
ssi ![]()
ssi Il existe ![]() de
de ![]() tels que
tels que 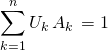 .
.
![]() Si
Si ![]() de
de ![]() sont premiers deux à deux, ils sont premiers entre eux dans leur ensemble.
sont premiers deux à deux, ils sont premiers entre eux dans leur ensemble.
⚠️ la réciproque est fausse.
![]() Théorème de Gauss
Théorème de Gauss
![]() non nuls,
non nuls,
Si ![]() et
et ![]() divise
divise ![]() , alors
, alors ![]() divise
divise ![]() .
.
![]() Soient
Soient ![]() de
de ![]()
![]()
![]() ,
,
alors ![]() .
.
![]()
![]() divise
divise ![]() et si les polynômes
et si les polynômes ![]() sont premiers 2 à 2, alors
sont premiers 2 à 2, alors ![]() divise
divise ![]() .
.
Les mathématiques sont très importantes en Maths Sup, et le coefficient de cette épreuve est très élevé aux concours post-prépa. Adopter les bons réflexes et maîtriser parfaitement les notions de Maths Sup est fondamental pour réussir ces concours. Les cours en ligne et des professeurs particulier de maths sont mis à disposition des étudiants de PTSI, PCSI et MPSI pour les aider dans leurs révisions et les faire progresser durablement. Ainsi, à la fin de ce cours, les étudiants sont invités à consulter et travailler sur les prochains chapitres du programme :

