Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Corrigés: Raisonnement et récurrence
Résumé de cours Exercices Corrigés
Cours en ligne de Maths en Maths Sup
Corrigés- raisonnements et récurrence MPSI, PCSI
1. 1. Manipulation des assertions et quantificateurs
Exercice 1
Soit ![]() une fonction de
une fonction de ![]() dans
dans ![]() .
.
Traduire en termes de quantificateurs les phrases suivantes :
1/ ![]() est majorée.
est majorée.
Corrigé :
![]() est majorée ssi
est majorée ssi
![]() .
.
2/ ![]() n’est pas minorée
n’est pas minorée
Corrigé :
3/ ![]() est bornée.
est bornée.
Corrigé :
Corrigé :
![]()
![]() paire se traduit par
paire se traduit par ![]() .
.
![]()
![]() impaire se traduit par
impaire se traduit par ![]() .
.
![]()
![]() n’est ni paire ni impaire se traduit par
n’est ni paire ni impaire se traduit par
![]() .
.
👍 cette affirmation est équivalente et plus concise que
il existe ![]() tel que
tel que ![]()
ou
il existe ![]() tel que
tel que ![]() .
.
5/ ![]() ne s’annule jamais
ne s’annule jamais
Corrigé :
6/ ![]() est périodique
est périodique
Corrigé :
7/ ![]() est croissante
est croissante
Corrigé :
![]() est croissante se traduit par
est croissante se traduit par
![]() , (
, (![]() ).
).
8/ ![]() est strictement décroissante
est strictement décroissante
Corrigé :
![]() est strictement décroissante se traduit par
est strictement décroissante se traduit par
![]() , (
, (![]() ).
).
9/ ![]() n’est pas monotone
n’est pas monotone
Corrigé :
![]() n’est pas monotone se traduit par
n’est pas monotone se traduit par
![]() ,
, ![]()
ce qui traduit le fait que ![]() et
et ![]() ne sont pas de même signe.
ne sont pas de même signe.
On peut aussi écrire
![]() ,
, ![]() .
.
10/ ![]() n’ est pas la fonction nulle
n’ est pas la fonction nulle
Corrigé :
11/ ![]() ne prend pas deux fois la même valeur
ne prend pas deux fois la même valeur
Corrigé :
![]() ne prend pas deux fois la même valeur
ne prend pas deux fois la même valeur
se traduit par :
si ![]() ).
).
👍 On dit que ![]() est injective.
est injective.
12/ ![]() atteint toutes les valeurs de
atteint toutes les valeurs de ![]() .
.
Corrigé :
![]() prend toutes les valeurs de
prend toutes les valeurs de ![]() se traduit par
se traduit par
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Exercice 2
Si ![]() est une partie non vide de
est une partie non vide de ![]() , traduire en français les propriétés suivantes :
, traduire en français les propriétés suivantes :
Question 1
![]() .
.
Corrigé :
![]() ne contient pas deux éléments consécutifs.
ne contient pas deux éléments consécutifs.
Question 2
![]() est une partie non vide de
est une partie non vide de ![]() vérifiant
vérifiant ![]() .
.
Corrigé :
Si ![]() , le suivant est dans
, le suivant est dans ![]() (ainsi que tous les entiers supérieurs à
(ainsi que tous les entiers supérieurs à ![]() ).
).
Alors si ![]() est le plus petit élément de
est le plus petit élément de ![]() ,
, ![]() .
.
(on admet que toute partie non vide de ![]() possède un plus petit élément).
possède un plus petit élément).
Exercice 3
Que dire de ![]() vérifiant
vérifiant
a) ![]()
b) ![]() ?
?
Corrigé :
On ne peut rien déduire de l’affirmation ![]() puisque toute fonction
puisque toute fonction ![]() vérifie cette condition avec
vérifie cette condition avec ![]() .
.
Si ![]() vérifie b),
vérifie b), ![]() est constante.
est constante.
Exercice 4
Quelles sont les fonctions ![]() vérifiant
vérifiant
a) ![]()
![]()
b) ![]()
![]()
Corrigé :
Les fonctions ![]() vérifiant la condtion a) sont les fonctions affines.
vérifiant la condtion a) sont les fonctions affines.
Toute fonction ![]() vérifie la condition b)
vérifie la condition b)
il suffit de prendre ![]() et
et ![]() .
.
Exercice 5
Soit ![]() et
et
Traduire avec des quantificateurs
a) ![]() sont
sont ![]() réels non nuls.
réels non nuls.
b) ![]() sont
sont ![]() réels non tous nuls
réels non tous nuls
c) ![]() est une famille de réels contenant au moins un 0
est une famille de réels contenant au moins un 0
d) ![]() est une famille de réels contenant un seul 0.
est une famille de réels contenant un seul 0.
Corrigé :
a) ![]() .
.
b) ![]()
et ![]() .
.
c) ![]()
et ![]()
ou
![]() et
et 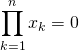 .
.
d) ![]()
et ![]() .
.
ou
![]() ,
, ![]()
et ![]() .
.
Exercice 6
Traduire avec des quantificateurs :
Question 1
Certains réels sont strictement supérieurs à leur carré
Corrigé :
![]() .
.
(c’est le cas pour les réels vérifiant ![]() soit les réels de
soit les réels de ![]() ).
).
Question 2
Étant donnés trois réels non nuls, il y en a au moins deux de même signe
Corrigé :
Il est plus simple de définir les trois réels par la même lettre ![]() indexée.
indexée.
Soient ![]() ,
,
![]() .
.
Exercice 7
Soient ![]() et
et ![]() deux propriétés définies sur un ensemble
deux propriétés définies sur un ensemble ![]() .
.
Les assertions
a) ![]() et
et ![]() )
)
b) (![]() ) et (
) et (![]() )
)
sont-elles équivalentes ?
Corrigé :
Prendre ![]() ,
, ![]() « être pair » et
« être pair » et ![]() « être impair « .
« être impair « .
L’affirmation
(![]() ) et (
) et (![]() )
)
est vraie.
Par contre l’affirmation
![]() et
et ![]() )
)
est fausse car aucun entier n’est à la fois pair et impair.
Les propriétés a) et b) ne sont pas équivalentes. Mais la première propriété implique la deuxième.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
2. Raisonnement par récurrence en maths sup
Exercice 1
Montrer que si ![]() , 3 divise
, 3 divise ![]() .
.
Corrigé :
On établit le résultat par récurrence sur ![]() . On note :
. On note :
![]() si
si ![]() ,
, ![]() divise
divise ![]() .
.
![]()
![]() est vraie car
est vraie car ![]() est divisible par 3.
est divisible par 3.
![]() On suppose que
On suppose que ![]() est vraie
est vraie
![]()
![]()
En utilisant ![]() , il existe
, il existe ![]() tel que
tel que ![]() , on a donc prouvé que
, on a donc prouvé que
![]() est divisible par 3.
est divisible par 3.
![]() est vraie.
est vraie.
![]() La propriété est établie par récurrence.
La propriété est établie par récurrence.
Exercice 2
![]() et si
et si ![]() ,
, ![]() .
.
Conjecturer la valeur de ![]() et le démontrer
et le démontrer
Corrigé :
![]() ,
, ![]() ,
, ![]() et
et ![]()
Ce qui doit suffire pour conjecturer !
Si ![]() , on note
, on note ![]() :
: ![]() .
.
![]()
![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie
est vraie
![]()
![]() ce qui prouve
ce qui prouve ![]() .
.
![]() La propriété est démontrée par récurrence sur
La propriété est démontrée par récurrence sur ![]() .
.
Exercice 3
Soit ![]() .
.
Si ![]() est croissante de
est croissante de ![]() dans
dans ![]() il existe
il existe ![]() tel que
tel que ![]() .
.
Corrigé :
Si ![]() , on note
, on note ![]() : Si
: Si ![]() est croissante de
est croissante de ![]() dans
dans ![]() , il existe
, il existe ![]() tel que
tel que ![]() .
.
![]() Pour
Pour ![]() ,
, ![]() est une fonction croissante de
est une fonction croissante de ![]() dans lui même, donc
dans lui même, donc ![]() et
et ![]() est prouvée.
est prouvée.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
Soit ![]() croissante de
croissante de ![]() dans
dans ![]() .
.
![]() Si
Si ![]() , le résultat est établi avec
, le résultat est établi avec ![]() .
.
![]() Si
Si ![]() ,
, ![]() .
.
La restriction ![]() de
de ![]() à
à ![]() est une fonction croissante de
est une fonction croissante de ![]() dans lui-même, donc d’après
dans lui-même, donc d’après ![]() , il existe
, il existe ![]() tel que
tel que ![]() , donc
, donc ![]() avec
avec ![]() .
.
Par disjonction des cas, on a établi ![]() .
.
![]() La propriété est démontrée par récurrence.
La propriété est démontrée par récurrence.
Exercice 4
Si ![]() est un réel non nul tel que
est un réel non nul tel que ![]() , alors
, alors ![]() .
.
Corrigé :
On suppose que ![]() est un réel non nul tel que
est un réel non nul tel que ![]() et si
et si ![]() , on note
, on note ![]() et
et ![]() .
.
![]()
![]() est vérifiée car :
est vérifiée car : ![]() et
et ![]() .
.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
On note ![]() .
.
![]()
![]()
soit ![]()
comme ![]() sont dans
sont dans ![]() ,
, ![]() .
.
![]() est vraie.
est vraie.
![]() La propriété est démontrée par récurrence.
La propriété est démontrée par récurrence.
Exercice 5
Tout entier ![]() peut s’écrire comme somme de puissances de 2 toutes distinctes.
peut s’écrire comme somme de puissances de 2 toutes distinctes.
Corrigé :
On va procéder par récurrence forte sur ![]() .
.
Si ![]() , on note
, on note ![]() : pour tout entier
: pour tout entier ![]() tel que
tel que ![]() ,
, ![]() est somme de puissances de 2 toutes distinctes.
est somme de puissances de 2 toutes distinctes.
![]()
![]() est vraie car
est vraie car ![]() .
.
![]() Soit
Soit ![]() tel que
tel que ![]() soit vraie.
soit vraie.
![]() Si
Si ![]() est pair, alors
est pair, alors ![]() avec
avec ![]() car
car ![]() ,
, ![]() s’écrit comme somme de puissances de 2 toutes distinctes,
s’écrit comme somme de puissances de 2 toutes distinctes,
![]()
avec ![]()
donc ![]() est la somme de puissances de 2 toutes distinctes.
est la somme de puissances de 2 toutes distinctes.
![]() Si
Si ![]() est impair, alors
est impair, alors ![]() avec
avec ![]() ,
, ![]() s’écrit comme somme de puissances de 2
s’écrit comme somme de puissances de 2
![]()
avec ![]() ,
,
![]()
et ![]() est la somme de puissances de 2, 2 à 2 distinctes.
est la somme de puissances de 2, 2 à 2 distinctes.
On a prouvé que ![]() est vraie.
est vraie.
![]() La propriété est démontrée par récurrence.
La propriété est démontrée par récurrence.
Exercice 6
Trouver l’erreur dans le raisonnement par récurrence suivant.
Soit si ![]() ,
, ![]() » dans toute partie de
» dans toute partie de ![]() entiers, tous les éléments ont même parité. »
entiers, tous les éléments ont même parité. »
![]()
![]() est vraie de façon évidente.
est vraie de façon évidente.
![]() Soit
Soit ![]() tel que
tel que ![]() soit vraie.
soit vraie.
Soit ![]() une partie de
une partie de ![]() entiers que l’on range par ordre strictement croissant.
entiers que l’on range par ordre strictement croissant.
On note ![]() (resp
(resp ![]() ) la partie de
) la partie de ![]() formée des
formée des ![]() plus petits (resp.
plus petits (resp. ![]() plus grands) éléments de
plus grands) éléments de ![]() .
.
D’après l’hypothèse ![]() , les éléments de
, les éléments de ![]() ont même parité ainsi que les éléments de
ont même parité ainsi que les éléments de ![]() .
.
Or l’entier ![]() numéro
numéro ![]() est à la fois dans
est à la fois dans ![]() et
et ![]() , donc les éléments de
, donc les éléments de ![]() et de
et de ![]() ont la parité de
ont la parité de ![]() , donc tous les éléments de
, donc tous les éléments de ![]() ont même parité.
ont même parité.
![]() Par récurrence, toute partie finie non vide de
Par récurrence, toute partie finie non vide de ![]() est formée d’éléments de même parité.
est formée d’éléments de même parité.
Corrigé :
La propriété est fausse car si ![]() , les ensembles
, les ensembles ![]() et
et ![]() n’ont pas d’élément commun, ce n’est que pour
n’ont pas d’élément commun, ce n’est que pour ![]() , que l’on peut dire que le
, que l’on peut dire que le ![]() -ième élément est à la fois dans
-ième élément est à la fois dans ![]() et
et ![]() .
.
Exercice 7
Soit pour ![]() ,
, ![]() : 5 divise
: 5 divise ![]()
Question 1
La propriété ![]() est héréditaire.
est héréditaire.
Corrigé :
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
comme ![]() où
où ![]() ,
,
![]() est divisible par 5.
est divisible par 5.
La propriété ![]() est héréditaire.
est héréditaire.
Question 2
![]() est vraie pour tout
est vraie pour tout ![]() .
.
Corrigé :
Pour ![]() , 5 ne divise pas
, 5 ne divise pas ![]() .
.
On peut démontrer que ![]() ne divise jamais
ne divise jamais ![]() .
.
On démontre que le chiffre des unités de ![]() est
est ![]() lorsque
lorsque ![]() .
.
Si ![]() , on note
, on note ![]() : il existe
: il existe ![]() tel que
tel que ![]() .
.
![]() est vraie car
est vraie car ![]()
On suppose que ![]() est vraie, on écrit qu’il existe
est vraie, on écrit qu’il existe ![]() tel que
tel que ![]()
![]()
![]() .
.
Par récurrence, le chiffre des unités de ![]() est toujours un 7 ; donc
est toujours un 7 ; donc ![]() n’est pas divisible par
n’est pas divisible par ![]() pour tout
pour tout ![]() .
.
⚠️ Il est important de ne pas oublier de vérifier correctement l’initialisation de la récurrence !
Exercice 8
Soit ![]()
et ![]() .
.
On note si ![]() ,
,
![]() :
: ![]() .
.
Question 1
![]() est héréditaire.
est héréditaire.
Corrigé :
On suppose que ![]() est vraie avec
est vraie avec ![]() , alors
, alors ![]() et
et ![]() sont des rationnels, donc
sont des rationnels, donc ![]() est rationnel par somme de rationnels.
est rationnel par somme de rationnels.
Question 2
Si ![]() , on a prouvé par récurrence forte que
, on a prouvé par récurrence forte que ![]() est rationnel pour tout
est rationnel pour tout ![]()
Corrigé :
En choisissant ![]() , il est alors évident que
, il est alors évident que ![]() n’est pas rationnel.
n’est pas rationnel.
Comme ![]() est fausse, la propriété n’est pas vraie par récurrence.
est fausse, la propriété n’est pas vraie par récurrence.
Conclusion
⚠️ Il est conseillé pour ne pas se faire piéger par une telle erreur, de démontrer la propriété par récurrence double et non par récurrence forte (ce qui risque l’oubli de la vérification de la propriété pour ![]() ).
).
3. Sur la suite de Fibonacci en maths sup
On considère la suite ![]() (suite de Fibonacci) définie par
(suite de Fibonacci) définie par ![]() et, pour tout
et, pour tout ![]() .
.
Question 1
La suite ![]() vérifie :
vérifie :
![]() .
.
Corrigé :
Si ![]() et
et ![]() , on note
, on note ![]() .
.
![]() .
.
![]()
![]() et
et ![]() , donc
, donc ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie où
est vraie où ![]() est fixé et vérifie
est fixé et vérifie ![]() .
.
![]()
puis ![]() , donc
, donc ![]() .
.
On a établi ![]() .
.
La propriété est démontrée par récurrence sur ![]() .
.
Question 2
La suite ![]() vérifie :
vérifie :
![]() .
.
Corrigé :
Pour tout ![]() on note
on note
![]() :
: ![]() .
.
et on note ![]() .
.
Dans cette question, il est inutile d’utiliser une hypothèse de récurrence double.
![]()
![]()
donc ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie
est vraie
![]()
![]()
![]()
![]()
![]() en utilisant
en utilisant ![]() .
.
![]() est vraie, donc la propriété est démontrée par récurrence.
est vraie, donc la propriété est démontrée par récurrence.
Question 3
La suite ![]() vérifie pour tout
vérifie pour tout ![]() ,
,
![]() .
.
Corrigé :
On fixe ![]() et on utilise une récurrence double sur l’entier
et on utilise une récurrence double sur l’entier ![]() .
.
Soit si ![]() ,
, ![]() :
: ![]() et
et ![]() .
.
![]() Pour
Pour ![]() , (
, (![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
donc ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
Par somme des relations :
![]() et
et ![]() ,
,
on obtient
![]()
![]()
ce qui donne
![]() .
.
On a prouvé ![]() .
.
La propriété est démontrée par récurrence.
Question 4
On note ![]() et
et ![]() .
.
![]() .
.
Corrigé :
On note ![]() et
et ![]()
![]() soit
soit ![]() :
: ![]()
et ![]() .
.
![]() Pour
Pour ![]()
![]()
![]() .
.
On a prouvé que ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
En utilisant la somme des deux relations
![]()
![]()
Puis
![]()
![]()
![]()
donc ![]() .
.
![]()
![]()
![]()
![]() .
.
On a prouvé que
![]() .
.
On a donc établi ![]() .
.
La propriété est établie par récurrence.
4. Autres types de raisonnements
Exercice 1
Démontrer que si ![]() est la somme de deux carrés d’entiers, alors le reste de la division euclidienne de
est la somme de deux carrés d’entiers, alors le reste de la division euclidienne de ![]() par 4 est toujours différent de 3.
par 4 est toujours différent de 3.
Corrigé :
On écrit ![]() où
où ![]() , on raisonne par disjonction des cas.
, on raisonne par disjonction des cas.
![]()
![]() et
et ![]() sont pairs, soit
sont pairs, soit ![]() et
et ![]() où
où ![]() .
.
![]() .
.
Le reste de la division de ![]() par 4 est nul.
par 4 est nul.
![]() L’un est pair et l’autre impair.
L’un est pair et l’autre impair.
Par symétrie, on peut supposer que ![]() est pair et
est pair et ![]() est impair et écrire
est impair et écrire ![]() ,
, ![]() où
où ![]() .
.
![]()
![]() .
.
Le reste de la division de ![]() par 4 est égal à 1.
par 4 est égal à 1.
![]()
![]() et
et ![]() sont impairs, soit
sont impairs, soit ![]() et
et ![]() où
où ![]() .
.
![]()
![]()
Le reste de la division de ![]() par 4 est égal à 2.
par 4 est égal à 2.
Par disjonction des cas, le reste de la division de ![]() par 4 n’est pas égal à 3.
par 4 n’est pas égal à 3.
Exercice 2
Pour tout ![]() ,
, ![]() est divisible par 6
est divisible par 6
Corrigé :
![]() On remarque que
On remarque que ![]() et
et ![]() sont deux entiers consécutifs, l’un est pair et l’autre impair, donc
sont deux entiers consécutifs, l’un est pair et l’autre impair, donc ![]() est pair, alors
est pair, alors ![]() est divisible par 2.
est divisible par 2.
![]() On démontre que
On démontre que ![]() est divisible par 3
est divisible par 3
![]() si
si ![]() où
où ![]() ,
, ![]() est un multiple de
est un multiple de ![]() , donc est divisible par 3.
, donc est divisible par 3.
![]()
![]() où
où ![]() ,
,
![]() est divisible par 3, donc
est divisible par 3, donc ![]() l’est aussi .
l’est aussi .
![]()
![]() où
où ![]() ,
,
![]() est divisible par 3, donc
est divisible par 3, donc ![]() l’est aussi .
l’est aussi .
Par disjonction des cas, ![]() est divisible par 3.
est divisible par 3.
![]() est divisible par 2 et 3, donc divisible par 6.
est divisible par 2 et 3, donc divisible par 6.
👍 Aviez vous pensé à démontrer la divisibilité par 2 puis par 3 (ce qui est plus rapide que de démontrer que la propriété est vraie par disjonction de 6 cas) ?
Exercice 3
Si ![]() et
et ![]() sont réels,
sont réels,
![]()
![]() .
.
Corrigé :
On raisonne par disjonction des cas :
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
soit ![]() .
.
![]()
![]()
soit ![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
soit ![]() .
.
![]()
![]()
soit ![]() .
.
On a établi les relations par disjonction des cas.
Exercice 4
Déterminer l’ensemble des fonctions ![]() de
de ![]() dans
dans ![]() telles que
telles que ![]() ,
, ![]() .
.
Corrigé :
![]() Analyse
Analyse
Si ![]() est solution, en prenant
est solution, en prenant ![]()
![]() donc
donc ![]() ou
ou ![]() .
.
![]() Si
Si ![]() ,
, ![]() donc
donc ![]()
![]() Si
Si ![]() ,
, ![]() donc
donc ![]() .
.
Il y a au plus deux solutions : les fonctions constantes égales à 0 et à 1.
![]() Synthèse
Synthèse
![]() Si
Si ![]() ,
,
![]() ,
, ![]() .
.
![]() Si
Si ![]() ,
,
![]() ,
, ![]() .
.
Le problème admet exactement deux solutions.
Exercice 5
Déterminer les fonctions ![]() telles que pour tout réel
telles que pour tout réel ![]() ,
, ![]()
Corrigé :
On suppose que ![]() est solution, en remplaçant
est solution, en remplaçant ![]() par
par ![]() , pour tout réel
, pour tout réel ![]() ,
, ![]()
relation que l’on multiplie par ![]()
![]()
puis en utilisant la définition de ![]() :
: ![]()
on obtient ![]()
en réordonnant ![]()
sachant que pour tout réel ![]() ,
, ![]() , on obtient
, on obtient ![]() .
.
![]() Synthèse Soit
Synthèse Soit ![]() .
.
Pour tout réel ![]() ,
, ![]()
donc ![]() est solution.
est solution.
Le problème admet une unique solution, la fonction constante égale à 1.
Exercice 6
Déterminer toutes les fonctions ![]() telles que,
telles que,
![]()
![]() .
.
Corrigé :
On va raisonner par analyse-synthèse en déterminant des conditions nécessaires sur ![]() qui vérifie cette équation, puis en vérifiant que ces conditions sont suffisantes.
qui vérifie cette équation, puis en vérifiant que ces conditions sont suffisantes.
![]() Analyse : soit
Analyse : soit ![]() une fonction vérifiant cette condition.
une fonction vérifiant cette condition.
![]() En choisissant
En choisissant ![]() , on obtient
, on obtient ![]() , ce qui entraîne
, ce qui entraîne ![]() ou
ou ![]() .
.
![]() En choisissant ensuite
En choisissant ensuite ![]() et
et ![]() , on a
, on a ![]() , ce qui interdit
, ce qui interdit ![]() . On a donc
. On a donc ![]() (et aussi
(et aussi ![]() ).
).
![]() Enfin, fixant
Enfin, fixant ![]() , on obtient que pour tout
, on obtient que pour tout ![]() , on a
, on a ![]() .
.
On a donc prouvé que si ![]() est solution de l’équation, alors, pour tout réel
est solution de l’équation, alors, pour tout réel ![]() ,
, ![]() .
.
![]() Synthèse : Soit
Synthèse : Soit ![]() .
.
Alors, ![]() , on a
, on a
![]()
![]()
et ![]()
ce qui prouve bien que ![]() est solution de l’équation.
est solution de l’équation.
En conclusion, l’équation admet une solution unique : la fonction ![]() donnée par
donnée par ![]() .
.
Travaillez tous les chapitres de maths de MPSI, PCSI et PTSI grâce à nos divers cours en ligne dont :

