Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours en ligne Maths en Maths Sup

Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Cours : Dérivées en Maths Sup MPSI, MP2I, PTSI et PCSI

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Maths Sup

Résumé de cours et méthodes – dérivées en Maths Sup

Plan :

Les calculs de dérivées ont été abordés dans le chapitre sur les fonctions numériques.

On le complète dans ce chapitre.

1. Dérivabilité en un point
2. Calculer une dérivée $n$ -ième
3. Propriétés des dérivées
4. Utiliser le théorème de Rolle
5. Utiliser le théorème des accroissements finis

Si vous avez des difficultés sur ces notions ou avez pris du retard dans votre classe de maths sup, n’hésitez pas à faire appel à nos professeurs particuliers de maths pour progresser et réussir votre prépa scientifique.

1. Dérivabilité en un point en MPSI, MP2I, PCSI et PTSI

Pour démontrer qu’une fonction $f$ est dérivable en un point $a$ ,

M1. utiliser les théorèmes sur les fonctions dérivables (somme, produit, quotient, composée, fonction réciproque).

M2. utiliser la limite du taux d’accroissement, c’est à dire chercher la limite en $a$ de $\displaystyle x \mapsto \frac {f(x) - f(a) } {x - a}$ .

Exemple 1 : $f$ définie par $\quad \displaystyle f(x) = x^2 \, \sin \left ( \frac 1 x \right )$ et $f(0) = 0$
est dérivable en $0$ .

M3. trouver un développement limité d’ordre 1 de $f$ en $a$ , c’est -à-dire trouver $\alpha$ et $\beta$ dans $\mathbb{K}$ tels que $\quad f(x) \underset{x \to a} = \alpha + \beta (x - a) + \textrm{o} (x - a)$ .

Si $f (a)$ est défini, on vérifie que $\alpha = f(a)$ : la fonction $f$ est alors continue en $a$ .

Si $f(a)$ n’est pas défini, on prolonge $f$ par continuité en $a$ par $f(a) = \alpha$ et on calcule le taux d’accroissement de $f$ en $a$ :

$\displaystyle \frac {f(x) - f(a) } {x - a} \underset{x \to a} = \beta + \textrm{o} (1)$ ,

Il admet $\beta$ pour limite en $a$ , $f$ est dérivable en $a$ et $f ' (a) = \beta$ .

M4. appliquer le théorème de la limite de la dérivée.

A vérifier correctement les hypo- thèses :

Si $f$ est continue sur $[a ,\, b]$ à valeurs dans $\mathbb{K}$ et dérivable sur $]a , \, b[$ et si $f '$ admet une limite finie $L$ en $a$ , $f$ est dérivable à droite en $a$ et $f '(a) = L$ .

Il ne faut pas parler de prolongement de la dérivée par continuité mais du théorème de la limite de la dérivée.

Inconvénients de la méthode :

a) elle oblige à calculer $f ' (x)$ pour $x \neq a$ et à trouver la limite de $f ' (x)$ en $a$ . Bien souvent $f ' (x)$ est plus compli- qué que $f(x)$ . On a donc théoriquement plus de travail qu’en utilisant l’une des trois premières méthodes.

b) $f '$ peut ne pas avoir de limite en $a$ alors que $f ' (a)$ existe ( dans ce cas, le calcul de $f '$ et la recherche de sa limite sont du temps perdu ).

Avantages de la méthode

a) dans certains cas, $f ' (x)$ est plus simple que $f(x)$ ( c’est en particulier le cas lorsque $f$ est définie par une inté- grale dont les bornes dépendent de $x$ )

b) lorsque l’on demande de prouver que $f$ est dérivable en $a$ et que $f '$ est continue en $a$ : en utilisant M4, on prouve en effet non seulement que $f$ est dérivable en $a$ mais aussi que $f '$ admet $f '(a$ ) pour limite en $a$ , donc que $f '$ est continue en $a$ .

Exemple 2 : $f$ définie par $\quad \displaystyle f(x) = x^2 \, \sin \left ( \frac 1 x \right )$ et $f(0) = 0$ .
Peut-on lui appliquer le théorème de la limite de la dérivée ?

Exemple 3

Soit $f$ définie par $f(x) = \displaystyle \frac {\sin x} x$ si $x \neq 0$ et $f(0) = 1$ .

Montrer que $f$ est dérivable sur $\mathbb{R}$ de dérivée continue.

COURS DE MATHS

Nous avons recruté pour vous les meilleurs professeurs particuliers de maths

S'EXERCER ET APPRENDRE

Avis Google France ★★★★★ 4,8 sur 5

2. Calculer une dérivée $n$ -ième

2.1. En utilisant les dérivées classiques :

Des dérivées successives à savoir calculer rapidement

Si $n \in \mathbb{N}$ , $a \in \mathbb{C}$ et $u : x \mapsto (x - a) ^n$
… si $p \leq n$ , $\quad \quad u ^{(p)}(x) = \displaystyle \frac {n!} {(n - p)!} (x - a)^{n - p}$
… si $p >n$ , $u ^{(p)}(x) = 0$ .

Si $a \in \mathbb{C}$ et $u : x \mapsto \displaystyle \frac 1 {x - a}$

Si $n \in \mathbb{N}$ , $u ^{(n)}(x) = \displaystyle \frac {n!\, (-1) ^n } {(x - a) ^{n + 1}} .$

Si $a \in \mathbb{C}$ et $u : x \mapsto \displaystyle \frac 1 {a - x}$

Si $n \in \mathbb{N}$ , $u ^{(n)}(x) = \displaystyle \frac {n!} {(a - x) ^{n + 1}}$ .

Si $(a , b) \in \mathbb{R}^2$ , $f : x \mapsto \cos(a\, x + b)$ et $g : x \mapsto \sin(a\, x + b)$ , pour tout $n \in \mathbb{N}$ et $x \in \mathbb{R}$ ,

$f ^{(n)}(x) = \displaystyle a ^n \cos \left (a \, x + b + n \, \frac {\pi} 2 \right )$

$g ^{(n)}(x) = \displaystyle a ^n \sin \left (a \, x + b + n \, \frac {\pi} 2 \right )$ .

2.2. En utilisant des sommes

Par calcul de la dérivée $n$ -ième d’une somme (en particulier utilisation d’une décomposition en éléments simples) :

Exemple

Dérivées $n$ -ièmes de $\displaystyle x \mapsto \frac 1 { 1 - x^2}$ de $x \mapsto \textrm{Arctan} (x)$ ou de $x \mapsto \ln(1 + x^2)$

2.3. Par utilisation de fonctions à valeurs complexes

Soit $(a, b) \in \mathbb{R}^2$ .

$f : x \mapsto \textrm{e} ^{a \, x} \cos(b\, x)$

et $g : x \mapsto \textrm{e} ^{a \, x} \sin(b\, x)$ .

On introduit $F : x \mapsto \textrm{e} ^{( a + \, \textrm{i} \, b ) x}$ .

$\quad \; f = \mathcal{R}e (F)$ et $g = \mathcal{I}m(F)$ .

Donc $f^{(n)} (x) = \mathcal{R}e (F^{(n)}(x))$ et $g^{(n)} (x) = \mathcal{I}m(F ^ {(n)}(x))$

avec $F ^{(n)}(x) = (a + \, \textrm{i} \, b) ^n F(x)$ , il reste à trouver la forme trigonométrique $\rho \,\textrm{e} ^{ \textrm{i} \, \theta}$ de $a + \, \textrm{i} \, b$ pour calculer $\quad \quad (a + \, \textrm{i} \, b)^n = \rho^n \,\textrm{e} ^{ \textrm{i} \,n \, \theta}$ .

2.4. Par utilisation de la formule de Leibniz en MPSI, PCSI, PTSI et MP2I

Énoncé :

Soient $f$ et $g$ deux fonctions définies sur l’intervalle $I$ à valeurs dans $\mathbb{K}$ , $n$ fois dérivables en $a \in I$ où $n \in \mathbb{N}^*$ .

La fonction $f \, g$ est $n$ fois dérivable en $a$ et

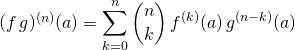$(f \, g) ^{(n)} (a) = \displaystyle \sum _{k = 0} ^n \binom {n} {k} \, f ^{(k)} (a) \, g ^{(n - k)}(a)$ en notant $f ^{(0)} = f$ et $g ^ {(0)} = g$ .

L’utilisation de la formule de Leibniz sera simple, si l’on peut écrire $f = u\, v$ , les dérivées successives de $u$ et $v$ étant faciles à calculer, et c’est encore plus facile lorsque les dérivées successives de $u$ sont nulles à partir d’un rang $k_0$ .

Exemple :

Dérivée $n$ -ième de $f: x \mapsto x^2 \, \textrm{e} ^{a \, x}$ .

2.5. Par utilisation du théorème de classe $C ^k$ par prolongement

Soit $I$ un intervalle et $a$ un point de $I$ ou une borne de $I$ . Soit $n \in \mathbb{N} ^*$ .

Si $f$ est de classe $C ^k$ sur $I \setminus \{a \}$ et si pour tout $k \in [\![0 , n]\!], \, f ^ {(k)}$ admet une limite finie en $a$ , alors $f$ admet un prolongement de classe $C ^k$ sur $I$ .

3. Propriétés des dérivées en maths sup

3.1. Dérivées et parité

La dérivée d’une fonction paire est impaire.

Il suffit de dériver la relation : $\quad \quad\forall \, x \in I, f (- x) = f(x)$ ,

$\forall \, x \in I, \, - f' (- x) = f(x)$ .

$\bullet$ La dérivée d’une fonction impaire est paire

Il suffit de dériver la relation : $\quad \quad \forall \, x \in I, f (- x) = - f(x)$ ,

$\forall \, x \in I, \, - f' (- x) = - f(x)$ .

$\bullet$ Si $f$ est une fonction paire et $n$ fois dérivable sur $I$ , $f^{ (n)}$ a la parité de $n$ .

Si $f$ est une fonction impaire et $n$ fois dérivable sur $I$ , $f^{ (n)}$ a la parité contraire à celle de $n$

3.2. Dérivée et périodicité

Si $f$ est dérivable sur $\mathbb{D}$ et périodique de période $T$ , $f'$ est $T$ -périodique.

On dérive la relation $\quad \quad \forall\, x \in \mathbb{D}, \, f(x + T) = f(x)$ .

On obtient : $\quad \quad \forall\, x \in \mathbb{D}, \, f'(x + T) = f'(x)$ .

3.3. Trouver une relation entre les dérivées successives d’une fonction

M1 par récurrence si la formule est donnée ou conjecturée.

M2 sans utiliser une récurrence.

On cherche une équation différentielle d’ordre 1 (ou 2) vérifiée par $f$ et on l’écrit de façon à appliquer facilement la formule de Leibniz.

Exemple : relation entre les dérivées successives de $f : x \mapsto \textrm{Arctan}(x)$ .

AVOIR LES MEILLEURS PROFS DE MATHS

C'est gagner en autonomie

4. Utiliser le théorème de Rolle en prepa maths sup

Rappel du théorème de Rolle :

Soient $a$ et $b$ deux réels tels que $a < b$ .

Si $f$ est continue sur $[a , \,b]$ à valeurs dans $\mathbb{R}$ , dérivable sur $]a ,\, b[$ et si $f(a) = f(b)$ , il existe $c \in \; ]a ,\, b[$ tel que $f '(c) = 0$ .

M1. Pour prouver qu’une dérivée s’annule en un point $c$ :

M1.1. essayer de déterminer un segment $[a ,\, b]$ sur lequel on puisse appliquer le théorème de Rolle.

M1.2. essayer de démontrer que $f$ admet un extremum relatif en $c$ , le point $c$ étant intérieur à l’intervalle.
rappel du théorème :

Soit $f$ définie sur l’intervalle $I$ à valeurs dans $\mathbb {R}$ et $a$ un point de $I$ distinct des bornes ; si $f$ est dérivable en $a$ et si

$f$ admet un extremum relatif en $a$ , $f '(a) = 0$ .

Exemple

Soit $f : x \mapsto (x^2 - 1) \textrm{Arcsin}(x)$ .

Montrer que la dérivée de $f$ s’annule au moins deux fois sur $]- 1 , \, 1[$ .

On rappelle que l’on appelle zéro d’une fonction $g$ sur $I$ tout $c \in I$ tel que $g(c) = 0$ .

M2. Pour minorer le nombre de zéros de $f '$ lorsque l’on sait que $f$ a $n$ zéros dans un intervalle $I$ et est à valeurs dans $\mathbb{R}$ .

On range les $n$ zéros de $f$ par ordre strictement croissant : $\quad \quad \quad x_1 < x_2 < \, \cdots \, < x_n\,$ .

$f$ vérifie les conditions du théorème de Rolle sur chaque intervalle $[x_i \, , \,x_{i + 1}]$ où $1 \leq i \leq n - 1$ ,

il existe $y_i \in\; ]x_i\, ,\, x_{i + 1}[$ tel que $f '(y_i) = 0$ .

On a donc démontré que $f '$ admet au moins $n - 1$ zéros (les $y_i$ sont dans des intervalles 2 à 2 disjoints) dans l’intervalle $I$ .

5. Utiliser le théorème des accroissements finis en MPSI, PTSI, MP2I et PCSI

5.1. Rappel du théorème des accroissements finis

Soient $a$ et $b$ deux réels tels que $a < b$ .

Si $f$ est définie sur $[a ,\, b]$ à valeurs dans $\mathbb{R}$ , continue sur $[a ,\, b]$ , dérivable sur $]a ,\, b[$ , il existe $c \in \; ]a ,\, b[$ tel que $\quad \quad \quad \displaystyle \frac {f(b) - f(a)} {b - a} = f'(c)$ .

Autres écritures

Dans la suite, on note $I$ un intervalle et $\overset{\circ} I$ l’intervalle $I$ privé de ses bornes.

$\ast$ Si $f$ est continue sur $I$ à valeurs réelle, dérivable sur $\overset{\circ} I$ , pour tout $a$ et $b$ de $I$ avec $a \neq b$ , il existe $c$ strictement compris entre $a$ et $b$ tel que

$\quad \quad f(b) - f(a) = (b - a) f '(c)$ .

$\ast$ Si $f$ est continue sur $I$ à valeurs réelles, dérivable sur $\overset{\circ} I$ , pour tout $a$ de $I$ et tout réel $h$ tel que $a + h \in I$ , il existe $\theta \in\; ]0 ,\, 1[$ tel que $\quad f(a + h ) - f(a) = h f '(a + \theta \, h)$ .

5.2. Pour démontrer des inégalités

M1. Par utilisation de l’inégalité des accroissements finis :

$\ast$ si $f$ est continue sur $[a , \, b]$ , dérivable sur $]a ,\, b[$ à valeurs dans $\mathbb{R}$ et si pour tout $x$ de $]a ,\, b[$ , $m \leq f '(x) \leq M$ ,

alors $m (b - a)\leq f (b) - f(a)\leq M (b - a)$ .

$\ast$ si $f$ est dérivable sur l’intervalle $I$ à valeurs dans $\mathbb{R}$ et si $f '$ est bornée sur $I$ , en notant $M= \displaystyle \sup _{t \in I} \vert f'(t) \vert$ ,

Pour tous $x$ et $y$ de $I$ ,

\quad \quad \quad \displaystyle \vert f(x) – f(y) \vert \leq M \vert x -y \vert \; $. On dit que$ f $est$ M $-lipschitzienne sur$ I $. M2. Démonstration d'inégalités strictes (ou larges) en utilisant le théorème des accroissements finis. Exemple Si$ f $est continue sur$ [a ,\, b] $à valeurs dans$ \mathbb{R} $, dérivable sur$ [a ,\, b] $et si$ f ‘ $est strictement croissante sur$ [a , \, b] $,$ (b – a)\, f ‘(a) < f(b) – f(a) \quad \quad \quad \quad \quad \quad \quad \quad < (b – a) \, f ‘(b) $. Exemple : si$ x > 0 $,$ \displaystyle \frac 1 {x + 1} < \ln(x + 1) – \ln(x) < \frac 1 x $. Exemples d'inégalités à savoir prouver Si$ (x , \,y) \in \mathbb{R}^2 $,$ \ast\vert \sin x – \sin y \vert \leq \vert x – y \vert $\text{[math]}$ \ast\vert \cos x – \cos y \vert \leq \displaystyle \frac {x^2} 2 $\text{[math]}$ \ast\vert \textrm {e} ^x – 1 \vert \leq \vert x \vert \, \textrm{e} ^{\vert x \vert } $.$ \ast $pour tout$ x \geq 0 $,$ \vert \textrm {e} ^{-x} – 1 \vert \leq \vert x \vert $. Inégalité des accroissements finis pour les fonctions à valeurs complexes Si$ f $est de classe$ C ^1 $sur l'intervalle$ I $, pour tout$ (a , b) \in I^2 $avec$ a < b $,$ \vert f(b) – f(a) \vert \leq \displaystyle (b- a) \; \sup _{t \in [a , b]} \vert f ‘(t) \vert . $Il n'y a pas de théorème des accroissements finis pour les fonctions à valeurs complexes. L'inégalité des accroissements finis au programme exige que la fonction soit de classe$ C^1 $pour les fonctions complexes. 5.3. Pour les variations des fonctions Application du théorème des accroissements finis à la variation d'une fonction : M4. Soit$ f $une fonction continue sur l'intervalle$ I $à valeurs dans$ \mathbb{R} $, on suppose que$ f $est dérivable sur$ \overset{\circ} I $(intervalle$ I $privé de ses bornes)$ \astf $est constante sur$ I $si, et seulement si, pour tout$ x $de$ \overset{\circ} I $,$ f ‘(x) = 0 $.$ \astf $est croissante sur$ I $si, et seule- ment si, pour tout$ x $de$ \overset{\circ} I $,$ f ‘(x) \geq 0 $.$ \astf $est décroissante sur$ I $si, et seu- lement si, pour tout$ x $de$ \overset{\circ} I $,$ f ‘(x)\leq 0 $.$ \astf $est strictement croissante sur$ I $si, et seulement si,$ \forall\, x \in I, \, f'(x) \geq 0 $et il n'existe pas d'intervalle ouvert non vide inclus dans$ \overset{\circ} I $sur lequel$ f’ $s'annule. En particulier si pour tout$ x $de$ \overset{\circ} I $,$ f ‘(x) > 0 $,$ f $est strictement croissante sur$ I $. 5.4. Pour simplifier une expression à l'aide d'une dérivée $ \ast $On cherche le domaine de continuité$ \mathcal{D} $de$ f $, puis l'<a href="https://groupe-reussite.fr/ressources/cours-en-ligne-ensembles-et-applications-maths-sup/">ensemble</a>$ \mathcal{D}’ $des points où elle est dérivable (attention aux fonctions$ \textrm{Arcsin} $et$ \textrm{Arccos} $non dérivables en$ \pm1 $et aux racines non dérivables en 0).$ \ast $On calcule la dérivée de$ f $et on cherche à reconnaître une dérivée connue.$ \ast $On partage le domaine$ \mathcal{D} $en interval- les sur lesquels on peut appliquer le résultat suivant : Si$ f – g $est continue sur l'intervalle$ I $, dérivable sur$ \overset {\circ}{I} $, de dérivée nulle, alors il existe un réel$ C $tel que pour tout$ x $de$ I $,$ f(x) – g(x) = C $. On détermine la constante$ C $en calculant la valeur de$ f – g $pour une valeur particulière de$ x $dans$ I $ou en utilisant la limite lorsque$ x $tend vers l'une des bornes de$ I $. Exemple simplifier$ \quad \quad f(x) = \textrm{Arccos} \left ( 2 \, x \, \sqrt{1 – x^2} \right) $

Pour maximiser vos révisions à domicile, aidez-vous des autres cours en ligne et des exercices corrigés de l’ensemble des chapitres de maths pour les PTSI, PCSI et MPSI :