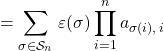Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours sur le Calcul des déterminants en MPSI, MP2I, PCSI et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
1. Cours sur le Groupe symétrique du déterminant en MPSI
1.1. Connaître les définitions sur le groupe Symétrique en MPSI
Définition 1 : On dit que ![]() est une permutation de
est une permutation de ![]() si
si ![]() est une bijection de
est une bijection de ![]() sur lui-même.
sur lui-même.
On peut noter ![]() .
.
- Propriété 1 : On note
 l’ensemble des permutations de
l’ensemble des permutations de ![Rendered by QuickLaTeX.com [\![1,\, n]\!]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2040%2018%22%3E%3C/svg%3E) .
.
 est un groupe appelé groupe symétrique d’ordre
est un groupe appelé groupe symétrique d’ordre  .
.
 .
.
Définition 2 : Le support d’une permutation ![]() est l’ensemble
est l’ensemble ![]() .
.
Dans la suite, il est noté ![]() .
.
Définition 3 : Deux permutations ![]() sont disjointes lorsque
sont disjointes lorsque ![]() .
.
- Propriété 2 : Si
 sont disjointes,
sont disjointes,  .
.
Définition 4 : ![]() est un cycle si
est un cycle si ![]() et
et ![]() éléments distincts de
éléments distincts de ![]() notés
notés ![]() tels que
tels que
![]()
![]() et
et ![]()
![]()
![]() ,
, ![]() .
.
On dit que ![]() est un cycle de longueur
est un cycle de longueur ![]() et
et ![]() est le support du cycle.
est le support du cycle.
On écrit ![]() .
.
mais aussi pour tout ![]() ,
,
![]() .
.
- Propriété 3 : Un cycle de longueur
 est d’ordre
est d’ordre  c’est -à-dire
c’est -à-dire ![Rendered by QuickLaTeX.com \sigma ^k = \textrm{Id}_{[[1,n]]}](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2093%2022%22%3E%3C/svg%3E) et si
et si ![Rendered by QuickLaTeX.com 1 \leq i \leq k - 1, \, \sigma^i \neq \textrm{Id}_{[[1,n]]}\,](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20203%2022%22%3E%3C/svg%3E) .
.
Définition 5 : Un cycle de longueur 2 est appelé transposition. Il existe donc deux éléments distincts ![]() et
et ![]() de
de ![]() tels que :
tels que : ![]()
et si ![]() .
.
On note ![]() .
.
1.2. Décomposition en produit de cycles
- Théorème 1 : Toute permutation de
![Rendered by QuickLaTeX.com [\![1,\, n]\!]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2040%2018%22%3E%3C/svg%3E) différente de
différente de  se décompose d’une et d’une seule façon en produit de cycles de supports disjoints à l’ordre près des facteurs.
se décompose d’une et d’une seule façon en produit de cycles de supports disjoints à l’ordre près des facteurs.
1.3. Décomposition en produit de transpositions
- Théorème 2 : Toute permutation est le produit de transpositions.
⚠️ : il n’y a pas unicité de la décomposition et les supports ne sont pas nécessairement disjoints - Propriété 4 :
 ,
,
 .
.
1.4.Signature en maths sup
- Théorème 3 : ll existe une unique application
 telle que
telle que  et telle que
et telle que  si
si  est une transposition.
est une transposition.
On dit que ![]() est la signature de
est la signature de ![]() .
.
![]() est paire (resp. impaire) si
est paire (resp. impaire) si ![]() (resp.
(resp. ![]() ).
).
- Théorème 4 : Si
![Rendered by QuickLaTeX.com \mathcal{P} = \{ \{i \, , j \} \in [\![1 , n]\!]^2 \, \setminus \, i \neq j \}](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20229%2020%22%3E%3C/svg%3E)
 .
. - Propriété 5 : La signature d’un cycle de longueur
 est égale à
est égale à  .
.
La signature de est égale à 1 (resp
est égale à 1 (resp  ) ssi
) ssi  est un produit d’un nombre pair (resp. impair) de transpositions.
est un produit d’un nombre pair (resp. impair) de transpositions. - Propriété 6 : On dit que le couple
 tel que
tel que  présente une inversion pour
présente une inversion pour  lorsque
lorsque  .
.
 est égal à
est égal à  où
où  est le nombre d’inversions de
est le nombre d’inversions de  .
.
2. Forme  linéaire alternée du déterminant en Maths Sup
linéaire alternée du déterminant en Maths Sup
Hypothèses : dans ce paragraphe, ![]() est le corps des réels ou le corps des complexes et
est le corps des réels ou le corps des complexes et ![]() ,
, ![]() .
.
Définition : Soit ![]() un
un ![]() – espace vectoriel ; on dit qu’une application
– espace vectoriel ; on dit qu’une application ![]() de
de ![]() à valeurs dans
à valeurs dans ![]() est
est
a) une forme ![]() – linéaire lorsque
– linéaire lorsque
![]() ,
, ![]() , l’application
, l’application
![]() ,
, ![]() est linéaire.
est linéaire.
Dans le cas ![]() , on dit que
, on dit que ![]() est une application bilinéaire, dans le cas
est une application bilinéaire, dans le cas ![]() , on dit que c’est une application trilinéaire.
, on dit que c’est une application trilinéaire.
b) une forme alternée lorsque ![]() ,
, ![]() pour
pour ![]() .
.
- Propriété 1 : Soit
 est une forme
est une forme  -linéaire sur
-linéaire sur  . Il y a équivalence entre
. Il y a équivalence entre

 est alternée
est alternée

 ,
,  est changé en son opposé si l’on échange deux vecteurs.
est changé en son opposé si l’on échange deux vecteurs.
On dit que est antisymétrique.
est antisymétrique.
 pour tout
pour tout 



- Propriété 2 : Si
 est une forme
est une forme  -linéaire alternée sur
-linéaire alternée sur  , la valeur
, la valeur  est inchangée si l’on ajoute à l’un des vecteurs une combinaison linéaire des autres.
est inchangée si l’on ajoute à l’un des vecteurs une combinaison linéaire des autres.
3. Déterminant dans une base en MPSI
Dans tout le paragraphe, ![]() est un
est un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() .
.
3.1. Définition d’un déterminant dans une base
- Théorème 1 : Soit
 une base de
une base de  . Il existe une unique forme
. Il existe une unique forme  linéaire alternée sur
linéaire alternée sur  qui est égale à 1 en
qui est égale à 1 en  .
.
On l’appelle déterminant dans la base et on la note
et on la note  .
. - Théorème 2 : Si
![Rendered by QuickLaTeX.com \forall\, j \in [\![1 , \, n]\!]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2085%2018%22%3E%3C/svg%3E) ,
, 


3.2.Propriétés des déteminants dans une base
![]() Propriétés du déterminant :
Propriétés du déterminant :
![]()
![]() est
est ![]() – linéaire.
– linéaire.
![]()
![]() si deux vecteurs sont égaux.
si deux vecteurs sont égaux.
![]()
![]() est changé en son opposé si l’on échange deux vecteurs.
est changé en son opposé si l’on échange deux vecteurs.
![]()
![]() est inchangé si l’on ajoute à l’un des vecteurs une combinaison linéaire des autres.
est inchangé si l’on ajoute à l’un des vecteurs une combinaison linéaire des autres.
![]() si
si ![]() ,
, ![]() ,
,
![]()
![]() .
.
![]()
![]() ssi
ssi ![]() est une base de
est une base de ![]() .
.
- Propriété : L’ensemble des formes
 linéaires alternées sur un
linéaires alternées sur un  -espace vectoriel de dimension
-espace vectoriel de dimension  est un espace vectoriel de dimension 1 engendré par
est un espace vectoriel de dimension 1 engendré par  .
. - Théorème : Changement de bases
Soit un
un  espace vectoriel de dimension
espace vectoriel de dimension  , soient
, soient  et
et  deux bases de
deux bases de  . Pour toute famille
. Pour toute famille 
de vecteurs de
vecteurs de  ,
,
 .
.
4. Déterminant d’un endomorphisme en MPSI, PCSI et PTSI
- Propriété 1 : Soit
 , il existe un unique réel appelé déterminant de
, il existe un unique réel appelé déterminant de  et noté
et noté  tel que pour toute famille
tel que pour toute famille 
de vecteurs de
vecteurs de  et pour toute base
et pour toute base  de
de  ,
,

en particulier .
. - Propriété 2 : Si
 ,
,


 si
si  .
. - Propriété 3 : Si
 ,
,  est un automorphisme de
est un automorphisme de  ssi
ssi  .
.
Et dans ce cas .
.
5. Déterminant d’une matrice carrée en maths sup
Soit ![]() .
.
Le déterminant de ![]() , noté
, noté ![]() , est égal à
, est égal à
![]()
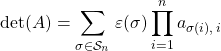
![]() au déterminant des vecteurs colonnes de
au déterminant des vecteurs colonnes de ![]() dans la base canonique de
dans la base canonique de ![]()
![]() au déterminant de l’endomorphisme
au déterminant de l’endomorphisme ![]() canoniquement associé à
canoniquement associé à ![]() .
.
![]() au déterminant de
au déterminant de ![]() si
si ![]() est la matrice de
est la matrice de ![]() dans une base
dans une base ![]() de
de ![]() .
.
- Propriété 1 :
 et
et  ont même déterminant.
ont même déterminant. - Propriété 2 : Si
 et
et  sont deux matrices carrées d’ordre
sont deux matrices carrées d’ordre  ,
,  .
.
Si ,
,  .
. - Propriété 3 :
 est inversible ssi
est inversible ssi  et dans ce cas,
et dans ce cas,  .
.
6. Développement suivant une colonne ou une ligne
Dans ce paragraphe, on note ![]() .
.
Définition : Soit ![]() . On appelle :
. On appelle :
![]() mineur de
mineur de ![]() en position
en position ![]() le déterminant de la matrice carrée
le déterminant de la matrice carrée ![]() d’ordre
d’ordre ![]() obtenue en supprimant la ligne
obtenue en supprimant la ligne ![]() et la colonne
et la colonne ![]() . On peut le noter
. On peut le noter ![]() .
.
![]() cofacteur de
cofacteur de ![]() en position
en position ![]() le scalaire
le scalaire ![]() .
.
![]() comatrice de
comatrice de ![]() , la matrice carrée d’ordre
, la matrice carrée d’ordre ![]()
![]() avec
avec ![]() .
.
![]() développement suivant la ligne
développement suivant la ligne ![]()
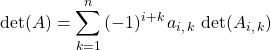
![]() développement suivant la colonne
développement suivant la colonne ![]()
UN PROF DE MATHS POUR EXCELLER
La pratique et la compréhension
clés de la réussite
Cours de maths en ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
7. Déterminant de matrices triangulaires par blocs
- Propriété 1 : On suppose que
 où
où  et
et  sont carrées.
sont carrées.
 .
. - Propriété 2 : On suppose que
 où
où  et
et  sont carrées.
sont carrées.
 .
. - Propriété 3 : Le déterminant d’une matrice triangulaire est égal au produit des termes diagonaux.
7.1. Déterminant de Vandermonde
La définition et la valeur sont au programme de MPSI, PCSI et PTSI.
7.1.1. Définition déterminant de Vandermonde
Soit ![]() ,
, ![]() .
.
Soit ![]() .
.
Le déterminant de Vandermonde associé à ces ![]() scalaires est noté
scalaires est noté ![]() et égal aux déterminants
et égal aux déterminants
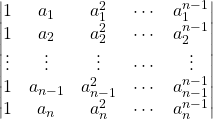 .
.
ou 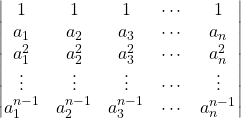 .
.
7.1.2. Valeur déterminant de Vandermonde
![]()
Première méthode de calcul : par introduction d’une fonction polynôme
On note si ![]() ,
, ![]()
![]()
![]() Pour
Pour ![]() ,
,
![]() .
.
Ce qui prouve ![]() .
.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
On introduit ![]() et
et ![]() en supposant
en supposant ![]() 2 à 2 distincts.
2 à 2 distincts.
![]()

On développe le déterminant suivant la dernière ligne
![]()
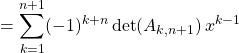 .
.
On obtient une fonction polynôme de degré ![]() et de coefficient dominant
et de coefficient dominant ![]()
![]() (ce qui justifie
(ce qui justifie ![]() ).
).
On remarque que ![]()
(il y a deux lignes identiques : la ligne ![]() et la ligne
et la ligne ![]() ).
).
Donc 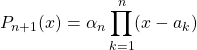
alors ![]()
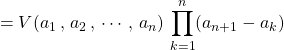

Le dernier produit est le facteur pour ![]() du premier produit,
du premier produit,
![]()
![]()
ce qui donne
![]()
![]() .
.
Le résultat reste valable si ![]() pour
pour ![]() , car il s’écrit
, car il s’écrit ![]() .
.
On a établi ![]() .
.
Deuxième méthode de calcul : par combinaison linéaire de toutes les lignes.
On raisonne aussi par récurrence, avec la même hypothèse de récurrence et cette fois-ci, on suppose ![]() et on cherche à exprimer
et on cherche à exprimer
![]()
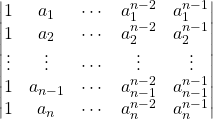
On introduit 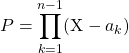 .
.
On développe ![]() sous la forme
sous la forme 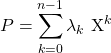 ,
,
on remarque que ![]() .
.
Puis on utilise l’opération 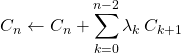
Le terme de la ligne ![]() et de la colonne
et de la colonne ![]() est égal à
est égal à  .
.
![]()
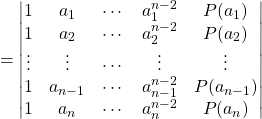
Donc la dernière colonne est formée de ![]() zéros suivis de
zéros suivis de ![]()
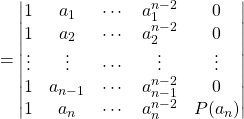
et en développant suivant la dernière colonne
![]() .
.
On termine par récurrence en utilisant ![]() et
et 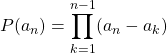 .
.
Troisième méthode : en retranchant à chaque colonne ![]() fois la colonne précédente en commençant par la fin.
fois la colonne précédente en commençant par la fin.
En effectuant les opérations : ![]()
![]()
![]() et
et ![]() ,
,
![]()
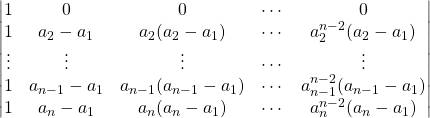
On développe suivant la première ligne
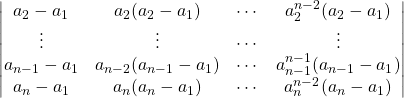
on factorise ![]() en ligne
en ligne ![]() pour tout
pour tout ![]() ,
,
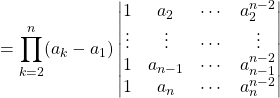
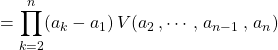
et on termine par récurrence.
7.2. Déterminant d’une matrice tri-diagonale
Soit ![]() une matrice carrée d’ordre
une matrice carrée d’ordre ![]() tri-diagonale, c’est à dire il existe trois scalaires
tri-diagonale, c’est à dire il existe trois scalaires ![]() tels que
tels que
![]()
![]() si
si ![]() ,
,
![]()
![]() si
si ![]()
![]()
![]() si
si ![]()
![]() les autres termes étant nuls.
les autres termes étant nuls.
En développant suivant la première colonne, on obtient une suite récurrente linéaire d’ordre 2.
Exemple de calcul du déterminant d’une matrice tri-diagonale
On note donc 
On développe suivant la première ligne


Le premier déterminant est ![]() .
.
On développe le deuxième déterminant suivant la première ligne et on obtient un déterminant d’ordre ![]() égal à
égal à ![]() .
.
Si ![]() ,
, ![]() .
.
C’est une suite récurrente linéaire d’ordre 2 avec ![]() et
et ![]() .
.
7.3. En utilisant le caractère  – linéaire alterné du déterminant
– linéaire alterné du déterminant
On peut utiliser cette méthode lorsque les différentes colonnes peuvent s’écrire sous la forme ![]() .
.
Déterminant de la matrice carrée ![]() d’ordre
d’ordre ![]() telle que
telle que ![]() et
et ![]() si
si ![]()
On note ![]() la base canonique de
la base canonique de ![]() ,
, ![]() et
et ![]() .
.
Alors ![]()
![]()
![]() .
.
On développe le déterminant par ![]() -linéarité en écrivant
-linéarité en écrivant
![]() le déterminant ne contenant aucun vecteur
le déterminant ne contenant aucun vecteur ![]()
![]() les déterminants contenant une et une seule fois le vecteur
les déterminants contenant une et une seule fois le vecteur ![]() .
.
![]() les autres déterminants contiennent au moins 2 fois le même vecteur
les autres déterminants contiennent au moins 2 fois le même vecteur ![]() , donc ils sont nuls
, donc ils sont nuls
soit
![]()
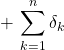
avec si ![]() ,
,
![]()
![]()
par ![]() -linéarité,
-linéarité,
![]()
avec ![]()
en retranchant au vecteur ![]() le vecteur
le vecteur ![]() , ce qui donne
, ce qui donne ![]() et ne change pas le déterminant
et ne change pas le déterminant ![]() :
:
![]()
![]()
![]() .
.
Donc 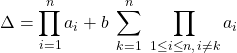 .
.
soit
![]()
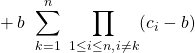 .
.
Lorsque ![]() , on peut écrire que :
, on peut écrire que :
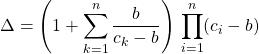 .
.
Simplifier le résultat lorsque ![]() .
.
![]()
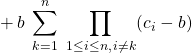 .
.
s’écrit
![]()
![]() .
.
7.4. Matrice du déterminant dont la somme des termes de chaque ligne est constante
Utiliser d’abord  , pour obtenir une première colonne de termes tous égaux à
, pour obtenir une première colonne de termes tous égaux à ![]() .
.
Puis effectuer des opérations du type ![]() pour obtenir
pour obtenir ![]() termes égaux à 0 en première colonne et développer suivant cette colonne.
termes égaux à 0 en première colonne et développer suivant cette colonne.
Exemple : Le déterminant de la matrice carrée d’ordre ![]() dont les termes de la diagonale sont égaux à
dont les termes de la diagonale sont égaux à ![]() et les termes non diagonaux sont égaux à
et les termes non diagonaux sont égaux à ![]() .
.
 .
.
Avec  ,
,
si l’on note ![]() ,
,

pour tout ![]() ,
, ![]() , on obtient
, on obtient
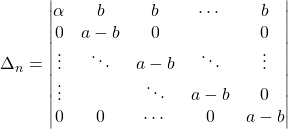
On obtient une matrice triangulaire supérieure, donc
![]()
soit ![]() .
.
On raisonnera de manière analogue lorsque la somme des termes de chaque colonne est constante.
7.5. En utilisant un déterminant par blocs en maths sup
Calcul de 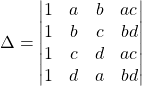
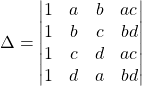
![]() et
et ![]()
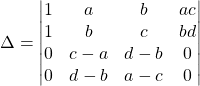
puis avec ![]()
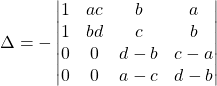
C’est le déterminant d’une matrice triangulaire par blocs
![]()
![]() .
.
Un cours avec des exercices beaucoup plus complet se trouve dans l’application mobile PrepApp que nous vous proposons gratuitement en téléchargement sur Google Play et Apple Store. Nous proposons de plus des cours de maths à domicile pour aider les étudiant à réussir en prépa.
Retrouvez d’autres cours en ligne :


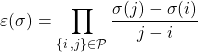 .
.