Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Ensembles et applications en Maths Sup MP2I, MPSI, PCSI, PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Ensembles et applications en Maths Sup
Plan :
1. Raisonnements sur les ensembles
2. Raisonnements sur les applications
3. Image directe et image réciproque
4. Relations d’équivalence et d’ordre
5. Lois internes
6. Structures
Ce chapitre fait partie des fondamentaux de l’année de maths sup. Les raisonnements et les propriétés qui seront travaillées en classe de MPSI, PCSI, PTSI ou encore de MP2I vous serviront durant les deux années de CPGE. Pour exceller, n’hésitez pas à faire appel à nos meilleurs professeurs de maths à domicile qui vous aideront à maitriser tous les éléments de ce chapitre.
1. Raisonnements sur les ensembles en MPSI, MP2I, PCSI, PTSI
1.1. Égalité et inclusion
![]() Pour démontrer que l’ensemble
Pour démontrer que l’ensemble ![]() est inclus dans l’ensemble
est inclus dans l’ensemble ![]() , on démontre que tout élément de
, on démontre que tout élément de ![]() est élément de
est élément de ![]() .
.
Il faut prendre le bon départ :
Si la propriété ![]() est vraie, pour démontrer que
est vraie, pour démontrer que ![]() , on part de
, on part de ![]() , pour arriver à
, pour arriver à ![]() , en utilisant dans la démonstration la propriété
, en utilisant dans la démonstration la propriété ![]() .
.
Un raisonnement consistant à traduire l’hypothèse ![]() ne permet pas de prendre le bon départ, donc ne permet pas de prouver l’inclusion attendue.
ne permet pas de prendre le bon départ, donc ne permet pas de prouver l’inclusion attendue.
exemple : Soient ![]() trois parties de
trois parties de ![]() . Démontrer que
. Démontrer que ![]() .
.
Correction : Il faut s’assurer de prendre le bon départ : on cherche à prouver une inclusion.
On part donc de : ![]() ,
,
![]() lorsque
lorsque ![]() ,
, ![]() car
car ![]()
![]() lorsque
lorsque ![]() ,
, ![]() car
car ![]() donc
donc ![]() .
.
Dans les deux cas, ![]() .
.
On a donc prouvé que ![]() .
.
![]() Pour démontrer que l’ensemble
Pour démontrer que l’ensemble ![]() n’est pas inclus dans l’ensemble
n’est pas inclus dans l’ensemble ![]() , on cherche un élément de
, on cherche un élément de ![]() qui n’est pas élément de
qui n’est pas élément de ![]() .
.
![]() Pour utiliser le fait que
Pour utiliser le fait que ![]() n’est pas inclus dans
n’est pas inclus dans ![]() , on introduit
, on introduit ![]() tel que
tel que ![]() .
.
![]() Il est parfois possible de démontrer l’inclusion
Il est parfois possible de démontrer l’inclusion ![]() en raisonnant directement sur les ensembles et en utilisant les propriétés de l’intersection et de la réunion.
en raisonnant directement sur les ensembles et en utilisant les propriétés de l’intersection et de la réunion.
exemple : Soient ![]() trois parties de
trois parties de ![]() . Démontrer que
. Démontrer que ![]() .
.
Correction : On utilise la suite d’inclusions ![]()
pour démontrer que ![]() .
.
Si l’on veut raisonner avec les éléments, on part de ![]() .
.
Alors ![]() , donc
, donc ![]() et en particulier
et en particulier ![]() .
.
On a prouvé que tout élément ![]() de
de ![]() est élément de
est élément de ![]() , donc prouvé que
, donc prouvé que ![]() .
.
![]() Pour démontrer que les ensembles
Pour démontrer que les ensembles ![]() et
et ![]() sont égaux, il suffit de prouver que
sont égaux, il suffit de prouver que ![]() et que
et que ![]() .
.
![]() Pour démontrer que les ensembles E et
Pour démontrer que les ensembles E et ![]() sont différents, il suffit de trouver un élément
sont différents, il suffit de trouver un élément ![]() de
de ![]() qui n’est pas dans
qui n’est pas dans ![]() ou de trouver un élément
ou de trouver un élément ![]() de
de ![]() qui n’est pas dans
qui n’est pas dans ![]() .
.
![]() Il est parfois possible de démontrer l’égalité
Il est parfois possible de démontrer l’égalité ![]() en raisonnant directement sur les ensembles et en utilisant les propriétés des lois intersection et réunion.
en raisonnant directement sur les ensembles et en utilisant les propriétés des lois intersection et réunion.
exemple : Soient ![]() quatre parties de
quatre parties de ![]() . Si
. Si ![]() ,
, ![]() et
et ![]() ,
,
on peut établir directement que ![]() .
.
Correction : On suppose que ![]() et
et ![]() où
où ![]() .
.
![]()
![]()
En utilisant les hypothèses :
![]()
A ne pas confondre les différentes notations.
Si ![]() est un ensemble, si
est un ensemble, si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() et
et ![]() un élément de
un élément de ![]() , on écrit :
, on écrit :
![]()
![]() ou
ou ![]()
![]()
![]() ou
ou ![]()
![]()
![]() mais
mais ![]()
![]() si
si ![]() est inclus dans
est inclus dans ![]() ,
, ![]() ou
ou ![]() .
.
Bien distinguer « ![]() » de «
» de « ![]() « .
« .
1.2. Complémentaires
Définition :
Si ![]() est une partie de
est une partie de ![]() , le complémentaire de
, le complémentaire de ![]()
![]()
est l’ensemble des éléments de ![]() qui ne sont pas dans
qui ne sont pas dans ![]() .
.
Manipuler correctement les complémentaires :
![]()
![]() et
et ![]()
![]() Si
Si ![]() ,
, ![]()
![]() Si
Si ![]() et
et ![]() ,
,
![]() et
et ![]() .
.
![]() Pour toute famille non vide
Pour toute famille non vide ![]() de parties de
de parties de ![]() .
.
![]() et
et ![]() .
.
Une formule utile :
Si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() ,
, ![]() .
.
Elle découle de ![]() .
.
1.3. Propriétés de la réunion et l’intersection (PCSI)
Soit ![]() un ensemble.
un ensemble.
Si ![]() sont trois parties de
sont trois parties de ![]() ,
,
![]() Associativité :
Associativité :
![]()
![]() .
.
![]()
![]() .
.
![]() Commutativité
Commutativité
![]()
![]() .
.
![]()
![]() .
.
![]() Avec
Avec ![]() et
et ![]() ,
,
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]() Distributivité
Distributivité
![]() de l’intersection par rapport à la réunion
de l’intersection par rapport à la réunion
![]() .
.
![]() de la réunion par rapport à l’intersection
de la réunion par rapport à l’intersection
![]() .
.
1.4. Réunion et intersection d’une famille quelconque
Soit ![]() un ensemble et
un ensemble et ![]() un ensemble non vide.
un ensemble non vide.
On suppose que ![]() .
.
Soit ![]() .
.
![]() ssi
ssi ![]()
![]() ssi
ssi ![]() .
.
Dans la suite, on garde les mêmes notations.
Propriétés
![]() si
si ![]()
![]()
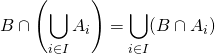
![]()
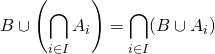
![]() Lois de Morgan
Lois de Morgan
![]()
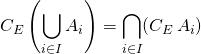
![]()

COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Raisonnements sur les applications en prepa maths sup
2.1. Les définitions
![]() Connaître les différentes notations
Connaître les différentes notations
Si ![]() et
et ![]() sont deux ensembles non vides,
sont deux ensembles non vides,
![]()
![]() est l’ensemble des applications de
est l’ensemble des applications de ![]() dans
dans ![]() .
.
![]()
![]() est l’élément de
est l’élément de ![]() défini par
défini par ![]() .
.
![]() Si
Si ![]() , l’indicatrice de
, l’indicatrice de ![]() est l’application notée
est l’application notée ![]() définie par
définie par ![]() .
.
👍 Si ![]() et
et ![]() sont deux parties de
sont deux parties de ![]() ,
,
![]()
![]() ssi
ssi ![]()
![]()
![]() ssi
ssi ![]() .
.
On peut donc utiliser les fonctions indicatrices pour démontrer l’égalité ou l’inclusion de deux ensembles.
![]() Si
Si ![]() est une partie de
est une partie de ![]() et
et ![]() , la restriction de
, la restriction de ![]() à
à ![]() est
est
![]() ,
, ![]() .
.
![]() Si
Si ![]() est une partie de
est une partie de ![]() , on appelle prolongement de
, on appelle prolongement de ![]() à
à ![]() toute application
toute application ![]() telle que la restriction de
telle que la restriction de ![]() à
à ![]() soit égale à
soit égale à ![]() .
.
![]() Soient
Soient ![]() et
et ![]() une partie de
une partie de ![]() ,
,
![]()
![]() est stable par
est stable par ![]()
![]() ssi
ssi ![]()
![]() ssi
ssi ![]() .
.
![]() Si
Si ![]() est stable par
est stable par ![]() , on peut définir l’application induite par
, on peut définir l’application induite par ![]() sur
sur ![]() :
: ![]() .
.
![]() Composition
Composition
![]() Soient
Soient ![]() ,
, ![]() et
et ![]() 3 ensembles non vides, si
3 ensembles non vides, si ![]() et
et ![]() , on peut définir
, on peut définir ![]()
par ![]()
⚠️ Toujours vérifier que la composition a un sens.
Si ![]() , on peut toujours définir
, on peut toujours définir ![]() et
et ![]() .
.
![]() Si
Si ![]() ,
, ![]() ,
, ![]() et
et ![]() sont quatre ensembles non vides, si
sont quatre ensembles non vides, si ![]() ,
, ![]() et
et ![]() ,
, ![]()
Cette application est notée ![]() .
.
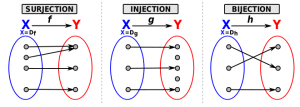
2.2. Injection
Dans ce paragraphe, ![]() est une application de
est une application de ![]() dans
dans ![]() .
.
![]() pour démontrer que
pour démontrer que ![]() est une injection, on démontre que si
est une injection, on démontre que si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() tels que
tels que ![]() , alors
, alors ![]() .
.
![]() pour démontrer que
pour démontrer que ![]() est une injection, il suffit de montrer que
est une injection, il suffit de montrer que ![]() est la composée de deux injections.
est la composée de deux injections.
![]() pour démontrer que
pour démontrer que ![]() n’est pas injective, on cherche
n’est pas injective, on cherche ![]() dans
dans ![]() tels que
tels que ![]() .
.
⚠️ : pour démontrer que sous l’hypothèse ![]() , l’application
, l’application ![]() définie sur
définie sur ![]() est injective, il faut prendre le bon départ :
est injective, il faut prendre le bon départ :
On part de ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() et on obtient (en utilisant
et on obtient (en utilisant ![]() au cours du raisonnement) que
au cours du raisonnement) que ![]() .
.
exercice : Soit ![]() .
.
S’il existe ![]() tel que
tel que ![]() est injective,
est injective, ![]() est injective.
est injective.
Correction : Soit ![]() tel que
tel que ![]() , ce sont deux éléments de
, ce sont deux éléments de ![]() .
.
On prend l’image par ![]() :
: ![]()
![]() soit
soit ![]() ,
,
comme ![]() est injective,
est injective, ![]() .
.
On a prouvé que ![]() est injective.
est injective.
2.3. Surjection
Dans ce paragraphe, ![]() est une application de
est une application de ![]() dans
dans ![]() .
.
![]() pour démontrer que
pour démontrer que ![]() est une surjection de
est une surjection de ![]() sur
sur ![]() , on démontre que pour tout élément
, on démontre que pour tout élément ![]() de
de ![]() , on peut trouver
, on peut trouver ![]() dans
dans ![]() tel que
tel que ![]() .
.
Ce qui revient à prouver que ![]() .
.
![]() Pour démontrer que
Pour démontrer que ![]() est surjective, il suffit de montrer que
est surjective, il suffit de montrer que ![]() est la composée de deux surjections.
est la composée de deux surjections.
![]() Pour prouver que
Pour prouver que ![]() n’est pas surjective, on trouve
n’est pas surjective, on trouve ![]() tel que pour tout
tel que pour tout ![]() ,
, ![]() .
.
⚠️ : pour démontrer que sous l’hypothèse ![]() , l’application
, l’application ![]() définie sur
définie sur ![]() à valeurs dans
à valeurs dans ![]() est surjective, il faut prendre le bon départ :
est surjective, il faut prendre le bon départ :
On part de ![]() et il faut trouver
et il faut trouver ![]() (en utilisant
(en utilisant ![]() au cours du raisonnement) tel que
au cours du raisonnement) tel que ![]() .
.
Exercice : Soit ![]() .
.
S’il existe ![]() tel que
tel que ![]() est surjective,
est surjective, ![]() est surjective.
est surjective.
Correction : L’application ![]() est définie et
est définie et ![]() .
.
Soit ![]() , comme
, comme ![]() est surjective, il existe
est surjective, il existe ![]() tel que
tel que ![]() ,
,
on écrit donc ![]() où
où ![]() .
.
On a prouvé que ![]() est une surjection de
est une surjection de ![]() sur
sur ![]() .
.
2.4. Bijection
Dans le paragraphe, ![]() est une application de
est une application de ![]() dans
dans ![]() .
.
![]() Il y a équivalence entre
Il y a équivalence entre
![]()
![]() est une bijection de
est une bijection de ![]() sur
sur ![]()
![]()
![]() est injective et surjective
est injective et surjective
![]() pour tout
pour tout ![]() de
de ![]() , il existe un et un seul
, il existe un et un seul ![]() de
de ![]() tel que
tel que ![]()
![]() il existe
il existe ![]() tel que
tel que ![]() et
et ![]()
( alors ![]() ).
).
![]() Dans le cas où
Dans le cas où ![]() est une fonction définie dans un intervalle
est une fonction définie dans un intervalle ![]() de
de ![]() à valeurs dans
à valeurs dans ![]() , on peut chercher à démontrer que
, on peut chercher à démontrer que ![]() est continue sur
est continue sur ![]() , strictement monotone sur
, strictement monotone sur ![]() et que
et que ![]() . Alors
. Alors ![]() est une bijection de
est une bijection de ![]() sur
sur ![]() .
.
Dans ce cas les graphes de ![]() et de
et de ![]() sont symétriques par rapport à la droite d’équation
sont symétriques par rapport à la droite d’équation ![]() .
.
![]() Si
Si ![]() vérifie
vérifie ![]() , alors
, alors ![]() est une bijection et
est une bijection et ![]() .
.
![]() Lorsque
Lorsque ![]() est une bijection de
est une bijection de ![]() sur
sur ![]() , pour déterminer
, pour déterminer ![]() :
:
![]() on peut résoudre l’équation :
on peut résoudre l’équation : ![]() et
et ![]() ,
, ![]() , alors
, alors
![]() .
.
![]() on peut déterminer une fonction
on peut déterminer une fonction ![]() de
de ![]() dans
dans ![]() telle que
telle que ![]() ou telle que
ou telle que ![]() , alors
, alors ![]() .
.
![]() Si
Si ![]() est une composée de deux bijections,
est une composée de deux bijections, ![]() est bijective.
est bijective.
![]() ⚠️ si
⚠️ si ![]() et
et ![]() , lorsque
, lorsque ![]() et
et ![]() sont des bijections,
sont des bijections, ![]() est une bijection de
est une bijection de ![]() sur
sur ![]() et
et ![]()
Un petit dessin pour illustrer.
COURS DE MATHS A DOMICILE
Les meilleurs profs de maths pour
réussir sa scolarité
En ligne ou à domicile
Avis Google France ★★★★★ 4,9 sur 5
3. Image directe et image réciproque
3.1. Les définitions
Soient ![]() ,
, ![]() une partie de
une partie de ![]() et
et ![]() une partie de
une partie de ![]() .
.
![]() Connaître les définitions :
Connaître les définitions :
![]() l’image directe de
l’image directe de ![]() par
par ![]() :
:
![]()
c’est une partie de ![]() .
.
![]() l’image réciproque de
l’image réciproque de ![]() par
par ![]() :
:
![]()
c’est une partie de ![]() .
.
![]() Savoir les traduire :
Savoir les traduire :
![]()
![]() ssi
ssi ![]()
![]()
![]() ssi
ssi ![]() .
.
⚠️ : Si ![]() est une partie de
est une partie de ![]() , on peut définir
, on peut définir ![]() même si
même si ![]() n’est pas bijective.
n’est pas bijective.
Lorsque ![]() est bijective,
est bijective, ![]() est aussi l’image directe de
est aussi l’image directe de ![]() par l’application réciproque
par l’application réciproque ![]() .
.
On peut définir pour tout ![]() ,
, ![]() qui est une partie de
qui est une partie de ![]() , mais pour définir
, mais pour définir ![]() , l’application
, l’application ![]() doit être bijective et dans ce cas,
doit être bijective et dans ce cas, ![]() est un élément de
est un élément de ![]() .
.
⚠️ Il faudra faire attention :
![]() Lorsque
Lorsque ![]() est élément de
est élément de ![]() ,
, ![]() est un élément de
est un élément de ![]() et
et ![]() est une partie de
est une partie de ![]() .
.
![]() Lorsque
Lorsque ![]() est une partie de
est une partie de ![]() ,
, ![]() est une partie de
est une partie de ![]() .
.
![]() Lorsque
Lorsque ![]() est une partie de
est une partie de ![]() ,
, ![]() est une partie de
est une partie de ![]() .
.
Deux images pour illustrer (image directe puis image réciproque)
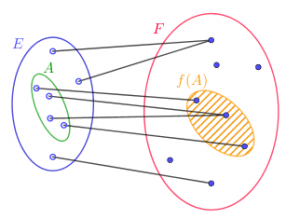
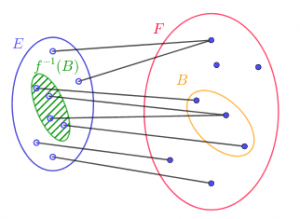
3.2. Les propriétés
Soit ![]() une application de
une application de ![]() dans
dans ![]() .
.
![]()
![]() est une surjection de
est une surjection de ![]() sur
sur ![]() ssi
ssi ![]() .
.
![]() Vous pouvez utiliser les évidences :
Vous pouvez utiliser les évidences :
![]()
![]()
![]() .
.
![]()
![]()
![]() .
.
Dans la suite, les propriétés énoncées ne sont pas explicitement au programme mais seront démontrées dans une des autres tâches.
![]() les propriétés de l’image directe
les propriétés de l’image directe
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
⚠️ inclusion seulement dans le cas général : prendre ![]() ,
, ![]() et
et ![]() ,
, ![]() et
et ![]() .
.
![]() les propriétés de l’image réciproque
les propriétés de l’image réciproque
Si ![]() et
et ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() les propriétés combinées
les propriétés combinées
![]() Si
Si ![]() ,
, ![]()
![]() Si
Si ![]() ,
, ![]() .
.
⚠️ en général ce ne sont que des inclusions
Démonstration : ![]() Première propriété
Première propriété
![]() Si
Si ![]() ,
,
pour tout ![]() ,
, ![]() donc par définition de l’image réciproque,
donc par définition de l’image réciproque, ![]() .
.
On a prouvé que ![]() .
.
![]() un exemple d’inclusion stricte.
un exemple d’inclusion stricte.
Prendre ![]()
![]() ,
, ![]() et
et ![]() .
.
![]() Deuxième propriété
Deuxième propriété
![]() Si
Si ![]() ,
,
pour tout ![]() , il existe
, il existe ![]() tel que
tel que ![]() et par définition de l’image réciproque,
et par définition de l’image réciproque, ![]() soit
soit ![]() .
.
On a prouvé que ![]() .
.
![]() un exemple d’inclusion stricte.
un exemple d’inclusion stricte.
Prendre ![]()
![]() ,
, ![]() et
et ![]()
4. Relation d’équivalence et relation d’ordre
4.1. Relation binaire
Soit ![]() un ensemble
un ensemble
![]() Se donner une relation binaire
Se donner une relation binaire ![]() sur
sur ![]() revient à se donner une partie
revient à se donner une partie ![]() de
de ![]() et on écrit alors
et on écrit alors ![]() .
.
![]() Soit
Soit ![]() une relation binaire sur l’ensemble
une relation binaire sur l’ensemble ![]() .
.
![]()
![]() est réflexive si
est réflexive si ![]()
![]()
![]() est symétrique si
est symétrique si ![]()
![]()
![]() est antisymétrique si
est antisymétrique si ![]() et
et ![]()
![]()
![]() est transitive si
est transitive si ![]()
![]() et
et ![]()
4.2. Définitions
Soit ![]() un ensemble.
un ensemble.
![]() Une relation binaire
Une relation binaire ![]() sur
sur ![]() est une relation d’équivalence lorsqu’elle est réflexive, symétrique et transitive.
est une relation d’équivalence lorsqu’elle est réflexive, symétrique et transitive.
exemples :
![]() Sur tout ensemble
Sur tout ensemble ![]() , »
, » ![]() » définit une relation d’équivalence.
» définit une relation d’équivalence.
![]() Sur l’ensemble
Sur l’ensemble ![]() des droites du plan
des droites du plan ![]() la relation »
la relation » ![]() est parallèle à
est parallèle à ![]() » définit une relation d’équivalence.
» définit une relation d’équivalence.
![]() Si
Si ![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() et
et ![]() ,
,
la classe d’équivalence de ![]() suivant
suivant ![]() est la partie de
est la partie de ![]() définie par
définie par
![]()
elle peut aussi être notée ![]() ou
ou ![]() .
.
![]()
![]()
![]() si
si ![]() ,
, ![]() ou
ou ![]() .
.
![]()
![]() .
.
L’ensemble des classes d’équivalence forme une partition de ![]() .
.
4.3.Congruence
![]() Si
Si ![]() , on définit si
, on définit si ![]() ,
,
![]()
C’est une relation d’équivalence sur ![]() appelée relation de congruence modulo
appelée relation de congruence modulo ![]() (cas usuel en trigonométrie :
(cas usuel en trigonométrie : ![]() ou
ou ![]() ).
).
![]() Si
Si ![]() , on définit si
, on définit si ![]() ,
,
![]()
C’est une relation d’équivalence sur ![]() appelée relation de congruence modulo
appelée relation de congruence modulo ![]() .
.
Pour la relation de congruence modulo ![]() , il y a
, il y a ![]() classes d’équivalence définies pour
classes d’équivalence définies pour ![]() par
par ![]() .
.
Exercice
La relation de congruence modulo ![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() vérifiant
vérifiant
si ![]() et
et ![]() ,
,
![]() et
et ![]() .
.
Correction :
![]() Relation d’équivalence
Relation d’équivalence
![]() Pour tout
Pour tout ![]() donc
donc ![]() .
.
![]() Si
Si ![]() vérifie
vérifie ![]()
![]() donc
donc ![]() avec
avec![]() , donc
, donc ![]() .
.
![]() Si
Si ![]() vérifie
vérifie ![]() et
et ![]() .
.
![]() et
et ![]() , donc
, donc ![]() avec
avec ![]() , donc
, donc ![]() .
.
On a démontré que la relation de congruence modulo ![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() .
.
![]() Classes d’équivalence.
Classes d’équivalence.
![]() On suppose que
On suppose que ![]() , alors
, alors ![]() et
et ![]() ne sont pas congrus modulo
ne sont pas congrus modulo ![]() .
.
En effet ![]() n’est pas divisible par
n’est pas divisible par ![]() , alors
, alors ![]() . Il y a donc au moins
. Il y a donc au moins ![]() classes d’équivalence.
classes d’équivalence.
![]()
![]() ssi
ssi ![]() est un multiple de
est un multiple de ![]() , donc
, donc ![]() .
.
![]() Pour tout
Pour tout ![]() , par division euclidienne, on écrit
, par division euclidienne, on écrit ![]() avec
avec ![]() et
et ![]() , donc
, donc ![]() et
et ![]() .
.
Pour la relation de congruence modulo ![]() , il y a
, il y a ![]() classes d’équivalence
classes d’équivalence
si ![]() ,
, ![]()
![]() Opérations sur les congruences.
Opérations sur les congruences.
On suppose que ![]() et
et ![]()
![]() tel que
tel que ![]() et
et ![]() .
.
![]() Par somme,
Par somme, ![]() avec
avec ![]() donc
donc ![]() .
.
![]() Par produit,
Par produit,
![]() avec
avec ![]() , donc
, donc ![]() .
.
4.4. Relation d’ordre
Soit ![]() un ensemble non vide.
un ensemble non vide.
![]() Une relation binaire sur
Une relation binaire sur ![]() est une relation d’ordre lorsqu’elle est réflexive, antisymétrique et transitive.
est une relation d’ordre lorsqu’elle est réflexive, antisymétrique et transitive.
On la note souvent ![]() .
.
On dit alors que l’ensemble ![]() est un ensemble ordonné.
est un ensemble ordonné.
![]() La relation d’ordre
La relation d’ordre ![]() sur
sur ![]() est une relation d’ordre total lorsque pour tout
est une relation d’ordre total lorsque pour tout ![]() , au moins une des deux relations
, au moins une des deux relations ![]() ou
ou ![]() est vérifiée.
est vérifiée.
On dit alors que ![]() est un ensemble totalement ordonné.
est un ensemble totalement ordonné.
![]() La relation d’ordre
La relation d’ordre ![]() sur
sur ![]() est une relation d’ordre partiel lorsqu’ il existe
est une relation d’ordre partiel lorsqu’ il existe ![]() tel que les relations
tel que les relations ![]() et
et ![]() soient fausses.
soient fausses.
On dit alors que ![]() est un ensemble partiellement ordonné.
est un ensemble partiellement ordonné.
exemples
![]() sur
sur ![]() , la relation
, la relation ![]() définit une relation d’ordre total.
définit une relation d’ordre total.
![]() Si
Si ![]() est un ensemble contenant au moins deux éléments, la relation
est un ensemble contenant au moins deux éléments, la relation ![]() définit une relation d’ordre partiel sur
définit une relation d’ordre partiel sur ![]() .
.
![]() Si
Si ![]() est une partie contenant au moins deux éléments, la relation définie sur
est une partie contenant au moins deux éléments, la relation définie sur ![]() par
par
![]()
est une relation d’ordre partiel.
5. Loi interne
![]() Définir une loi de composition interne sur un ensemble
Définir une loi de composition interne sur un ensemble ![]() revient à se donner une application
revient à se donner une application ![]() .
.
Si ![]() , on note souvent
, on note souvent ![]() ou
ou ![]() ou
ou ![]() etc …
etc …
exemples :
![]() Sur
Sur ![]() , l’intersection, la réunion.
, l’intersection, la réunion.
![]() Sur
Sur ![]() , l’addition définie si
, l’addition définie si ![]() par
par ![]() .
.
![]() Sur
Sur ![]() , la loi
, la loi ![]() .
.
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() est associative, on démontre que
est associative, on démontre que ![]()
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() n’est pas associative, on trouve trois éléments
n’est pas associative, on trouve trois éléments ![]() et
et ![]() de
de ![]() tels que
tels que ![]() .
.
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() est commutative, on démontre que
est commutative, on démontre que ![]() .
.
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() n’est pas commutative, on trouve deux éléments
n’est pas commutative, on trouve deux éléments ![]() et
et ![]() de
de ![]() tels que
tels que ![]() .
.
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() est distributive par rapport à la loi
est distributive par rapport à la loi ![]() , on démontre que
, on démontre que ![]()
![]()
![]() et
et ![]() .
.
👍 la deuxième égalité étant inutile si la loi ![]() est commutative.
est commutative.
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() n’est pas distributive par rapport à la loi
n’est pas distributive par rapport à la loi ![]() , on trouve trois éléments
, on trouve trois éléments ![]() et
et ![]() de
de ![]() tels que
tels que
![]()
ou ![]() .
.
![]() Pour démontrer qu’une loi de composition interne
Pour démontrer qu’une loi de composition interne ![]() définie sur
définie sur ![]() admet un élément neutre :
admet un élément neutre :
a) si l’on a l’intuition de la valeur de l’élément neutre ![]() , on vérifie que l’on a bien
, on vérifie que l’on a bien ![]() .
.
👍 La démonstration de ![]() suffit dans le cas d’une loi commutative.
suffit dans le cas d’une loi commutative.
b) sinon, on écrit que ![]() ,
,
pour chercher à déterminer ![]() .
.
Si le raisonnement n’a pas été fait par équivalence, après avoir trouvé ![]() , il faut vérifier que pour tout
, il faut vérifier que pour tout ![]() de
de ![]() ,
,
![]() .
.
👍 La recherche de ![]() peut se faire uniquement au brouillon, et dans un devoir on peut se limiter au raisonnement décrit en a).
peut se faire uniquement au brouillon, et dans un devoir on peut se limiter au raisonnement décrit en a).
![]() Pour démontrer qu’un élément
Pour démontrer qu’un élément ![]() admet un symétrique pour la loi de composition interne
admet un symétrique pour la loi de composition interne ![]() d’élément neutre e,
d’élément neutre e,
a) si l’on a l’intuition de la valeur du symétrique ![]() de
de ![]() : on vérifie que l’on a bien
: on vérifie que l’on a bien ![]() .
.
👍 La démonstration de l »égalité ![]() suffit dans le cas d’une loi commutative.
suffit dans le cas d’une loi commutative.
b) sinon, on écrit que ![]()
pour chercher à déterminer ![]() .
.
Si le raisonnement n’a pas été fait par équivalence, après avoir trouvé ![]() , il faut vérifier que
, il faut vérifier que ![]() .
.
👍 La recherche de ![]() peut se faire uniquement au brouillon, et dans un devoir, on peut se limiter au raisonnement décrit en a).
peut se faire uniquement au brouillon, et dans un devoir, on peut se limiter au raisonnement décrit en a).
![]() Pour démontrer que la partie
Pour démontrer que la partie ![]() de
de ![]() est une partie stable pour la loi de composition interne
est une partie stable pour la loi de composition interne ![]() définie sur
définie sur ![]() , on doit prouver que pour tous
, on doit prouver que pour tous ![]() et
et ![]() de
de ![]() ,
, ![]() est élément de
est élément de ![]() .
.
![]() Pour prouver que
Pour prouver que ![]() n’est pas une partie stable pour la loi
n’est pas une partie stable pour la loi ![]() , on doit trouver
, on doit trouver ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() ne soit pas élément de
ne soit pas élément de ![]() .
.
Propriétés
Si la loi interne ![]() est associative,
est associative,
![]() si l’élément neutre existe, il est unique
si l’élément neutre existe, il est unique
![]() si la loi
si la loi ![]() possède un élément neutre, le symétrique de
possède un élément neutre, le symétrique de ![]() lorsqu’il existe est unique.
lorsqu’il existe est unique.
On suppose dans la suite que la loi est associative.
Quand la loi est notée additivement, si la loi possède un élément neutre, il est noté ![]() et le symétrique de
et le symétrique de ![]() , s’il existe, est noté
, s’il existe, est noté ![]() et appelé opposé de
et appelé opposé de ![]() .
.
Quand la loi est notée multiplicativement, si la loi possède un élément neutre, il est noté ![]() et le symétrique de
et le symétrique de ![]() , s’il existe, est noté
, s’il existe, est noté ![]() et appelé inverse de
et appelé inverse de ![]() .
.
prop Soit ![]() un ensemble muni d’une loi interne associative notée multiplicativement.
un ensemble muni d’une loi interne associative notée multiplicativement.
Si ![]() et
et ![]() possèdent un inverse,
possèdent un inverse, ![]() possède un inverse et
possède un inverse et ![]() .
.
Exemple :
Soit ![]() un ensemble contenant au moins deux éléments. Quelles sont les propriétés des lois internes «
un ensemble contenant au moins deux éléments. Quelles sont les propriétés des lois internes « ![]() » et «
» et « ![]() » dans
» dans ![]() ?
?
Correction : ![]() Propriétés de la réunion :
Propriétés de la réunion :
![]() La réunion est associative et commutative.
La réunion est associative et commutative.
![]()
![]() est élément neutre pour la loi
est élément neutre pour la loi ![]()
car pour tout ![]() .
.
![]() Seul
Seul ![]() a un symétrique pour la loi
a un symétrique pour la loi ![]()
Car si ![]() , pour tout
, pour tout ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() Propriétés de l’intersection :
Propriétés de l’intersection :
![]() L’intersection est associative et commutative.
L’intersection est associative et commutative.
![]()
![]() est élément neutre pour la loi
est élément neutre pour la loi ![]()
car pour tout ![]() .
.
![]() Seul
Seul ![]() a un symétrique pour la loi
a un symétrique pour la loi ![]()
Car si ![]() , pour tout
, pour tout ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() Propriétés conjointes :
Propriétés conjointes :
![]() La réunion est distributive par rapport à l’intersection :
La réunion est distributive par rapport à l’intersection :
si ![]()
![]() .
.
![]() L’intersection est distributive par rapport à la réunion :
L’intersection est distributive par rapport à la réunion :
si ![]()
![]() .
.
6. Structures
6.1. Groupe
![]() Soit
Soit ![]() un ensemble non vide muni d’une loi interne notée
un ensemble non vide muni d’une loi interne notée ![]() .
.
On dit que ![]() est un groupe si, et seulement si,
est un groupe si, et seulement si,
![]() la loi
la loi ![]() est associative
est associative
![]() la loi
la loi ![]() possède un élément neutre noté
possède un élément neutre noté ![]()
![]() tout élément
tout élément ![]() de
de ![]() possède un symétrique noté
possède un symétrique noté ![]() .
.
Si, de plus, la loi ![]() est commutative, le groupe est dit commutatif.
est commutative, le groupe est dit commutatif.
![]() exemples :
exemples :
![]() Si
Si ![]() est un ensemble non vide, l’ensemble des bijections de
est un ensemble non vide, l’ensemble des bijections de ![]() sur
sur ![]() est un groupe pour la loi
est un groupe pour la loi ![]() , appelé groupe des permutations de
, appelé groupe des permutations de ![]() et noté
et noté ![]() .
.
![]()
![]() est un groupe commutatif
est un groupe commutatif
![]()
![]() est un groupe commutatif.
est un groupe commutatif.
![]() notations :
notations :
Si ![]() est un groupe d’élément neutre
est un groupe d’élément neutre ![]() et
et ![]() , on définit
, on définit
![]()
![]()
![]() et si
et si ![]()
![]() si
si ![]() .
.
Si ![]() est un groupe d’élément neutre
est un groupe d’élément neutre ![]() et
et ![]() , on définit
, on définit
![]()
![]() et si
et si ![]()
![]() si
si ![]() .
.
exercice :
Si ![]() est une loi de composition interne sur
est une loi de composition interne sur ![]() , associative et admettant un élément neutre
, associative et admettant un élément neutre ![]() , l’ensemble
, l’ensemble ![]() des éléments inversibles de
des éléments inversibles de ![]() est un groupe pour la multiplication.
est un groupe pour la multiplication.
Démonstration : ![]()
![]() est non vide car
est non vide car ![]() est inversible, d’inverse égal à lui même.
est inversible, d’inverse égal à lui même.
![]() Si
Si ![]() , on a vu que
, on a vu que ![]() est inversible.
est inversible.
Donc la loi ![]() est une loi interne dans
est une loi interne dans ![]() .
.
![]() La multiplication est associative dans
La multiplication est associative dans ![]() car elle l’est dans
car elle l’est dans ![]() .
.
![]()
![]() est encore élément neutre dans
est encore élément neutre dans ![]() .
.
![]() Si
Si ![]() ,
, ![]() est inversible d’inverse égal à
est inversible d’inverse égal à ![]() , donc
, donc ![]() .
.
On a prouvé que ![]() est un groupe .
est un groupe .
6.2. Sous-groupe
![]() Soit
Soit ![]() un groupe et
un groupe et ![]() une partie non vide de
une partie non vide de ![]() . Il y a équivalence entre
. Il y a équivalence entre
![]()
![]() est un sous-groupe de
est un sous-groupe de ![]() .
.
![]()
![]()
et ![]()
![]()
![]()
alors ![]() est un groupe.
est un groupe.
👍 : Pour démontrer que ![]() est non vide, on démontre que
est non vide, on démontre que ![]() contient l’élément neutre de
contient l’élément neutre de ![]() .
.
Remarque :
si ![]() est un sous groupe de
est un sous groupe de ![]() lui même sous-groupe de
lui même sous-groupe de ![]() ,
, ![]() est un sous-groupe de
est un sous-groupe de ![]() .
.
![]() exemples
exemples
![]()
![]() ,
, ![]() ,
, ![]() sont des sous-groupes pour la loi
sont des sous-groupes pour la loi ![]() de
de ![]() .
.
![]()
![]() ,
, ![]() sont des sous-groupes pour la loi
sont des sous-groupes pour la loi ![]() de
de ![]() .
.
![]()
![]() (ensemble des complexes de module 1) est un sous groupe de
(ensemble des complexes de module 1) est un sous groupe de ![]() et pour tout
et pour tout ![]() ,
, ![]() ,
, ![]() (ensemble des racines
(ensemble des racines ![]() -ièmes de 1) est un sous-groupe de
-ièmes de 1) est un sous-groupe de ![]() .
.
En cours d’année :
![]() L’ensemble
L’ensemble ![]() des automorphismes de
des automorphismes de ![]() est un sous-groupe de
est un sous-groupe de ![]() .
.
![]() Si
Si ![]() et
et ![]() , l’ensemble
, l’ensemble ![]() des matrices carrées d’ordre
des matrices carrées d’ordre ![]() à coefficients dans
à coefficients dans ![]() inversibles est un groupe pour la multiplication des matrices, appelé groupe spécial linéaire d’ordre
inversibles est un groupe pour la multiplication des matrices, appelé groupe spécial linéaire d’ordre ![]() .
.
6.3. Anneau
![]() Soit
Soit ![]() un ensemble non vide muni de deux lois de composition internes notées «
un ensemble non vide muni de deux lois de composition internes notées « ![]() » et «
» et « ![]() « .
« .
On dit que ![]() est un anneau si, et seulement si,
est un anneau si, et seulement si,
![]()
![]() est un groupe commutatif (l’élément neutre pour l’addition est noté
est un groupe commutatif (l’élément neutre pour l’addition est noté ![]() ou
ou ![]() s’il n’y a pas de confusion possible, le symétrique de
s’il n’y a pas de confusion possible, le symétrique de ![]() pour l’addition est noté
pour l’addition est noté ![]() )
)
![]() la multiplication est associative, possède un élément neutre noté
la multiplication est associative, possède un élément neutre noté ![]() (ou
(ou ![]() s’il n’y a pas de confusion possible) et la multiplication est distributive par rapport à l’addition.
s’il n’y a pas de confusion possible) et la multiplication est distributive par rapport à l’addition.
Si la multiplication est commutative, l’anneau est dit commutatif.
![]() Soient
Soient ![]() un anneau et
un anneau et ![]() une partie non vide.
une partie non vide.
Sur ![]() , on définit deux lois internes par
, on définit deux lois internes par
si ![]() ,
,
![]()
![]() est définie par
est définie par ![]()
![]()
![]() est définie par
est définie par ![]() .
.
![]() est un anneau commutatif.
est un anneau commutatif.
L’élément neutre pour l’addition est ![]() .
.
L’élément neutre pour la multiplication est ![]() .
.
⚠️ Si ![]() est un anneau,
est un anneau, ![]() et
et ![]() n’impliquent pas
n’impliquent pas ![]() .
.
h.p. Si ![]() est un anneau tel que si
est un anneau tel que si ![]() ou
ou ![]() , on dit que l’anneau est intègre.
, on dit que l’anneau est intègre.
En cours d’année, vous rencontrerez les anneaux suivants :
![]()
![]() l’anneau des polynômes à coefficients dans
l’anneau des polynômes à coefficients dans ![]()
![]()
![]() l’anneau des endomorphismes de
l’anneau des endomorphismes de ![]()
![]() Si
Si ![]() ,
, ![]() l’anneau des matrices carrées d’ordre
l’anneau des matrices carrées d’ordre ![]() à coefficients dans
à coefficients dans ![]() .
.
Calculs dans l’anneau ![]() ,
,
![]() Si
Si ![]() , on note
, on note ![]()
On note si ![]() et
et ![]()
![]()
![]() est défini par récurrence par
est défini par récurrence par
![]() ,
, ![]()
![]() et
et ![]()
Puis si ![]() .
.
![]()
![]() est défini par récurrence par
est défini par récurrence par
![]() et si
et si ![]()
Prop : Si ![]()
![]()
![]() ,
,
![]()
![]() et
et ![]()
![]() et
et ![]()
![]()
![]() ,
, ![]() .
.
![]() Soient
Soient ![]() un anneau et
un anneau et ![]() . Si
. Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() tels que ⚠️
tels que ⚠️ ![]() ,
,
![]() formule de Leibniz :
formule de Leibniz :
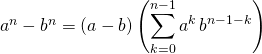
![]() binôme de Newton :
binôme de Newton :
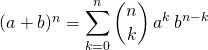 .
.
6.4. Corps
Un corps est un triplet ![]() tel que
tel que ![]() est un anneau commutatif contenant au moins deux éléments et tel que tout élément de
est un anneau commutatif contenant au moins deux éléments et tel que tout élément de ![]() est inversible pour la multiplication.
est inversible pour la multiplication.
exemples
![]() ,
, ![]() et
et ![]() sont des corps.
sont des corps.
En cours d’année, vous rencontrerez
![]() le corps des fractions rationnelles à coefficients dans
le corps des fractions rationnelles à coefficients dans ![]() .
.
Retrouvez gratuitement les chapitres à venir de Maths au programme de Maths Sup et les méthodes essentielles à la réussite de votre année en Maths Sup :

