Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Correction d’exercices sur les ensembles et applications en Math Sup
Résumé de cours Cours en ligne de Maths en Maths Sup
Plan des exercices : Bijection, Lois Internes, Anneaux
1. Sur les ensembles
2. Injection, surjection, bijection
3. Images directes et réciproques
4. Relations d’équivalence
5. Relations d’ordre
6. Lois internes
7. Groupes
8. Anneaux
9. Structure d’anneau sur ![]() .
.
COURS EN PREPA MATHS SUP
Les meilleurs professeurs particuliers en CPGE
POUR ACCÉLÉRER MA PROGRESSION EN PRÉPA
Avis Google France ★★★★★ 4,9 sur 5
1. Sur les ensembles
Exercice 1
Soient ![]() trois parties de
trois parties de ![]() .
.
![]() ssi
ssi ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() On suppose que
On suppose que ![]() .
.
Soit ![]() ,
, ![]() .
.
![]() et
et ![]() .
.
Comme ![]() ,
, ![]() .
.
On a prouvé l’inclusion
![]() .
.
En échangeant ![]() et
et ![]() , on obtient l’inclusion contraire, donc par double inclusion
, on obtient l’inclusion contraire, donc par double inclusion ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
L’implication précédente utilisée avec ![]() et
et ![]() donne
donne
![]() .
.
On a démontré l’équivalence.
Exercice 2
Soient ![]() trois parties de
trois parties de ![]() .
.
Trouver une condition nécessaire et suffisante pour que ![]() .
.
Correction : ![]() Analyse
Analyse
Si ![]() ,
,
![]()
![]() donc
donc ![]()
![]()
![]() donc
donc ![]()
On a prouvé que ![]() .
.
![]() Synthèse
Synthèse
Si ![]() ,
, ![]() et
et ![]() donc
donc ![]() .
.
On a démontré que ![]() .
.
Exercice 3
Soient ![]() ,
, ![]() et
et ![]() trois parties de
trois parties de ![]() . vérifiant
. vérifiant ![]() ,
, ![]() et
et ![]() .
.
Alors ![]() .
.
Vrai ou Faux ?
Correction : Soit ![]() .
.
![]() On suppose que
On suppose que ![]() , comme
, comme ![]() ,
, ![]() , donc
, donc ![]() alors
alors ![]() . On aboutit à une contradiction.
. On aboutit à une contradiction.
Il est impossible que ![]() .
.
![]() On a prouvé que
On a prouvé que ![]() . Comme
. Comme ![]() ,
, ![]() , donc
, donc ![]() .
.
Alors ![]() .
.
On a prouvé l’inclusion : ![]() .
.
Exercice 4
Soient ![]() ,
, ![]() et
et ![]() trois parties de
trois parties de ![]() .
.
Si ![]() et
et ![]() ,
, ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Soit ![]() .
.
On distingue deux cas :
![]()
![]() , alors
, alors ![]() , donc
, donc ![]() .
.
![]()
![]() ,
, ![]() avec
avec ![]() ,
, ![]() .
.
Dans les deux cas, ![]() .
.
On a prouvé que ![]() .
.
On a établi que ![]() .
.
2. Injection, surjection, bijection
Exercice 1
Soit ![]() une application de
une application de ![]() dans
dans ![]() telle que
telle que ![]() .
.
![]() est injective si, et seulement si,
est injective si, et seulement si, ![]() est surjective. Vrai ou Faux ?
est surjective. Vrai ou Faux ?
Correction :
![]() On suppose que
On suppose que ![]() est injective.
est injective.
Pour tout ![]() de
de ![]() ,
, ![]() , donc
, donc ![]() .
.
![]() étant injective,
étant injective, ![]() , donc il existe
, donc il existe ![]() dans
dans ![]() (
(![]() ) tel que
) tel que ![]() . On en déduit que
. On en déduit que ![]() est surjective.
est surjective.
On a donc prouvé que si ![]() est injective,
est injective, ![]() est surjective.
est surjective.
![]() On suppose que
On suppose que ![]() est surjective.
est surjective.
Soient ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() . Comme
. Comme ![]() est surjective, il existe
est surjective, il existe ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() et
et ![]() . L’hypothèse s’écrit
. L’hypothèse s’écrit ![]()
et en prenant l’image par ![]() :
: ![]() .
.
Comme ![]() , on en déduit que
, on en déduit que ![]() soit
soit ![]() .
.
On a ainsi prouvé que ![]() est injective.
est injective.
On a donc établi que si ![]() est surjective,
est surjective, ![]() est injective.
est injective.
On a donc prouvé que si ![]() est injective ou surjective,
est injective ou surjective, ![]() est bijective. En composant la relation
est bijective. En composant la relation ![]() par
par ![]() , on obtient
, on obtient ![]() .
.
Exercice 2
On note ![]() et
et
![]() ,
, ![]() .
.
Question 1
![]() est injective. Est-ce Vrai ou Faux ?
est injective. Est-ce Vrai ou Faux ?
Correction : Il est évident que ![]() est définie sur
est définie sur ![]() à valeurs dans
à valeurs dans ![]() .
.
On suppose que ![]() soit
soit ![]() donc
donc ![]() et
et ![]() .
.
On note ![]() .
.
![]() est tel que
est tel que ![]() et
et ![]() .
.
La relation ![]() donne
donne ![]() , puis
, puis ![]() (
(![]() ) et enfin
) et enfin ![]() car
car
![]() et
et ![]() . On en déduit que
. On en déduit que ![]() .
.
On a prouvé que ![]() , donc
, donc ![]() est injective.
est injective.
Exercice 2 (fin)
Question 2
![]() est-elle bijective ?
est-elle bijective ?
Correction : Soit ![]() , on cherche
, on cherche ![]() tel que
tel que ![]() .
.
On doit donc résoudre le système :
![]()
![]()
![]()
![]()
car ![]() .
.
Les valeurs ![]() et
et ![]() obtenues sont bien strictement positives.
obtenues sont bien strictement positives.
On a établi :
![]()
![]() .
.
On en déduit que ![]() est surjective.
est surjective.
En résumé, ![]() est une bijection de
est une bijection de ![]() sur
sur ![]() et
et ![]() .
.
Exercice 3
Soient ![]() une application de
une application de ![]() dans
dans ![]() ,
, ![]() une application de
une application de ![]() dans
dans ![]() et
et ![]() .
.
Question 1
Si ![]() est surjective et
est surjective et ![]() injective,
injective, ![]() est surjective. Vrai ou Faux ?
est surjective. Vrai ou Faux ?
Correction : Soit ![]() ,
, ![]() .
.
Comme ![]() est surjective, il existe
est surjective, il existe ![]() tel que
tel que ![]() soit
soit ![]() .
.
Comme ![]() est injective,
est injective, ![]() .
.
On a donc prouvé que ![]() est surjective.
est surjective.
Exercice 3 (fin)
Question 2
Si ![]() est injective et
est injective et ![]() surjective,
surjective, ![]() est injective. Vrai ou Faux ?
est injective. Vrai ou Faux ?
Correction : Soit ![]() tel que
tel que ![]() .
.
![]() est une surjection de
est une surjection de ![]() sur
sur ![]() .
.
Il existe ![]() et
et ![]() tels que
tels que ![]() et
et ![]()
donc ![]()
![]() .
.
![]() est injective, donc
est injective, donc ![]() alors
alors ![]() .
.
On a prouvé que ![]() est injective.
est injective.
Exercice 4
Soient ![]() et
et ![]() trois ensembles et
trois ensembles et ![]() une application de
une application de ![]() dans
dans ![]() .
.
Montrer que ![]() est injective ssi
est injective ssi ![]()
![]() .
.
Correction : ![]() On suppose que
On suppose que ![]() est injective.
est injective.
Soient ![]() et
et ![]() deux applications de
deux applications de ![]() dans
dans ![]() telles que
telles que ![]() .
.
Alors ![]() , donc
, donc ![]() , comme
, comme ![]() est injective, on en déduit que
est injective, on en déduit que ![]() .
.
![]() et
et ![]() sont deux applications de
sont deux applications de ![]() dans
dans ![]() telles que
telles que ![]() ,
, ![]() , alors
, alors ![]() .
.
![]() Au lieu de montrer que si
Au lieu de montrer que si ![]() , alors
, alors ![]() est injective, on démontre la contraposée.
est injective, on démontre la contraposée.
C’est à dire on démontre que si ![]() n’est pas injective, on peut trouver deux applications
n’est pas injective, on peut trouver deux applications ![]() et
et ![]() de
de ![]() dans
dans ![]() telles que
telles que ![]() et
et ![]() .
.
![]() n’est pas injective, donc il existe deux éléments distincts
n’est pas injective, donc il existe deux éléments distincts ![]() et
et ![]() de
de ![]() tels que
tels que ![]() ).
).
On définit ![]() et
et ![]() .
.
![]() et
et ![]() sont deux éléments distincts de
sont deux éléments distincts de ![]() .
.
Pour tout ![]() ,
, ![]()
![]() ,
,
ce qui prouve que ![]() .
.
On a donc établi que
si ![]()
![]() ,
,
alors ![]() est injective.
est injective.
STAGE INTENSIF MATHS SUP
Profite de tes vacances pour progresser en maths et physique
96% de réussite aux concours
84% dans le TOP 10
99% de recommandation à leurs amis
Avis Google France ★★★★★ 4,9 sur 5
3. images directes et réciproques
Exercice 1
Soit ![]() une application de
une application de ![]() dans
dans ![]() , montrer que
, montrer que ![]() est surjective si, et seulement si,
est surjective si, et seulement si, ![]() .
.
Correction : ![]() On suppose que
On suppose que ![]() est surjective. Soit
est surjective. Soit ![]() une partie quelconque de
une partie quelconque de ![]() .
.
![]() Pour tout
Pour tout ![]() , il existe
, il existe ![]() dans
dans ![]() tel que
tel que ![]() . Par définition de
. Par définition de ![]() ,
, ![]() , donc
, donc ![]() . On a donc établi que
. On a donc établi que ![]() .
.
![]() Soit
Soit ![]() . Comme
. Comme ![]() est surjective, il existe
est surjective, il existe ![]() tel que
tel que ![]() . Alors
. Alors ![]() donc
donc ![]() , on en déduit que
, on en déduit que ![]()
On a démontré que ![]() .
.
Donc si ![]() est surjective, pour toute partie
est surjective, pour toute partie ![]() de
de ![]() ,
, ![]() .
.
![]() On suppose que pour toute partie
On suppose que pour toute partie ![]() de
de ![]() ,
, ![]() .
.
En particulier pour ![]() ,
, ![]() .
.
Donc pour tout ![]() ,
, ![]() , il existe
, il existe ![]() donc
donc ![]() tel que
tel que ![]() .
.
On a établi que ![]() est surjective.
est surjective.
👍 On remarque que l’on a prouvé que
si ![]() , l’inclusion
, l’inclusion ![]() est vérifiée pour toute partie
est vérifiée pour toute partie ![]() de
de ![]() .
.
Exercice 2
Soit ![]() une application de
une application de ![]() dans
dans ![]() .
.
On note ![]() .
.
Question 1
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On remarque d’abord que pour tout ![]() ,
, ![]() :
:
car si ![]() , donc
, donc ![]() .
.
Alors ![]() et comme l’inclusion
et comme l’inclusion ![]() est évidente, par double inclusion,
est évidente, par double inclusion, ![]() , donc
, donc ![]() .
.
Exercice 2 (suite)
Question 2
Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() ,
, ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() , on suppose donc que
, on suppose donc que ![]() et
et ![]() .
.
Soit ![]() , alors
, alors ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() .
.
Comme ![]() ou
ou ![]() ,
, ![]() ou
ou ![]() , avec
, avec ![]() , donc
, donc ![]() ou
ou ![]() ), alors
), alors ![]() ou
ou ![]() .
.
D’après l’hypothèse sur ![]() et
et ![]() ,
, ![]() ou
ou ![]() soit
soit ![]() .
.
On a prouvé que ![]() .
.
Comme l’inclusion ![]()
est toujours vérifiée, par double inclusion, ![]() soit
soit ![]() .
.
Exercice 2 (suite)
Question 3
Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de ![]() ,
, ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() , on suppose donc que
, on suppose donc que ![]() et
et ![]() .
.
Soit ![]() , alors
, alors ![]() , donc il existe
, donc il existe ![]() tel que
tel que ![]() .
.
Puisque ![]() ,
, ![]() donc
donc ![]() , comme
, comme ![]() ,
, ![]() .
.
De même, ![]() donc
donc ![]() .
.
On a démontré que ![]() .
.
Comme on a toujours ![]() ,
,
par double inclusion,
![]() .
.
Exercice 2 (fin )
Question 4
![]() si, et seulement si,
si, et seulement si, ![]() est injective.
est injective.
4. Relations d’équivalence
Exercice 1
Soit ![]() un ensemble non vide et
un ensemble non vide et ![]() .
.
On rappelle que ![]() est l’ensemble des bijections de
est l’ensemble des bijections de ![]() sur
sur ![]() .
.
On définit sur ![]() la relation
la relation ![]() par
par
![]() .
.
![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() .
.
Vrai ou Faux ?
Correction : ![]() Soit
Soit ![]() et
et ![]() , alors
, alors ![]() donc
donc ![]() .
.
![]() est réflexive.
est réflexive.
![]() Soit
Soit ![]() vérifiant
vérifiant ![]() .
.
Il existe ![]() tel que
tel que ![]() alors
alors ![]() soit
soit ![]() avec
avec ![]() .
.
![]() est symétrique.
est symétrique.
![]() Soit
Soit ![]() vérifiant
vérifiant ![]() et
et ![]() .
.
Il existe ![]() tel que
tel que ![]() et
et ![]()
alors ![]()
par associativité de la loi ![]() ,
,
![]()
puis en utilisant ![]() en notant
en notant ![]() , on a montré que
, on a montré que ![]() donc
donc ![]() .
.
On a prouvé que ![]() est transitive.
est transitive.
![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() .
.
Exercice 2
Soit ![]() un ensemble contenant au moins deux éléments et
un ensemble contenant au moins deux éléments et ![]() un élément de
un élément de ![]() fixé.
fixé.
On définit ![]() sur
sur ![]() par :
par :
![]() ssi
ssi ![]() ou
ou ![]()
Question 1
![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() Soit
Soit ![]() .
.
![]() Si
Si ![]() ,
, ![]() donc
donc ![]() .
.
![]() Si
Si ![]() ,
, ![]() donc
donc ![]() , donc
, donc ![]() .
.
Par disjonction des cas, on a prouvé que ![]() .
.
La relation est réflexive.
![]() Soit
Soit ![]() ,
,
si ![]() , alors
, alors ![]() par commutativité de la loi
par commutativité de la loi ![]() .
.
La relation est symétrique.
![]() Soit
Soit ![]() ,
,
si ![]() et
et ![]() , on distingue les cas :
, on distingue les cas :
![]()
![]() et
et ![]() , alors
, alors ![]() donc
donc ![]() .
.
![]()
![]() et
et ![]() , alors
, alors ![]() donc
donc ![]() .
.
![]() Il est impossible d’avoir
Il est impossible d’avoir ![]() et
et ![]() , car on devrait avoir
, car on devrait avoir ![]() .
.
![]() Il est impossible d’avoir
Il est impossible d’avoir ![]() et
et ![]() , car on devrait avoir
, car on devrait avoir ![]() .
.
Par disjonction des cas, on a prouvé que ![]() .
.
![]() est transitive.
est transitive.
![]() est une relation d’équivalence sur
est une relation d’équivalence sur ![]() .
.
Exercice 2 (fin)
Question 2
Quel est le nombre de classes d’équivalence ?
Correction : ![]() Soit
Soit ![]() .
.
On remarque que ![]() ssi
ssi ![]()
car la relation ![]() est impossible et
est impossible et ![]() ssi
ssi ![]() .
.
Donc ![]() .
.
![]() Soit
Soit ![]() .
.
On remarque que ![]() ssi
ssi ![]()
car la condition ![]() est impossible et
est impossible et ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
Alors ![]() .
.
Toute partie ![]() de
de ![]() vérifie
vérifie
![]() soit
soit ![]() , alors
, alors ![]()
![]() soit
soit ![]() , alors
, alors ![]() .
.
On a donc trouvé toutes les classes d’équivalence.
Il y en a deux.
5. Relations d’ordre
Exercice 1
Soit ![]() un ensemble contenant au moins deux éléments et
un ensemble contenant au moins deux éléments et ![]() un élément de
un élément de ![]() fixé.
fixé.
Sur ![]() , on définit
, on définit ![]() par
par
![]() ssi
ssi ![]() ou
ou ![]() .
.
Question 1
![]() est une relation d’ordre sur
est une relation d’ordre sur ![]() .
.
Vrai ou Faux ?
Correction : ![]() Soit
Soit ![]() , comme
, comme ![]() ,
, ![]() .
.
La relation est réflexive.
![]() Soit
Soit ![]() ,
,
On suppose que ![]() et
et ![]() .
.
Si l’on avait ![]() , on aurait
, on aurait ![]() et
et ![]() , donc on aurait
, donc on aurait ![]() , ce qui est impossible.
, ce qui est impossible.
On a donc prouvé que ![]() .
.
La relation est antisymétrique.
![]() Soit
Soit ![]() ,
,
On suppose que ![]() et
et ![]() .
.
![]() Si
Si ![]() et
et ![]() alors
alors ![]() , donc
, donc ![]() .
.
![]() Si
Si ![]() et
et ![]() , alors
, alors ![]() donc
donc ![]() .
.
![]() Si
Si ![]() et
et ![]() , alors
, alors ![]() donc
donc ![]() .
.
![]() Les conditions
Les conditions ![]() et
et ![]() sont incompatibles car elles donnent
sont incompatibles car elles donnent ![]() et
et ![]() .
.
Par disjonction des cas, on a prouvé que ![]() .
.
La relation est transitive.
La relation ![]() est une relation d’ordre.
est une relation d’ordre.
Exercice 1 (suite)
Question 2
C’est une relation d’ordre total. Vrai ou Faux ?
Correction : On introduit ![]() tel que
tel que ![]() .
.
On note ![]() et
et ![]() .
.
![]()
![]() et
et ![]() , donc
, donc ![]() n’est pas vérifiée.
n’est pas vérifiée.
![]()
![]() et
et ![]() , donc
, donc ![]() n’est pas vérifiée.
n’est pas vérifiée.
Les éléments ![]() et
et ![]() ne sont pas comparables pour la relation
ne sont pas comparables pour la relation ![]() qui n’est pas totale.
qui n’est pas totale.
Exercice 2
Soit ![]() un ensemble et
un ensemble et ![]() une partie fixée de
une partie fixée de ![]() distincte de
distincte de ![]() et de
et de ![]() .
.
On définit la relation ![]() sur
sur ![]() par :
par :
![]() ,
, ![]() ssi
ssi ![]() et
et ![]() .
.
Question 1
![]() est une relation d’ordre sur
est une relation d’ordre sur ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() Pour tout
Pour tout ![]() et
et ![]() , donc
, donc ![]() .
.
La relation ![]() est une relation réflexive.
est une relation réflexive.
![]()
![]() , si
, si ![]() et
et ![]() .
.
![]() et
et ![]()
![]() et
et ![]()
![]() et
et ![]()
On termine en utilisant ![]()
![]() .
.
Donc la relation ![]() est antisymétrique.
est antisymétrique.
![]()
![]() ,
,
si ![]() et
et ![]() .
.
![]() et
et ![]() ,
,
![]() et
et ![]()
donc par transitivité de l’inclusion,![]() et
et ![]() .
.
On a prouvé que ![]() .
.
La relation est donc transitive.
La relation ![]() est une relation d’ordre sur
est une relation d’ordre sur ![]() .
.
Exercice 2 (suite)
Question 2
On a défini une relation d’ordre total ou partiel ?
Correction : Si l’on cherche à comparer ![]() et
et ![]() ,
,
![]() n’est pas inclus dans
n’est pas inclus dans ![]() donc
donc ![]() est fausse.
est fausse.
![]() n’est pas inclus dans
n’est pas inclus dans ![]() , donc
, donc ![]() est fausse.
est fausse.
On en déduit que ![]() et
et ![]() ne sont pas comparables pour la relation d’ordre
ne sont pas comparables pour la relation d’ordre ![]() . Il s’agit d’une relation d’ordre partiel.
. Il s’agit d’une relation d’ordre partiel.
Exercice 2 (fin)
Question 3.
![]() ,
, ![]() et
et ![]() .
.
![]() (resp.
(resp. ![]() ) est appelé plus grand élément (resp. plus petit élément) pour cette relation d’ordre.
) est appelé plus grand élément (resp. plus petit élément) pour cette relation d’ordre.
Vrai ou Faux ?
Correction : ![]() On démontre que
On démontre que ![]() est plus grand élément de
est plus grand élément de ![]() pour la relation
pour la relation ![]() :
:
![]() ,
, ![]() donc
donc ![]()
et ![]() ,
,
donc ![]() .
.
![]() On démontre que
On démontre que ![]() est le plus petit élément de P (E) pour la relation
est le plus petit élément de P (E) pour la relation ![]() :
:
![]() ,
, ![]() et
et ![]() , donc
, donc ![]() .
.
6. Loi de composition interne
Exercice 1
On suppose que ![]() est un ensemble non vide.
est un ensemble non vide.
Si ![]() , on note
, on note ![]() et si
et si ![]() .
.
On se donne ![]() et on note :
et on note : ![]() .
.
Question 1.
Si ![]() .
.
Vrai ou Faux ?
correction : On suppose que ![]()
Par associativité de la loi ![]() ,
,
![]()
comme ![]() ,
,
![]()
par associativité de la loi ![]() ,
,
![]()
comme ![]() ,
,
![]()
par associativité de la loi ![]() ,
,
![]()
donc ![]() .
.
⚠️ Justifiez les différentes étapes du raisonnement en déplaçant correctement les parenthèses.
Exercice 1 (suite)
Question 2
Pour tout ![]() .
.
Vrai ou Faux ?
Correction : Pour tout ![]() , soit
, soit ![]() .
.
![]()
![]() donc
donc ![]() et
et ![]() .
.
![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
![]()
Par ![]() ,
,
![]()
par associativité de la loi ![]() ,
,
![]()
par définition de ![]() ,
,
![]()
donc ![]() .
.
![]() est vraie.
est vraie.
La propriété est démontrée par récurrence.
Exercice 1 (suite)
Question 3
Si ![]() ,
, ![]() .
.
Vrai ou Faux ?
Correction : Soit ![]() . On note :
. On note :
![]() .
.
![]()
![]() est évidente car
est évidente car ![]() .
.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
![]()
par associativité,
![]()
comme ![]() ,
,
![]()
par associativité,
![]()
par ![]()
![]()
par associativité
![]()
et en utilisant la définition de ![]()
![]()
ce qui prouve ![]() .
.
La propriété est démontrée par récurrence.
Exercice 1 (fin)
Question 4
Si ![]() ,
, ![]() .
.
Vrai ou Faux ?
Correction : Soit ![]() . On note :
. On note :
![]()
![]() .
.
![]()
![]() est évidente car
est évidente car ![]() .
.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
![]() .
.
par ![]() ,
,
![]() .
.
Par associativité,
![]() .
.
en utilisant la question 3 par échange de ![]() et
et ![]()
![]() .
.
par associativité,
![]()
soit ![]()
ce qui prouve ![]() .
.
La propriété est démontrée par récurrence.
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

7. Groupes
Exercice 1
Soit ![]() un groupe. On suppose que
un groupe. On suppose que ![]() et
et ![]() sont deux sous-groupes de
sont deux sous-groupes de ![]() .
.
![]() est un sous-groupe de
est un sous-groupe de ![]() ssi
ssi ![]() ou
ou ![]() .
.
Vrai ou Faux ?
Correction : ![]() Si
Si ![]() ,
, ![]() est un sous-groupe de
est un sous-groupe de ![]() .
.
![]() Si
Si ![]() ,
, ![]() est un sous-groupe de
est un sous-groupe de ![]() .
.
![]() Si
Si ![]() n’est pas inclus dans
n’est pas inclus dans ![]() et
et ![]() n’est pas inclus dans
n’est pas inclus dans ![]() , il existe
, il existe ![]() tel que
tel que ![]() et
et ![]() tel que
tel que ![]() .
.
Soit ![]()
![]() Si
Si ![]() , alors
, alors ![]() serait un élément du groupe
serait un élément du groupe ![]() ce qui est exclu.
ce qui est exclu.
![]() Si
Si ![]() , alors
, alors ![]() serait un élément du groupe
serait un élément du groupe ![]() ce qui est exclu.
ce qui est exclu.
donc ![]() .
.
On a trouvé deux éléments ![]() et
et ![]() de
de ![]() tels que
tels que ![]() .
.
Donc ![]() n’est pas un sous-groupe de
n’est pas un sous-groupe de ![]() .
.
Exercice 2
On note si ![]()
![]() .
.
![]() est un groupe pour la loi
est un groupe pour la loi ![]() .
.
Vrai ou Faux ?
Correction : ![]()
![]() est une bijection de
est une bijection de ![]() dans lui même car
dans lui même car
si ![]() ,
, ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
donc l’équation ![]() admet une et une seule solution pour tout
admet une et une seule solution pour tout ![]() .
.
On remarque que l’on a prouvé en même temps que ![]()
Alors ![]() est une partie du groupe
est une partie du groupe ![]()
![]()
![]() est non vide car
est non vide car ![]() .
.
![]() Si
Si ![]() et
et ![]() .
.
![]()
![]()
![]()
![]() .
.
Comme ![]() ,
,
![]() .
.
![]() Et on avait prouvé que
Et on avait prouvé que ![]() .
.
Donc ![]() est un sous-groupe de
est un sous-groupe de ![]() .
.
Exercice 3
Soient ![]() un groupe et
un groupe et ![]() un sous-groupe de
un sous-groupe de ![]() .
.
Si ![]() , on note
, on note ![]() .
.
![]() est un sous-groupe de
est un sous-groupe de ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On note ![]() .
.
![]()
![]() est une partie de
est une partie de ![]() .
.
![]() Comme
Comme ![]() contient
contient ![]() ,
, ![]() contient
contient ![]() .
.
![]() Soit
Soit ![]() , il existe
, il existe ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() et
et ![]() .
.
![]()
![]()
![]()
![]() avec
avec ![]() , donc
, donc ![]() .
.
On a montré que ![]() est un sous-groupe de
est un sous-groupe de ![]() . C’est un groupe.
. C’est un groupe.
8. Anneau
Exercice 1
Soit ![]() est un anneau
est un anneau
On dit que ![]() est un diviseur de
est un diviseur de ![]() si
si ![]() et il existe
et il existe ![]() tel que
tel que ![]() ou
ou ![]() .
.
On note ![]() .
.
Question 1
Soit ![]() .
.
![]() ssi
ssi ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : ![]() On suppose que
On suppose que ![]() ,
,
![]() on peut donc introduire
on peut donc introduire
![]()
![]()
On simplifie :
![]()
![]()
donc
![]()
![]() On calcule
On calcule
![]()
![]()
On simplifie
![]()
![]()
donc ![]()
On a prouvé que
![]()
![]()
donc ![]() .
.
On a prouvé que
![]() si
si ![]() .
.
![]() En échangeant
En échangeant ![]() et
et ![]() , on obtient :
, on obtient :
![]() si
si ![]() .
.
Exercice 1 (fin)
Question 2
On suppose que ![]() ,
, ![]() et
et ![]() n’est pas un diviseur de
n’est pas un diviseur de ![]() .
.
Alors ![]() et
et ![]() sont éléments de
sont éléments de ![]() .
.
Vrai ou Faux ?
Correction : Comme ![]() , il existe
, il existe ![]() tel que
tel que ![]() .
.
On multiplie la relation ![]() à droite par
à droite par ![]() et à gauche par
et à gauche par ![]() , on obtient
, on obtient
![]() donc
donc ![]() .
.
Comme ![]() n’est pas un diviseur de
n’est pas un diviseur de ![]() ,
, ![]()
![]() On a donc prouvé que
On a donc prouvé que ![]() et par hypothèse
et par hypothèse ![]() donc
donc ![]() .
.
![]() On a prouvé que
On a prouvé que ![]() et par hypothèse
et par hypothèse ![]() donc
donc ![]() .
.
Exercice 2 : éléments nilpotents
Soit ![]() un anneau. On note
un anneau. On note ![]() l’élément neutre pour la multiplication.
l’élément neutre pour la multiplication.
On dit qu’un élément ![]() est nilpotent s’il existe
est nilpotent s’il existe ![]() tel que
tel que ![]() .
.
Question 1
Si ![]() est nilpotent, montrer que
est nilpotent, montrer que ![]() est inversible et calculer son inverse
est inversible et calculer son inverse
Correction : Si ![]() est nilpotent, on introduit
est nilpotent, on introduit ![]() tel que
tel que ![]() .
.
Les éléments ![]() et
et ![]() permutent, donc
permutent, donc
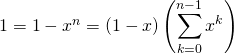
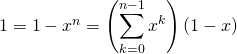
donc ![]() est inversible d’inverse égal
est inversible d’inverse égal ![]() .
.
Exercice 2 (suite)
Question 2
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() tels que
tels que ![]() soit inversible,
soit inversible, ![]() et
et ![]() soit nilpotent. Montrer que
soit nilpotent. Montrer que ![]() est inversible et donner son inverse.
est inversible et donner son inverse.
Correction : ![]() On démontre par récurrence que pour tout
On démontre par récurrence que pour tout ![]() ,
, ![]() .
.
![]() est vraie par hypothèse sur
est vraie par hypothèse sur ![]() et
et ![]() .
.
Si ![]() est vraie, alors
est vraie, alors ![]()
par associativité, puis par ![]() ,
,
![]()
puis en utilisant ![]() et l’associativité,
et l’associativité,
![]() .
.
La propriété est démontrée par récurrence.
![]() On démontre par récurrence que pour tout
On démontre par récurrence que pour tout ![]() ,
, ![]() .
.
![]() est évidente.
est évidente.
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
en utilisant la première partie.
![]() .
.
La propriété est démontrée par récurrence.
![]() On note
On note ![]() .
.
Si ![]() ,
, ![]()
soit ![]() .
.
![]() On introduit
On introduit ![]() tel que
tel que ![]() .
.
On a montré que ![]() et la deuxième partie ci-dessus donne :
et la deuxième partie ci-dessus donne :
![]()
et ![]() .
.
Par la question1, ![]() est inversible, soit
est inversible, soit ![]() est inversible. Puis comme
est inversible. Puis comme ![]() est inversible, par produit
est inversible, par produit ![]() est inversible.
est inversible.
👍 On a démontré des propriétés utiles dans d’autres exercices.
Dans un anneau ![]() , si
, si ![]() ,
,
![]()
![]() et
et ![]() .
.
On pourrait en déduire que ![]() .
.
Si de plus ![]() est inversible,
est inversible, ![]() .
.
Exercice 2 (suite)
Question 3
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]() tels que
tels que ![]() .
.
a) Si ![]() et
et ![]() sont nilpotents et
sont nilpotents et ![]() , montrer que
, montrer que ![]() est nilpotent.
est nilpotent.
b) Si ![]() est nilpotent et si
est nilpotent et si ![]() , montrer que
, montrer que ![]() est nilpotent.
est nilpotent.
c) Si ![]() est nilpotent, montrer que
est nilpotent, montrer que ![]() est nilpotent.
est nilpotent.
Correction : ![]() Partie a)
Partie a)
On note ![]() tels que
tels que ![]() et
et ![]() .
.
![]() Si
Si ![]() , on peut utiliser la formule du binôme de Newton,
, on peut utiliser la formule du binôme de Newton,
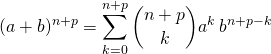
![]() si
si ![]() ,
, ![]() donc
donc ![]() et
et ![]() .
.
![]() si
si ![]() ,
, ![]() , donc
, donc ![]() .
.
Par somme, ![]() ,
, ![]() est nilpotent.
est nilpotent.
![]() Partie b)
Partie b)
On a vu aussi dans la question 2 que ![]() si
si ![]() .
.
Comme ![]() ,
, ![]() .
.
![]() est nilpotent.
est nilpotent.
![]() Partie c)
Partie c)
On établit par récurrence :
Si ![]() ,
, ![]() .
.
![]()
![]() .
.
On a démontré que ![]() est vraie.
est vraie.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
![]()
![]() .
.
Ce qui prouve ![]() .
.
![]() On suppose que
On suppose que ![]() est nilpotent. Il existe donc
est nilpotent. Il existe donc ![]() tel que
tel que ![]() .
.
![]() .
.
On a prouvé que ![]() est nilpotent.
est nilpotent.
9. Structure d’anneau sur  .
.
Exercice
On définit si ![]() ,
,
![]() .
.
Question 1
Montrer que ![]() .
.
Exprimer la fonction indicatrice de ![]() à l’aide des fonctions indicatrices de
à l’aide des fonctions indicatrices de ![]() et de
et de ![]() .
.
Question 3
La loi ![]() est-elle commutative ?
est-elle commutative ?
Question 4
Montrer que la loi ![]() est associative.
est associative.
Question 5
![]() est-il un groupe commutatif ?
est-il un groupe commutatif ?
Pour accéder aux meilleurs cours particuliers à domicile ou en ligne, sélectionner le prof qu'il vous faut

Tous le programme de Maths en Maths Sup est disponible en cours en ligne, retrouvez par exemple les chapitres suivants :

