Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Cours : Équations différentielles en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Résumé de cours et méthodes – Equations différentielles en Maths Sup
Plan :
1. Équation différentielle linéaire du premier ordre
![]() 1.1. Équation homogène
1.1. Équation homogène
![]() 1.2. Ensemble des solutions
1.2. Ensemble des solutions
![]() 1.3. Recherche d’une solution particulière de
1.3. Recherche d’une solution particulière de ![]()
![]() 1.4. Théorème de Cauchy-Lipschitz
1.4. Théorème de Cauchy-Lipschitz
![]() 1.5. Consignes de rédaction
1.5. Consignes de rédaction
![]() 1.6. Raccordement de solutions (en cours d’année).
1.6. Raccordement de solutions (en cours d’année).
2. Équation différentielle linéaire du second ordre à coefficients constants.
![]() 2.1. Équation homogène
2.1. Équation homogène
![]() 2.2. Ensemble des solutions
2.2. Ensemble des solutions
![]() 2.3. Recherche d’une solution particulière de
2.3. Recherche d’une solution particulière de ![]()
![]() 2.4. Théorème de Cauchy-Lipschitz
2.4. Théorème de Cauchy-Lipschitz
![]() 2.5. Consignes de rédaction.
2.5. Consignes de rédaction.
1. Équation différentielle linéaire du premier ordre
On note ![]()
![]() où
où ![]() sont des fonctions continues sur un intervalle
sont des fonctions continues sur un intervalle ![]() à valeurs dans
à valeurs dans ![]() .
.
1.1. Résolution de l’équation sans second membre ![]() .
.
On détermine une primitive ![]() de
de ![]() sur l’intervalle
sur l’intervalle ![]() .
.
La solution générale de ![]() est donnée par :
est donnée par : ![]() où
où ![]() .
.
Cas particulier :
si ![]() , l’ensemble des solutions de
, l’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() ,
, ![]() où
où ![]() .
.
👍 Dans le cas où ![]() , une solution de
, une solution de ![]() est soit nulle sur
est soit nulle sur ![]() , soit ne s’annule pas sur
, soit ne s’annule pas sur ![]() et garde alors un signe constant sur
et garde alors un signe constant sur ![]() .
.
Donc lorsque la solution générale de ![]() s’écrit sous la forme
s’écrit sous la forme ![]() où
où ![]() ,
,
comme la fonction ![]() ne s’annule pas sur
ne s’annule pas sur ![]() , elle a un signe constant donc la solution générale de
, elle a un signe constant donc la solution générale de ![]() peut s’écrire
peut s’écrire
![]() ou
ou ![]() donc en résumé sous la forme
donc en résumé sous la forme ![]() où
où ![]() .
.
On peut donc « supprimer » la valeur absolue.
exemple :
solution générale de ![]()
![]()
Correction : La solution générale sur ![]() ou sur
ou sur ![]() est
est ![]() (car
(car ![]() soit encore
soit encore ![]() où
où ![]() .
.
👍 Un peu plus tard dans l’année, vous pourrez dire que l’ensemble ![]() des solutions de
des solutions de ![]() sur
sur ![]() est un espace vectoriel de dimension 1 de base
est un espace vectoriel de dimension 1 de base ![]() .
.
1.2. Ensemble des solutions
![]() On note
On note ![]()
![]() et
et ![]()
La solution générale de ![]() est la somme de la solution générale de
est la somme de la solution générale de ![]() et d’une solution particulière de
et d’une solution particulière de ![]() .
.
![]() Principe de superposition des solutions.
Principe de superposition des solutions.
On suppose que ![]() où
où ![]() et
et ![]() et
et ![]() sont continues sur
sont continues sur ![]() .
.
Si ![]() (resp
(resp ![]() ) est solution particulière de
) est solution particulière de ![]()
(resp. de ![]() )
)
![]() est solution particulière de
est solution particulière de ![]() .
.
1.3. Détermination d’une solution particulière de ![]() .
.
![]() Elle peut être évidente.
Elle peut être évidente.
![]() Sinon, on utilise la méthode de variation de la constante.
Sinon, on utilise la méthode de variation de la constante.
Ayant trouvé comme solution de ![]() ,
, ![]() , on note
, on note ![]() .
.
On écrit que ![]() est solution de
est solution de ![]() sur
sur ![]() Le terme en
Le terme en ![]() doit disparaître et on obtient :
doit disparaître et on obtient :
![]() est solution sur
est solution sur ![]() de
de ![]()
ssi ![]()
ssi ![]() .
.
👍
![]() En général, on peut déterminer une primitive de
En général, on peut déterminer une primitive de ![]() .
.
![]() Si l’on ne sait pas déterminer une primitive de cette fonction à l’aide des fonctions usuelles, on introduit
Si l’on ne sait pas déterminer une primitive de cette fonction à l’aide des fonctions usuelles, on introduit ![]() et on dit que
et on dit que ![]()
![]() .
.
Dans ce cas, l’ensemble des solutions sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() ,
, ![]()
où ![]() .
.
![]() On termine en donnant l’ensemble des solutions, ou en cherchant la solution vérifiant la condition initiale donnée par l’énoncé.
On termine en donnant l’ensemble des solutions, ou en cherchant la solution vérifiant la condition initiale donnée par l’énoncé.
en MPSI 👍 Un peu plus tard dans l’année, vous pourrez dire que l’ensemble ![]() des solutions de
des solutions de ![]() sur
sur ![]() est un sous-espace affine de l’espace vectoriel des fonctions dérivables sur
est un sous-espace affine de l’espace vectoriel des fonctions dérivables sur ![]() à valeurs dans
à valeurs dans ![]() .
.
1.4. Théorème de Cauchy-Lipschitz
Théorème de Cauchy-Lipschitz :
Si les fonctions ![]() et
et ![]() sont continues sur l’intervalle
sont continues sur l’intervalle ![]() ,
,
pour tout ![]() , il existe une unique solution
, il existe une unique solution ![]() de
de
![]()
vérifiant ![]() .
.
Remarque : Elle peut s’exprimer sous la forme : si ![]() ,
, ![]() avec
avec ![]() .
.
1.5. Consignes de rédaction
Soit ![]() .
.
Dans la suite, ![]() est un intervalle sur lequel les fonctions
est un intervalle sur lequel les fonctions ![]() et
et ![]() sont continues.
sont continues.
On note ![]() si les fonctions
si les fonctions ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() et
et ![]() si les fonctions
si les fonctions ![]() et
et ![]() sont à valeurs dans
sont à valeurs dans ![]() .
.
![]() Noter
Noter ![]() .
.
Dire : on introduit ![]() une primitive de
une primitive de ![]() sur l’intervalle
sur l’intervalle ![]() ,
,
la solution générale de ![]() sur
sur ![]() est la fonction
est la fonction ![]() où
où ![]() .
.
Lorsque ![]() , terminer la rédaction par :
, terminer la rédaction par :
l’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() où
où ![]() .
.
![]() Lorsqu’il y a un second membre et pas de solution particulière évidente, dire :
Lorsqu’il y a un second membre et pas de solution particulière évidente, dire :
on cherche une solution particulière par la méthode de variation de la constante. On écrit :
![]() est solution de
est solution de ![]() sur
sur ![]()
ssi ![]()
ssi ![]()
ssi ![]() où
où ![]() est une primitive sur
est une primitive sur ![]() de
de ![]() .
.
![]() Terminer en disant au choix :
Terminer en disant au choix :
![]() la solution générale de
la solution générale de ![]() sur
sur ![]() est définie par
est définie par ![]() ,
, ![]() où
où ![]() .
.
ou
![]() l’ensemble des solutions de
l’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() ,
, ![]() où
où ![]()
ou encore
![]()
![]() (ensemble des solutions de
(ensemble des solutions de ![]() sur
sur ![]() ) est égal à l’ensemble
) est égal à l’ensemble
![]() .
.
1.6. Raccordement de solutions
⚠️ Paragraphe utile en cours d’année, les raisonnements nécessitent en général des équivalents et des développements limités.
Résolution de
![]() .
.
Supposons pour fixer les idées que ![]() et que
et que ![]() ne s’annule qu’en un point
ne s’annule qu’en un point ![]() de
de ![]() .
.
On note ![]() et
et ![]() , en divisant par
, en divisant par ![]() on obtient une équation dite normalisée de la forme
on obtient une équation dite normalisée de la forme
![]() :
: ![]() où les fonctions
où les fonctions ![]() et
et ![]() sont continues sur chacun des intervalles
sont continues sur chacun des intervalles ![]() et
et ![]() .
.
![]() On résout
On résout ![]() sur chacun des intervalles
sur chacun des intervalles ![]() et
et ![]() .
.
👍 : il est en général possible de poser ![]() et de résoudre
et de résoudre ![]() sur
sur ![]() sans être obligé de le faire deux fois.
sans être obligé de le faire deux fois.
Il faudra à la fin donner l’ensemble des solutions sur ![]() puis l’ensemble des solutions sur
puis l’ensemble des solutions sur ![]() . Il est conseillé de nommer les constantes définissant la solution générale par des lettres différentes.
. Il est conseillé de nommer les constantes définissant la solution générale par des lettres différentes.
![]() On pose
On pose
![]()
où ![]() est solution de
est solution de ![]() sur
sur ![]() et
et ![]() est solution de
est solution de ![]() sur
sur ![]() .
.
![]() Puis
Puis
![]() a) on cherche s’il est possible (en choisissant éventuellement les constantes) de prolonger
a) on cherche s’il est possible (en choisissant éventuellement les constantes) de prolonger ![]() par continuité en
par continuité en ![]() , donc en démontrant que la limite à gauche de
, donc en démontrant que la limite à gauche de ![]() de la fonction
de la fonction ![]() est égale à la limite à droite de
est égale à la limite à droite de ![]() en
en ![]() .
.
Si c’est le cas,
![]() b) on cherche si la fonction
b) on cherche si la fonction ![]() est dérivable en
est dérivable en ![]() .
.
Si c’est le cas,
![]() c) on cherche si
c) on cherche si ![]() est encore solution de
est encore solution de ![]() en
en ![]() .
.
Dans ce cas, la (ou les) fonction(s) obtenue(s) est (sont) solution(s) de ![]() sur
sur ![]() .
.
On dit que l’on a raccordé les solutions en ![]() .
.
COURS DE MATHS
Nous avons recruté pour vous les meilleurs professeurs particuliers de maths
S'EXERCER ET APPRENDRE
Avis Google France ★★★★★ 4,8 sur 5
2. Équation différentielle linéaire du second ordre à coefficients constants.
Hypothèses : soit à résoudre l’équation ![]()
où ![]() et
et ![]() est une fonction continue sur
est une fonction continue sur ![]() à valeurs dans
à valeurs dans ![]() . On note
. On note ![]() .
.
2.1. Résolution de ![]() où
où ![]() .
.
On note ![]() .
.
Si l’équation caractéristique ![]()
![]() a deux racines distinctes
a deux racines distinctes ![]() et
et ![]() dans
dans ![]() , on introduit :
, on introduit :
… ![]()
… ![]() .
.
![]() a une racine double
a une racine double ![]() , on introduit :
, on introduit :
… ![]()
… ![]() .
.
![]()
![]() , complexes conjuguées :
, complexes conjuguées : ![]() et
et ![]() , où
, où ![]() , on introduit :
, on introduit :
… ![]()
… ![]() .
.
Dans chacun des trois cas, l’ensemble des solutions de ![]() s’écrit
s’écrit
![]() .
.
![]() et pour aller plus vite : dans le cas
et pour aller plus vite : dans le cas ![]() avec
avec ![]()
… ![]()
… ![]() .
.
![]() et pour aller plus vite : dans le cas
et pour aller plus vite : dans le cas ![]() avec
avec ![]()
… ![]()
… ![]() .
.
ou
… ![]()
… ![]() .
.
👍 Un peu plus tard dans l’année, vous pourrez dire que l’ensemble ![]() des solutions de
des solutions de ![]() sur
sur ![]() est un espace vectoriel de dimension 2 de base
est un espace vectoriel de dimension 2 de base ![]() .
.
2.2. Ensemble des solutions
![]() On note
On note ![]() et
et ![]()
La solution générale de ![]() est la somme de la solution générale de
est la somme de la solution générale de ![]() et d’une solution particulière de
et d’une solution particulière de ![]() .
.
![]() Principe de superposition des solutions.
Principe de superposition des solutions.
On suppose que ![]() où
où ![]() et
et ![]() et
et ![]() sont continues sur
sont continues sur ![]() .
.
Si ![]() (resp
(resp ![]() ) est solution particulière de
) est solution particulière de ![]()
(resp. de ![]() )
)
![]() est solution particulière de
est solution particulière de ![]() .
.
2.3. Recherche d’une solution particulière de ![]()
![]() où
où ![]()
On note ![]() .
.
![]() M1. Penser au principe de superposition des solutions pour trouver une solution particulière avec un second membre plus simple.
M1. Penser au principe de superposition des solutions pour trouver une solution particulière avec un second membre plus simple.
![]() M2. Utilisation de la fonction conjuguée.
M2. Utilisation de la fonction conjuguée.
Si ![]() et si
et si ![]() ,
, ![]() est solution de
est solution de ![]() la fonction
la fonction ![]() ,
, ![]() est solution de
est solution de ![]() .
.
![]() M3. Cas où
M3. Cas où ![]() où
où ![]()
![]() Si
Si ![]() , on cherche une solution particulière sous la forme
, on cherche une solution particulière sous la forme
![]() où
où ![]() .
.
![]() Si
Si ![]() et
et ![]() , on cherche une solution particulière sous la forme
, on cherche une solution particulière sous la forme
![]() où
où ![]() .
.
![]() Si
Si ![]() , on cherche une solution particulière sous la forme
, on cherche une solution particulière sous la forme
![]() où
où ![]() .
.
![]() M4.
M4. ![]() ou
ou ![]()
![]() Chercher une solution particulière
Chercher une solution particulière ![]() à valeurs complexes de
à valeurs complexes de
![]() .
.
![]()
![]() est une solution particuliè- re de
est une solution particuliè- re de ![]()
![]()
![]() est une solution particuliè- re de
est une solution particuliè- re de ![]() .
.
![]() M5. Second membre de la forme
M5. Second membre de la forme ![]() fonction polynôme de degré
fonction polynôme de degré ![]() à coefficients dans
à coefficients dans ![]() de degré
de degré ![]() et avec
et avec ![]() , chercher une solution sous la forme d’une fonction polynôme de même degré.
, chercher une solution sous la forme d’une fonction polynôme de même degré.
Justification de M5 : On suppose que 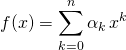 .
.
On cherche 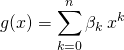
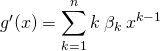
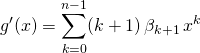
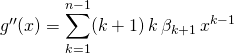
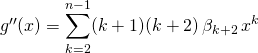
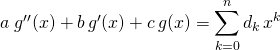
où ![]() ,
, ![]()
et si ![]() ,
, ![]()
![]() .
.
Le système ![]() admet une unique solution lorsque
admet une unique solution lorsque ![]() (on commence par résoudre le cas
(on commence par résoudre le cas ![]() puis
puis ![]() etc … pour terminer par
etc … pour terminer par ![]() ).
).
PROF DE MATHS PARTICULIER
Des cours de qualité et enseignants aguerris
Préparer des concours ou s'exercer
Avis Google France ★★★★★ 4,9 sur 5
2.4. Théorème de Cauchy-Lipschitz
Soit ![]()
Soit ![]() une fonction continue sur l’intervalle
une fonction continue sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() .
.
Pour tout ![]() et
et ![]() ,
,
il existe une unique solution ![]() de
de ![]()
vérifiant ![]() et
et ![]() .
.
2.5. Consignes de rédaction
![]() Résoudre d’abord l’équation homogène
Résoudre d’abord l’équation homogène ![]() , introduire les fonctions
, introduire les fonctions ![]() et
et ![]() définies dans le paragraphe 2.3. selon la valeur de
définies dans le paragraphe 2.3. selon la valeur de ![]() .
.
Et écrire que l’ensemble des solutions de ![]() est
est
![]()
![]() Dans le cas où il y a un second membre, déterminer une solution particulière
Dans le cas où il y a un second membre, déterminer une solution particulière ![]() de
de ![]() et écrire
et écrire
![]()
![]() est égal à
est égal à ![]()
![]() ou
ou ![]() où
où ![]() est solution générale de
est solution générale de ![]() .
.
![]() S’il y a lieu déterminer la ou les solution(s) vérifiant la ou les condition(s) initiales(s) donnée(s).
S’il y a lieu déterminer la ou les solution(s) vérifiant la ou les condition(s) initiales(s) donnée(s).
Les mathématiques représentent la matière la plus importante pour les étudiants de Maths Sup. Révisez ses cours de maths régulièrement est donc fondamental pour réussir. Pour cela découvrez de nombreux autres cours en ligne et nos profs de maths particulier pour les MPSI, PTSI, MP2I et PCSI :

