Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Les espaces euclidiens en Maths Sup MPSI, MP2I, PCSI, PTSI

Ce cours en ligne de Maths Sup sur les espaces euclidiens vient compléter le cours sur les espaces vectoriels et le cours sur les espaces préhilbertiens. Des cours qui sont essentiels en Maths Sup, mais également, fondamentaux pour aborder sereinement les maths au programme de Maths Spé que vous pouvez aborder avec un prof de maths à domicile.

A. Espace vectoriel euclidien $E$ en Maths Sup

1. Base orthonormale d’un espace euclidien $E$

$\bullet$ M1 : Si $E$ est un espace euclidien de dimension $n > 0$ , $E$ admet une base orthonormale.

$\bullet$ M2 : Toute famille orthonormale d’un espace euclidien $E$ peut être complétée en une base orthonormale de $E$ .

$\bullet$ M3 : Si $\mathcal{B} = (e_i)_{1 \leqslant i \leqslant n}\,$ est une base orthonormale de $E$ ,

$\ast$ $\forall \, x \in E,\; \displaystyle x = \sum_ {i = 1} ^n (x \, | \, e_i) \, e_i \,$ .

$\ast$ $\forall \, (x , \,y) \in E^2$ ,

si $\displaystyle x = \sum_{i = 1} ^n x_i \, e_i\,$ et $\displaystyle y = \sum_{i = 1} ^n y_i \, e_i\,$ , $\qquad \qquad \displaystyle (x\, | \, y) = \sum_{i = 1} ^n x_i \, y_i\,$ .

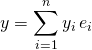$\ast$ Si l’on note $X$ et $Y$ les matrices colonnes de $x$ et $y$ dans la base $\mathcal{B}$ , $(x \, | \, y ) = X^{\textrm{T} } \; Y$ .

$\ast$ Si $x = \displaystyle \sum _{k = 1} ^n \, x_k \, e_k\,$ , $\displaystyle \Vert x \Vert = \sqrt {\sum _ {k = 1} ^n x_k ^2} \,$ .

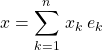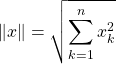$\bullet$ M4 : Théorème de la base orthonormale incomplète.
Si $E$ est un espace euclidien de dimension $n$ et si $(e_1\,\, \cdots \, ,\, e_p)$ est une famille orthonormale de $E$ , il existe une base orthonormale de $E$ de la forme $(e_1\,,\, \cdots \, ,\, e_p\, ,\, e_{p + 1} \,,\, \,\cdots \, ,\, e_n)$ .

2. Supplémentaire orthogonal en Maths Sup

$E$ est un espace euclidien.

$\bullet$ M1 : Si $F$ est un sous-espace de $E$ ,

$\ast$ $E = F \oplus F ^{\perp}$

$\ast$ $\dim F ^{\perp} = \dim E - \dim F$ .

$\bullet$ M2 : Si $F$ est un sous espace vectoriel de $E$ , $\left ( F ^{\perp} \right ) ^{\perp} = F$ .

$\bullet$ M3 : On suppose que $E = F \oplus G$ .

Si $\forall\, f \in F$ , $\forall \, g \in G$ , $(f \mid g) = 0$ ,

$\ast$ $G = F ^{\perp}$

$\ast$ $F = G ^{\perp}$ .

$\bullet$ M4 : Si $E$ est un espace euclidien de dimension $n$ , de base orthonormale

$\mathcal{B} = (e_1\, ,\, \cdots \, , e_n)$ , si $p \in [\![1,\, n - 1]\!]$

et $F = \textrm{Vect} (e_1\, ,\, \cdots \, , e_p)$

$\qquad F^{\perp} = \textrm{Vect} (e_{p+1}\, ,\, \cdots \, , e_n)$ .

$\bullet$ M5 : Si $F$ est un s.e.v. de $E$ , la projection orthogonale $p_F$ sur $F$ vérifie

$\ast$ pour tout $x \in E$ , $x - p_F(x) \perp p_F(x)$

$\ast$ $p_F(x)$ est le seul vecteur de $F$ qui rend minimum $\Vert x - f\Vert$ lorsque $f \in F$

$\ast$ la distance de $x \in E$ à $F$ est égale à $\textrm{d} (x , \, F) = \Vert x - p_F(x) \Vert$

et $\textrm{d}^2(x , \, F) = \Vert x \Vert ^2 - \Vert p_F(x)\Vert ^2$ .

$\bullet$ M6 : Si $F$ est un s.e.v. de $E$ de base orthonormale directe $(u_1\, ,\, \cdots \, , \, u_k)$

$\quad \forall\, x \in E, \, p_F(x) = \displaystyle \sum _{i = 1} ^k (x \mid u_i) \, u _ i\,$ .

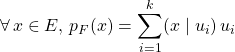COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

B. Hyperplans et hyperplans affines en Maths Sup

1. Hyperplans en Maths Sup

Soit $H$ un hyperplan de $\mathbb{R}^n$ d’équation 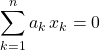$\displaystyle \sum _ {k = 1} ^n a_k \, x_k = 0$ dans la base canonique.

$\bullet$ M1 : $H^{\perp}$ est la droite dirigée par $a = (a_1\, ,\, \cdots \, , \, a_n)$ .

Le vecteur $a$ est appelé vecteur normal à l’hyperplan.

$H = \left ( \textrm{Vect}(a) \right ) ^{\perp}$ .

$\bullet$ M2 : La projection orthogonale sur $\textrm{Vect}(a)$ est $E \to E,\, x \mapsto \displaystyle \frac {(a \mid x) } {\Vert a \Vert ^2} \, a$ .

$\bullet$ M3 : La projection orthogonale sur $H$ est $p_H : E \to E,\, x \mapsto \displaystyle x - \frac {(a \mid x) } {\Vert a \Vert ^2} \, a$ .

$\bullet$ M4 : La distance de $x$ à $H$ est égale à $\displaystyle \frac {\vert (a \mid x) \vert} {\Vert a \Vert }$ .

$\bullet$ M5 : Le carré de la distance de $x$ à $\textrm{Vect}(a)$ est égal à $\displaystyle \Vert x \Vert ^2 - \frac {(a \mid x) ^2 } {\Vert a \Vert ^2}$ .

2. Hyperplans affines en Maths Sup

On suppose l’espace rapporté à un repère orthonormal $\mathcal{R}$ .

$\bullet$ D : un hyperplan affine passant par $A$ de direction $H$ est le sous espace affine passant par $A$ et de direction l’hyperplan $H$ de $E$ soit l’ensemble

$\qquad \qquad \{M \, / \, \overrightarrow {AM} \in H\}$ .

$\bullet$ M : $\mathcal{H}$ est un hyperplan affine de $\mathbb{R}^n$ ssi il existe $d\in \mathbb{R}$ et $(a_1\, ,\, \cdots \, ,\, a_n) \neq 0$ tels que $\mathcal{H}$ soit l’ensemble des points $M$ de coordonnées $(x_1\, ,\, \cdots \, , \, x_n)$ vérifiant

$\displaystyle \sum _ {i = 1} ^n a_i \, x _ i = d$ .

La direction de $\mathcal{H}$ est l’hyperplan d’équation $\displaystyle \sum _ {i = 1} ^n a_i \, x_i = 0$ .

On dit que le vecteur de coordonnées $(a_1\, ,\, \cdots \, ,\, a_n)$ est un vecteur normal à l’hyperplan $\mathcal{H}$ .

$\bullet$ P : La distance de $M$ à l’hyperplan affine passant par $A$ et de vecteur normal $\overrightarrow {n}$ est égale à $\left \vert (\overrightarrow {AM} \mid \overrightarrow{n}) \right \vert$ .

C. Caractérisation des isométries et des matrices orthogonales

1. Isométries en Maths Sup

$\bullet$ Si $E$ est un espace vectoriel euclidien de dimension $n$ et si $u \in \mathcal{L} (E)$ , il y a équivalence entre :

1. $u$ est une isométrie (ou un automorphisme orthogonal),

2. $\forall \, (x ,\, y) \in E^2,$

$\quad \quad \quad \; (u(x)\, | \, u(y)) = (x \, |\, y)$ ,

3. $\forall \, x \in E,\; \Vert u(x)\Vert =\Vert x\Vert$ ,

4. pour toute base orthonormale $\mathcal{B}$ de $E,$ $u(\mathcal{B})$ est une base orthonormale de $E$ ,

5. il existe une base orthonormale $\mathcal{B}$ de $E$ telle que $u(\mathcal{B})$ soit une base orthonormale de $E$ ,

6. la matrice de $u$ dans une base orthonormale est une matrice orthogonale.

$\ast$ On note $O(E)$ l’ensemble des isométries de $E$ , $O(E)$ est un sous-groupe de $(\textrm{GL}_n(\mathbb{R}), \, \circ)$ appelé groupe orthogonal de $E$ .

$\ast$ Si $u$ est une isométrie, $\det(u) = \pm 1$ .

$\ast$ On note $SO(E)$ l’ensemble des rotations de $E$ (isométries de $E$ de déterminant égal à 1), $SO(E)$ est un sous-groupe de $O(E)$ appelé groupe spécial orthogonal de $E$ .

2. Matrices orthogonales en Maths Sup

$\bullet$ Soit $M \in \mathcal{M}_n (\mathbb {R})$ .

On note $(C_1\, ,\, C_2 \,, \, \cdots \, , \, C_n)$ le système de ses vecteurs colonnes.

Il y a équivalence entre :

1. $M$ est une matrice orthogonale,

2. $M^{\textrm{T}}\, M = \textrm{I}_n\,$ ,

3. $M\, M^{\textrm{T}} = \textrm{I}_n \,$ ,

4. $M^{- 1} = M^{\textrm{T}}$ ,

5. $(C_1\, ,\, C_2 \,, \, \cdots \, , \, C_n)$ est une base orthonormale de l’espace vectoriel euclidien $\mathbb{R} ^n$ pour la structure euclidienne canonique,

6. $\forall\, (i , \, j) \in [\![1 , \, n]\!]^2 , \; (C_i \, | \, C_j ) = \delta_{i , \, j} \;$ ,

7. $M$ est la matrice d’une isométrie de $E$ , espace euclidien de dimension $n$ , dans une base orthonormale.

$\ast$ On note $O_n(\mathbb{R})$ l’ensemble des matrices orthogonales d’ordre $n$ .

$O_n(\mathbb{R})$ est un sous-groupe de $(\textrm{GL}_n(\mathbb{R}) ,\, .)$ appelé groupe orthogonal d’ordre $n$ .

$\ast$ Si $M \in O_n(\mathbb{R})$ , $\det M = \pm 1$ .

$\ast$ $\{ U \in O_n(\mathbb{R}) \, / \, \textrm{det}(U) = 1\}$ est un sous-groupe de $O_n(\mathbb{R})$ noté $SO_n(\mathbb{R})$ et appelé groupe spécial orthogonal d’ordre $n$ .

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

Avis Google France ★★★★★ 4,9 sur 5

D. Symétries orthogonales en Maths Sup

$E$ est un espace euclidien.

4.1. Caractérisation des symétries orthogonales en Maths Sup

Si $s$ est une symétrie de $E$ , on dit que $s$ est une symétrie orthogonale lorsque $s$ vérifie les conditions équivalentes :

$\ast$ $\forall\, a \in \textrm{Ker}(s - \textrm{Id} _E)$ , $\forall\, b \in \textrm{Ker}(s + \textrm{Id} _E)$ , $(a \mid b) = 0$

$\ast$ $\textrm{Ker}(s -\textrm{Id} _E) = \left ( \textrm{Ker}(s + \textrm{Id} _E) \right ) ^{\perp}$

$\ast$ $\textrm{Ker}(s + \textrm{Id} _E) = \left ( \textrm{Ker}(s - \textrm{Id} _E) \right ) ^{\perp}$

$\bullet$ Si $s$ est une symétrie de $E$ , $s$ est une symétrie orthogonale ssi $s$ est une isométrie.

2. Réflexion de symétries orthogonales en Maths Sup

$\bullet$ Une symétrie orthogonale est une réflexion lorsque $\textrm{Ker} (s - \textrm{Id}_E)$ est un hyperplan $H$ de $E$ .

On dit que $s$ est une réflexion par rapport à l’hyperplan $H$

$\bullet$ Si $s$ est une réflexion par rapport à $H$ et si $u$ est un vecteur normal unitaire à $H$ , $\forall\, x \in E, \, s(x) = x - \displaystyle 2\, {(u \mid x)} \, u$ .

E. Produit mixte en Maths Sup

On suppose que $E$ est un espace euclidien.

$\bullet$ On suppose dans la suite que l’espace euclidien est orienté, on a donc choisi une base $\mathcal{B}$ dite directe.

Toutes les bases $\mathcal{C}$ telles que $\det _ {\mathcal{B}} \mathcal{C} > 0$ sont aussi directes, celles telles que $\det _ {\mathcal{B}} \mathcal{C} < 0$ sont dites indirectes.

$\bullet$ Si $\mathcal{B}$ et $\mathcal{C}$ sont deux bases orthonormales directes, la matrice de passage de $\mathcal{B}$ à $\mathcal{C}$ est une matrice orthogonale de déterminant égal à 1.

Dans la suite, $E$ est un espace euclidien orienté de dimension $n$ .

$\bullet$ Le déterminant de $n$ vecteurs de $E$ dans une base orthonormale directe ne dépend pas de la base orthonormale directe choisie pour le calculer.

On l’appelle produit mixte de ces $n$ vecteurs et on le note $[x_1\, ,\, \cdots \, , \, x_n]$ .

$\bullet$ Le produit mixte est une forme $n$ -linéaire alternée.

$\bullet$ Pour $n = 2$ , $\vert \, [u \, , \, v] \, \vert$ s’interprète comme l’aire du parallélogramme construit sur les vecteurs $u$ et $v$ .

$\bullet$ Pour $n = 3$ , $\vert \, [u \, , \, v,\, w ] \, \vert$ s’interprète comme le volume du parallélépipède construit sur les vecteurs $u$ , $v$ et $w$ .

F. Matrices orthogonales d’ordre 2

P1 : Toute matrice de $O_2(\mathbb{R})$ s’écrit

$\ast$ $R(t) = \begin{pmatrix} \cos t & - \sin t \\ \sin t & \cos t \end{pmatrix}$ si son déterminant est égal à $1$ .

$\ast$ $S(t) = \begin{pmatrix} \cos t & \sin t \\ \sin t & -\cos t \end{pmatrix}$ si son déterminant est égal à $-1$ .

P2 : $\ast$ $(SO_2(\mathbb{R})\, ,\, .)$ est un groupe commutatif.

Pour tout $(t , \, t') \in \mathbb{R}^2$ ,

$\ast$ $R(t) R(t') = R(t + t') = R(t') R(t)$ et $R(t) ^{-1} = R(-t)$ .

$\ast$ $S(t) S(t') = R(t - t')$ .

P3 : Soit $E$ un plan euclidien orienté et $r \in SO(E)$ , il existe un unique réel $t$ de $]- \pi,\, \pi]$ tel que la matrice de $r$ dans toute base orthonormale directe de $E$ s’écrive $R(t)$ .

On dit que $r$ est une rotation d’angle de mesure $t$ .

P4 : Si $r$ est une rotation du plan euclidien orienté $E$ , on détermine une mesure de l’angle $t$ de la rotation $r$ en introduisant un vecteur unitaire $u$ et en résolvant

$\quad \cos t = (u \, | \, v)$

et $\sin t = [u \, , \, v]$ ( $[u \, ,\, v]$ est le produit mixte de $u$ et $v$ défini dans le §4).

P5 : Si $s$ est une isométrie du plan euclidien $E$ de déterminant égal à $- 1$ , il existe un réel $t$ tel que la matrice de $s$ dans une base orthonormale soit $S(t)$ . $s$ est alors la réflexion par rapport à la droite $\textrm{Vect}(a)$ où $a$ est un vecteur directeur de la droite $\textrm{Ker} (s - \textrm{Id}_E).$

Si certaines difficultés refont surface dans ce cours, il est important d’y remédier en s’exerçant régulièrement sur plusieurs exercices, notamment sur les exercices de cours en ligne en Maths Sup. D’autres chapitres peuvent également être retravaillés pour se perfectionner :

Les espaces euclidiens en Maths Sup MPSI, MP2I, PCSI, PTSI

A. Espace vectoriel euclidien $E$ en Maths Sup

1. Base orthonormale d’un espace euclidien $E$

2. Supplémentaire orthogonal en Maths Sup

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour
réussir sa scolarité

En ligne ou à domicile

B. Hyperplans et hyperplans affines en Maths Sup

1. Hyperplans en Maths Sup

2. Hyperplans affines en Maths Sup

C. Caractérisation des isométries et des matrices orthogonales

1. Isométries en Maths Sup

2. Matrices orthogonales en Maths Sup

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension
clés de la réussite

Cours de maths en ligne ou à domicile

D. Symétries orthogonales en Maths Sup

4.1. Caractérisation des symétries orthogonales en Maths Sup

2. Réflexion de symétries orthogonales en Maths Sup

E. Produit mixte en Maths Sup

F. Matrices orthogonales d’ordre 2

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Les espaces euclidiens en Maths Sup MPSI, MP2I, PCSI, PTSI

2. Supplémentaire orthogonal en Maths Sup

COURS DE MATHS A DOMICILE

Les meilleurs profs de maths pour réussir sa scolarité

En ligne ou à domicile

B. Hyperplans et hyperplans affines en Maths Sup

1. Hyperplans en Maths Sup

2. Hyperplans affines en Maths Sup

C. Caractérisation des isométries et des matrices orthogonales

1. Isométries en Maths Sup

2. Matrices orthogonales en Maths Sup

UN PROF DE MATHS POUR EXCELLER

La pratique et la compréhension clés de la réussite

Cours de maths en ligne ou à domicile

D. Symétries orthogonales en Maths Sup

4.1. Caractérisation des symétries orthogonales en Maths Sup

2. Réflexion de symétries orthogonales en Maths Sup

E. Produit mixte en Maths Sup

F. Matrices orthogonales d’ordre 2

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales

Les meilleurs profs de maths pour
réussir sa scolarité

La pratique et la compréhension
clés de la réussite