Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur l’Analyse Asymptotique en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Les équivalents
1. Exercices : 3 applications directes des équivalents usuels
2. Exercices : 7 équivalents illustrant les méthodes
3. Exercices : 7 équivalents à choisir parmi des propositions
4. Les équivalents et la fonction ![]()
5. On demande des exemples
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Exercice 1 : Justifier ces résultats en analyse asymptotique
1) ![]()
Correction : On sait que ![]() et ch admet 1 pour limite en 0, donc
et ch admet 1 pour limite en 0, donc ![]()
et enfin ![]() par un équivalent usuel ou le DL de ch à l’ordre 2 en 0.
par un équivalent usuel ou le DL de ch à l’ordre 2 en 0.
2) ![]()
Correction : en utilisant ![]()
![]() .
.
Comme ![]() ,
,
![]()
(Méthodes M3 du paragraphe 8)
3) ![]()
Correction :
![]() donc
donc ![]()
En utilisant ![]() ,
,
![]()
![]()
et ![]()
Donc ![]() .
.
(Méthodes M3 du paragraphe 4).
Exercice 2 : Donner un équivalent au voisinage de  de
de
1) ![]() pour
pour ![]()
Correction :
En effet en notant ![]() , on cherche un équivalent de
, on cherche un équivalent de ![]() ,
,
la fonction ![]() est dérivable en e et de dérivée non nulle égale à 1/e ,
est dérivable en e et de dérivée non nulle égale à 1/e , ![]()
![]() .
.
(Méthodes M2 du paragraphe 8)
2) ![]() pour
pour ![]() où
où ![]() est entier.
est entier.
Correction :
attention, on ne suppose pas ![]() ,
, ![]()
car ![]() et
et ![]() tend vers 0.
tend vers 0.
Il faut savoir que si ![]() ,
, ![]()
(considérer les cas ![]() pair puis
pair puis ![]() impair).
impair).
3) ![]() pour
pour ![]()
Correction : C’est une expression de la forme ![]() avec
avec ![]() dérivable en
dérivable en ![]() de dérivée non nulle égale à 2
de dérivée non nulle égale à 2
![]()
![]()
(Méthodes M2 du § 8).
4) ![]() où
où ![]() et
et ![]() ,
, ![]()
Correction : ![]()
car ![]()
![]() est dérivable en
est dérivable en ![]() de dérivée
de dérivée
![]() non nulle
non nulle
(on avait à trouver un équivalent de ![]() voir Méthodes M2 du paragraphe 8).
voir Méthodes M2 du paragraphe 8).
5) ![]() ,
, ![]()
Correction :
![]()
![]()
![]()
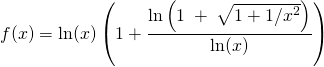
et 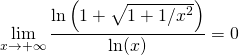 . (Méthodes M3 du §8).
. (Méthodes M3 du §8).
⚠️ Si vous avez répondu ![]() , êtes vous sûr de ne pas avoir fait une somme d’équivalents puis une composition par la fonction
, êtes vous sûr de ne pas avoir fait une somme d’équivalents puis une composition par la fonction ![]() ?
?
On peut néanmoins démontrer que ![]() est équivalent à
est équivalent à ![]() en
en ![]() .
.
6) ![]() ,
, ![]()
Correction : ![]() .
.
Soit ![]() .
.
Comme ![]() , et
, et ![]() ,
, ![]()
![]()
avec ![]() (Méthodes M1 du §8)
(Méthodes M1 du §8)
7) ![]() et
et ![]() ,
, ![]()
8) ![]() ,
, ![]()
9) ![]() ,
, ![]()
10) ![]() ,
, 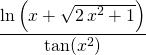
11) ![]() ,
, ![]()
12) ![]() ,
, ![]()
Exercice 3 : Trouver un équivalent en  des fonctions suivantes
des fonctions suivantes
1) ![]() et
et ![]() ,
, ![]()
2) ![]() et
et ![]() ,
, ![]()
3) ![]() et
et ![]() ,
, ![]()
4) ![]() ,
, ![]()
5) ![]() ,
, ![]()
6) ![]() ,
, ![]()
7) ![]() ,
, ![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Les équivalents et la fonction 
On suppose que ![]() et
et ![]() sont à valeurs strictement positives et que
sont à valeurs strictement positives et que ![]() .
.
Question 1
Si ![]() , montrer que
, montrer que ![]() .
.
Question 2
Si ![]() , montrer que
, montrer que ![]()
5. On demande des exemples
Trouver des exemples de fonctions remplissant les conditions suivantes :
1) ![]() ,
, ![]() et
et ![]() sont à valeurs strictement positives et
sont à valeurs strictement positives et ![]() n’est pas équivalent à
n’est pas équivalent à ![]() en
en ![]() .
.
2) ![]() et
et ![]() n’est pas équivalent à
n’est pas équivalent à ![]() en
en ![]() .
.
3) ![]() ,
, ![]() et
et ![]() sont à valeurs strictement positives et
sont à valeurs strictement positives et ![]() n’est pas équivalent à
n’est pas équivalent à ![]() en
en ![]() .
.
4) ![]() ,
, ![]() est à valeurs strictement positives et
est à valeurs strictement positives et ![]() n’est pas équivalent à
n’est pas équivalent à ![]() en
en ![]() .
.
5) Trouver deux suites équivalentes ![]() et
et ![]() , telles que les suites
, telles que les suites ![]() et
et ![]() ne le soient pas
ne le soient pas
Les exercices des cours en ligne sont des exercices typiques de cours. L’entraînement sur ces cours en ligne de Maths en MPSI, PCSI et PTSI ne pourra que vous être bénéfique et pourra vous faire progresser durablement. Pour continuer à garder un bon niveau, entraînez-vous aussi sur les divers chapitres au programme :

