Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés d’arithmétique en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices :
1. Divisibiité
2. Sur les nombres premiers
3. PGCD
4. Produit des diviseurs
5. Somme des diviseurs
6. Nombres de Mersenne
7. Nombres de Fermat
8. Triangles Pythagoriciens
9. Théorème de Wilson
10. Théorème chinois
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Divisibilité
Exercice 1 : arithmétique maths sup
![]() ,
, ![]() divise
divise ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
Deux démonstrations sont proposées.
![]() On raisonne avec la relation de congruence modulo 7.
On raisonne avec la relation de congruence modulo 7.
![]()
![]()
donc ![]()
soit ![]()
et 7 divise ![]() .
.
![]() Démonstration par récurrence.
Démonstration par récurrence.
Si ![]() , on note
, on note
![]() divise
divise ![]() .
.
![]() Pour
Pour ![]() ,
, ![]() est divisible par 7.
est divisible par 7.
![]() On suppose que
On suppose que ![]() est vraie, il existe donc
est vraie, il existe donc ![]() tel que
tel que ![]() .
.
![]()
![]()
![]()
![]()
![]() est divisible par 7.
est divisible par 7.
Donc ![]() est vraie.
est vraie.
La propriété est démontrée par récurrence.
Exercice 2
![]() ,
, ![]() divise
divise ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
![]() On utilise les relations de congruence modulo 7 et 5.
On utilise les relations de congruence modulo 7 et 5.
![]()
![]()
donc ![]()
soit ![]()
ce qui donne ![]() divise
divise ![]() .
.
![]()
![]()
donc ![]()
puis ![]()
donc ![]()
soit ![]()
et alors ![]()
On obtient : ![]()
ce qui donne ![]() divise
divise ![]() .
.
Comme ![]() ,
, ![]() divise
divise ![]() .
.
![]() Autre méthode.
Autre méthode.
On suppose que ![]() car
car ![]() .
.
On rappelle que si ![]() ,
, 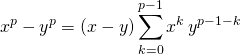 .
.
![]()
avec ![]() et
et ![]()
![]() où
où 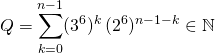
![]() .
.
On peut remarquer que cette méthode prouve même que ![]() est divisible par
est divisible par ![]() .
.
Exercice 3
Si ![]() ,
, ![]() divise
divise ![]() Vrai ou Faux ?
Vrai ou Faux ?
Correction : Par le binôme de Newton,
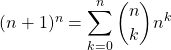
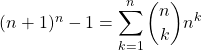
![]()
![]()
![]() Si
Si ![]() ,
, ![]() divise
divise ![]() , donc
, donc ![]() .
.
alors ![]()
et ![]() divise
divise ![]() .
.
Exercice 4
Soient ![]() et
et ![]() deux éléments de
deux éléments de ![]()
Il y a équivalence entre
1) ![]() divise
divise ![]() et
et ![]()
2) ![]() est un multiple de
est un multiple de ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
![]() Si
Si ![]() divise
divise ![]() et
et ![]() ,
, ![]() divise
divise ![]() et
et ![]() , donc divise
, donc divise ![]() .
.
![]() On démontre la contraposée.
On démontre la contraposée.
On suppose que ![]() ne divise pas
ne divise pas ![]() ou
ou ![]() .
.
On peut se ramener au cas où ![]() ne divise pas
ne divise pas ![]() .
.
On utilise la relation de congruence modulo 7.
![]()
![]()
![]()
![]() ou
ou ![]()
![]()
![]()
![]() ou
ou ![]()
![]()
![]()
![]() ou
ou ![]()
![]()
![]() est congru modulo 7 à
est congru modulo 7 à ![]() ,
, ![]() ou
ou ![]() .
.
![]() est congru modulo 7 à
est congru modulo 7 à ![]() ,
, ![]() ,
, ![]() ou
ou ![]() .
.
Donc ![]() est congru modulo 7 à la somme des congruences soit à
est congru modulo 7 à la somme des congruences soit à ![]() , avec
, avec ![]() , il n’est jamais congru à 0 donc
, il n’est jamais congru à 0 donc ![]() ne divise pas
ne divise pas ![]() .
.
2. Sur les nombres premiers
Exercice 1
![]() est un irrationnel. Vrai ou Faux ?
est un irrationnel. Vrai ou Faux ?
Correction : On suppose qu’il existe ![]() tels que
tels que ![]()
![]()
![]()
![]()
alors ![]()
![]()
![]()
donc ![]() donnerait
donnerait ![]() divise
divise ![]() ce qui est absurde.
ce qui est absurde.
![]() est un irrationnel.
est un irrationnel.
Exercice 2
Soit ![]() un nombre premier impair tel que
un nombre premier impair tel que ![]() divise
divise ![]() où
où ![]() .
.
![]() .
.
Vrai ou Faux ?
Correction : ![]() divise
divise ![]() donc
donc ![]() .
.
![]() est impair, on l’écrit
est impair, on l’écrit ![]() avec
avec ![]() car
car ![]() .
.
![]() divise
divise ![]()
![]()
![]() ne divise pas
ne divise pas ![]() (car si
(car si ![]() ,
, ![]() , donc
, donc ![]() divise 1, ce qui est impossible).
divise 1, ce qui est impossible).
Par le petit théorème de Fermat : ![]()
or ![]()
![]()
![]()
donc ![]() .
.
![]() et
et ![]() divise
divise ![]() donc
donc ![]() alors
alors ![]() .
.
On a écrit ![]() donc
donc ![]() .
.
Exercice 3
Il existe une infinité de nombres premiers de la forme ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : On raisonne par l’absurde en supposant qu’il n’y en a qu’un nombre fini d’entiers de la forme ![]() pour
pour ![]()
![]() car
car ![]() et
et ![]() sont premiers et de la forme
sont premiers et de la forme ![]() .
.
On note ![]() et
et ![]()
![]() est de la forme
est de la forme ![]() où
où ![]() .
.
Si ![]() est un nombre premier divisant
est un nombre premier divisant ![]() , il est impair. Il divise
, il est impair. Il divise ![]()
alors ![]() est de la forme
est de la forme ![]() d’après l’exercice 2 qui précède.
d’après l’exercice 2 qui précède.
S’il existait ![]() tel que
tel que ![]() , alors
, alors ![]() divise
divise ![]() et
et ![]() donc
donc ![]() divise 1, ce qui est impossible.
divise 1, ce qui est impossible.
On a prouvé un nombre premier ![]() de la forme
de la forme ![]() différent des
différent des ![]() pour
pour ![]() .
.
Il y a donc une infinité de nombres premiers de la forme ![]() .
.
3. PGCD
Exercice 1
Soit ![]() .
.
a) Le pgcd de ![]() et
et ![]()
b) Le pgcd de ![]() et
et ![]()
Exercice 2
Résoudre l’équation ![]() dans
dans ![]() .
.
Exercice 3
Résoudre : ![]() .
.
Exercice 4
Déterminer les entiers naturels ![]() et
et ![]() ayant respectivement 21 et 10 divi- seurs dans
ayant respectivement 21 et 10 divi- seurs dans ![]() tels que
tels que ![]()
Exercice 5
Résoudre dans ![]()
![]()
Exercice 6
Résoudre dans ![]()
![]()
4. Produits des diviseurs
Soit ![]() un entier de décomposition primaire
un entier de décomposition primaire 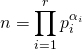 .
.
Question 1
Quel est le nombre ![]() de diviseurs dans
de diviseurs dans ![]() de
de ![]() ?
?
Correction :
![]() divise
divise ![]() ssi sa décomposition primaire
ssi sa décomposition primaire ![]() vérifie
vérifie
![]() .
.
Avec les notations de l’énoncé, ![]() divise
divise ![]() ssi
ssi 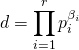 avec
avec ![]() pour
pour ![]() .
.
Le nombre de diviseurs dans ![]() de
de ![]() est égal au nombre d’éléments de l’ensemble
est égal au nombre d’éléments de l’ensemble ![Rendered by QuickLaTeX.com \displaystyle \prod _ {i = 1} ^r [[ 0 \,,\, \alpha_i]] \;](https://groupe-reussite.fr/ressources/wp-content/ql-cache/quicklatex.com-606cfe2f1802fa33304978fc6d5cdc16_l3.png) ,
, 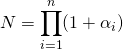 .
.
Question 2
Calculer ![]() .
.
Correction :
On note ![]() .
.
![]() est une bijection, donc
est une bijection, donc ![]()
et par produit
![]()
où ![]() est le nombre de diviseurs de
est le nombre de diviseurs de ![]() que l’on a calculé dans la première question :
que l’on a calculé dans la première question : 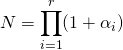 .
.
Alors ![]() .
.
Question 3
Déterminer l’ensemble des entiers ![]() tels que
tels que ![]() .
.
Correction : On note ![]() le nombre de diviseurs dans
le nombre de diviseurs dans ![]() de
de ![]() .
.
![]() ssi
ssi ![]()
ssi ![]() ssi
ssi ![]()
ssi 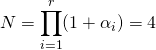 .
.
Si ![]() ,
, 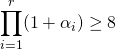 car
car ![]()
donc ![]() .
.
![]() Si
Si ![]() , on obtient la CNS :
, on obtient la CNS : ![]() .
.
Ce qui donne la CNS : ![]() .
.
![]() Si
Si ![]() , on obtient la CNS :
, on obtient la CNS : ![]()
ssi ![]()
ssi ![]() ,
, ![]() tel que
tel que ![]() .
.
En résumé, l’ensemble des solutions est l’ensemble des entiers tels que
![]()
ou ![]() ,
, ![]() tel que
tel que ![]() .
.
Question 4
Déterminer ![]() tel que
tel que ![]()
Correction : On cherche la décomposition primaire de ![]() .
.
Les seuls diviseurs premiers de ![]() sont
sont ![]() et
et ![]() .
.
On écrit ![]() et
et ![]()
Par le calcul précédent,
![]()
ce qui donne ![]() et
et ![]()
donc par quotient ![]() .
.
On résout ![]() ssi
ssi
![]()
alors ![]()
![]() ou
ou ![]() .
.
![]() n’est pas solution.
n’est pas solution.
![]() est solution.
est solution.
Puis ![]() , donc
, donc ![]() .
.
On peut vérifier puisque le raisonnement n’a pas été fait par équivalence que ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
5. Somme des diviseurs
Si ![]() , on note
, on note ![]()
et ![]() .
.
Question 1
Calculer ![]() lorsque
lorsque ![]() et
et ![]() .
.
Correction :![]() .
.
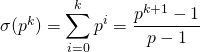 .
.
Question 2
Si ![]() et
et ![]() , montrer que
, montrer que ![]()
Correction :
On définit
![]()
![]() .
.
![]() Il est évident que si
Il est évident que si ![]() divise
divise ![]() et
et ![]() divise
divise ![]() ,
, ![]() divise
divise ![]() , donc
, donc ![]() est à valeurs dans
est à valeurs dans ![]() .
.
![]() On démontre que
On démontre que ![]() est surjective.
est surjective.
Soit ![]() .
.
Si ![]()
soit ![]() .
.
Comme ![]()
Donc si ![]() est un diviseur premier de
est un diviseur premier de ![]() ,
, ![]() est un diviseur de
est un diviseur de ![]() ou un diviseur de
ou un diviseur de ![]() mais n’est pas un diviseur des deux.
mais n’est pas un diviseur des deux.
En regroupant dans ![]() les facteurs tels que
les facteurs tels que ![]() et dans
et dans ![]() ceux tels que
ceux tels que ![]() , on peut écrire
, on peut écrire ![]() avec
avec ![]() et
et ![]() .
.
On a écrit ![]()
![]() On démontre que
On démontre que ![]() est injective.
est injective.
Si ![]() avec
avec ![]() et
et ![]() ,
,
![]() divise
divise ![]() et
et ![]() car
car ![]() , donc
, donc ![]() divise
divise ![]() .
.
En échangeant ![]() et
et ![]() ,
, ![]() divise
divise ![]() . Comme ils sont dans
. Comme ils sont dans ![]() ,
, ![]() , donc
, donc ![]() .
.
On a donc prouvé que l’application ![]()
![]()
est une bijection.
Alors ![]()
![]()
soit ![]() .
.
Question 3
Calculer ![]() lorsque la décomposi- tion primaire de
lorsque la décomposi- tion primaire de ![]() est
est 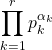 .
.
Correction : ![]() Si
Si ![]() , on note
, on note
![]() : si les entiers
: si les entiers ![]() (où
(où ![]() ) sont deux à deux premiers entre eux,
) sont deux à deux premiers entre eux, ![]() .
.
![]()
![]() est évidente.
est évidente.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
Si les entiers ![]() (où
(où ![]() ) sont deux à deux premiers entre eux, les entiers
) sont deux à deux premiers entre eux, les entiers ![]() et
et ![]() sont premiers entre eux (un diviseur premier de
sont premiers entre eux (un diviseur premier de ![]() ne peut être un diviseur de
ne peut être un diviseur de ![]() ), donc par la question 2,
), donc par la question 2,
![]()
ce qui donne ![]() en utilisant
en utilisant ![]() pour exprimer
pour exprimer ![]() .
.
La propriété est démontré par récurrence.
![]() En utilisant le résultat précédent avec si
En utilisant le résultat précédent avec si ![]() ,
, ![]() qui sont
qui sont ![]() entiers 2 à 2 premiers entre eux,
entiers 2 à 2 premiers entre eux,
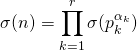
puis on termine avec la question 1
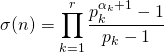 .
.
Question 4
Un entier ![]() est dit parfait lorsque
est dit parfait lorsque ![]() (soit lorsque la somme des diviseurs stricts de
(soit lorsque la somme des diviseurs stricts de ![]() est égal à
est égal à ![]() ).
).
On suppose que ![]() est premier. Montrer que
est premier. Montrer que ![]() est un nombre parfait.
est un nombre parfait.
Donner 3 exemples de nombres parfaits
Correction :
![]() admet deux facteurs premiers
admet deux facteurs premiers ![]() et
et ![]() (
(![]() car
car ![]() ) donc
) donc
![]()
![]() .
.
Donc ![]() est un entier parfait.
est un entier parfait.
![]() Si
Si ![]() ,
, ![]() est premier donc
est premier donc ![]() est un nombre parfait
est un nombre parfait
![]() Si
Si ![]() ,
, ![]() est premier donc 24 est un nombre parfait
est premier donc 24 est un nombre parfait
![]() Si
Si ![]() ,
, ![]() n’est pas premier
n’est pas premier
![]() Si
Si ![]() ,
, ![]() est premier donc
est premier donc ![]() est parfait.
est parfait.
6, 24 et 496 sont des entiers parfaits.
6. Nombres de Mersenne
Le ![]() -ième nombre de Mersenne où
-ième nombre de Mersenne où ![]() est défini par
est défini par ![]() .
.
Question 1
Si ![]() et
et ![]() est premier,
est premier, ![]() est impair. Vrai ou Faux.
est impair. Vrai ou Faux.
Correction : En effet si ![]() avec
avec ![]() et
et ![]() , en notant
, en notant ![]() ,
,
![]()
![]()
![]()
![]() et
et ![]() , on a prouvé que
, on a prouvé que ![]() n’est pas premier.
n’est pas premier.
Par contraposée, si ![]() et
et ![]() est premier,
est premier, ![]() est impair.
est impair.
Question 2
Si ![]() est premier,
est premier, ![]() est premier. Vrai ou Faux ?
est premier. Vrai ou Faux ?
Correction :
On suppose que ![]() avec
avec ![]() et
et ![]() .
.
![]()
avec 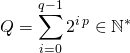
![]() est un diviseur de
est un diviseur de ![]() différent de
différent de ![]() et de
et de ![]() .
.
Donc ![]() n’est pas premier.
n’est pas premier.
De même ![]() divise
divise ![]() .
.
![]() ,
, ![]() et
et ![]() sont premiers
sont premiers
![]() n’est pas premier alors que
n’est pas premier alors que ![]() l’est.
l’est.
Question 3
Si ![]() ,
, ![]() .
.
7. Nombres de Fermat
Question 1
Si ![]() est impair au moins égal à 3,
est impair au moins égal à 3, ![]() n’est pas premier. Vrai ou Faux ?
n’est pas premier. Vrai ou Faux ?
Correction :
![]() Première méthode
Première méthode
Si ![]() , on note
, on note ![]()
![]() Pour
Pour ![]() ,
, ![]()
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
donc ![]() est vraie.
est vraie.
La propriété est vraie par récurrence.
Pour tout ![]() donc
donc ![]() est divisible par 3 et au moins égal à 9, donc n’est pas premier.
est divisible par 3 et au moins égal à 9, donc n’est pas premier.
![]() Deuxième méthode
Deuxième méthode
On peut aussi écrire
Si ![]() est impair et différent de
est impair et différent de ![]() ,
, ![]() ,
,
![]()
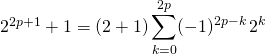
où 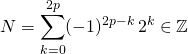 et
et ![]() , 3 est un diviseur strict,
, 3 est un diviseur strict,
donc ![]() n’est pas premier.
n’est pas premier.
![]() Troisième méthode
Troisième méthode
![]() est premier et
est premier et ![]() ,
,
par le théorème de Fermat, ![]()
donc ![]()
soit ![]()
![]() divise
divise ![]() et
et ![]() .
.
Donc ![]() n’est pas premier.
n’est pas premier.
Question 2
Si ![]() avec
avec ![]() ,
, ![]() n’est pas premier. Vrai ou Faux ?
n’est pas premier. Vrai ou Faux ?
Correction : On note ![]() et
et ![]()
![]()
donc ![]() avec
avec 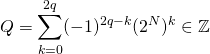
et ![]() .
.
Donc ![]() est un diviseur strict de
est un diviseur strict de ![]() , qui n’est pas premier.
, qui n’est pas premier.
Si ![]()
![]() désigne le
désigne le ![]() -ième entier de Fermat.
-ième entier de Fermat.
On peut remarquer que
![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() sont premiers
sont premiers
![]() n’est pas premier.
n’est pas premier.
Question 3
Si ![]() ,
, ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Si ![]() , on note
, on note ![]() .
.
![]() est vraie car
est vraie car ![]() .
.
On suppose que ![]() est vraie.
est vraie.
![]()
![]()
par la factorisation de ![]() ,
,
![]()
En utilisant l’hypothèse de récurrence :
![]() .
.
ce qui donne ![]() .
.
La propriété est démontrée par récurrence.
Question 4
Si ![]() ,
, ![]() .
.
8. Triangles pythagoriciens
On veut résoudre dans ![]() l’équation
l’équation ![]()
(de tels triplets d’entiers relatifs sont appelés triplets pythagoriciens).
On cherche dans la suite les triplets différents de la solution triviale comme par exemple ![]() .
.
Dans les questions ![]() à
à ![]() , on suppose que
, on suppose que ![]() est une solution non triviale de l’équation.
est une solution non triviale de l’équation.
Question 1
Montrer que l’on peut se ramener au cas où ![]() . Montrer que, dans ce cas,
. Montrer que, dans ce cas, ![]() ,
, ![]() et
et ![]() sont de plus deux à deux premiers entre eux.
sont de plus deux à deux premiers entre eux.
Correction : ![]() Soient
Soient ![]() solutions de
solutions de ![]() .
.
On note ![]() .
.
![]() sinon
sinon ![]() , cas exclu dans cette étude.
, cas exclu dans cette étude.
Alors ![]() ,
, ![]() et
et ![]() avec
avec ![]() et
et ![]() .
.
![]() On suppose
On suppose ![]() solution et
solution et ![]() .
.
![]() si
si ![]() , en introduisant
, en introduisant ![]() tel que
tel que ![]() divise
divise ![]() ,
, ![]() divise
divise ![]() et
et ![]() donc
donc ![]() divise
divise ![]() , donc
, donc ![]() divise
divise ![]() ce qui contredit
ce qui contredit ![]() .
.
![]() si
si ![]() , en introduisant
, en introduisant ![]() tel que
tel que ![]() divise
divise ![]() ,
, ![]() divise
divise ![]() et
et ![]() donc
donc ![]() divise
divise ![]() , donc
, donc ![]() divise
divise ![]() ce qui contredit
ce qui contredit ![]() .
.
![]() si
si ![]() , en introduisant
, en introduisant ![]() tel que
tel que ![]() divise
divise ![]() ,
, ![]() divise
divise ![]() et
et ![]() donc
donc ![]() divise
divise ![]() , donc
, donc ![]() divise
divise ![]() ce qui contredit
ce qui contredit ![]() .
.
On a prouvé que si ![]() est solution,
est solution, ![]() sont premiers 2 à 2.
sont premiers 2 à 2.
Question 2
On suppose que ![]() et
et ![]() sont deux à deux premiers entre eux. Montrer que deux des trois nombres
sont deux à deux premiers entre eux. Montrer que deux des trois nombres ![]() ,
, ![]() et
et ![]() sont impairs, le troisième étant pair puis que
sont impairs, le troisième étant pair puis que ![]() est impair.
est impair.
Correction :
![]() Il est impossible d’avoir au moins deux entiers pairs car alors ces deux entiers ne seraient pas premiers entre eux.
Il est impossible d’avoir au moins deux entiers pairs car alors ces deux entiers ne seraient pas premiers entre eux.
![]() Il y a au moins deux entiers impairs. La somme ou la différence de deux carrés d’impairs est une somme ou différence de deux nombres impairs donc est paire et alors le carré du troisième est pair, le troisième est pair.
Il y a au moins deux entiers impairs. La somme ou la différence de deux carrés d’impairs est une somme ou différence de deux nombres impairs donc est paire et alors le carré du troisième est pair, le troisième est pair.
![]() si
si ![]() et
et ![]() sont impairs, on les écrit
sont impairs, on les écrit ![]() ,
, ![]() et on écrit
et on écrit ![]() .
.
Donc ![]() donne
donne ![]() ce qui est impossible.
ce qui est impossible.
![]() On en déduit que l’un des deux entiers
On en déduit que l’un des deux entiers ![]() est pair, les autres entiers étant impairs. En particulier
est pair, les autres entiers étant impairs. En particulier ![]() est impair.
est impair.
Par symétrie, on peut supposer que ![]() est pair,
est pair, ![]() et
et ![]() sont impairs.
sont impairs.
On peut donc écrire ![]() et comme
et comme ![]() et
et ![]() sont pairs, on introduit
sont pairs, on introduit ![]() tels que
tels que ![]() et
et ![]() .
.
Question 3
![]() et
et ![]() et
et ![]() sont des carrés parfaits.
sont des carrés parfaits.
Question 4
En déduire que l’ensemble des triplets pythagoriciens non triviaux est l’ensemble des triplets de la forme
![]()
où ![]() et
et ![]() , à une permutation près des deux premières composantes.
, à une permutation près des deux premières composantes.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
9. Théorème de Wilson
Le but est de démontrer que si ![]() ,
,
![]() divise
divise ![]() ssi
ssi ![]() est premier.
est premier.
Question 1
Montrer que si ![]() divise
divise ![]() ,
, ![]() est premier.
est premier.
Correction : ![]() Première méthode
Première méthode
Il existe ![]() tel que
tel que ![]()
donc ![]() traduit par le théorème de Bezout que
traduit par le théorème de Bezout que ![]()
![]() Deuxième méthode
Deuxième méthode
Si ![]() est un diviseur de
est un diviseur de ![]() tel que
tel que ![]() , alors
, alors ![]() divise
divise ![]()
donc ![]() divise
divise ![]()
![]() .
.
On a prouvé que ![]() est premier.
est premier.
Dans la suite, on établit la réciproque.
Question 2
Si ![]() ou 3,
ou 3, ![]() divise
divise ![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction : Si ![]() ,
, ![]() est divisible par
est divisible par ![]()
Si ![]() ,
, ![]() est divisible par 3.
est divisible par 3.
Dans la suite, on suppose que ![]() .
.
Question 3.
Montrer que si ![]() , il existe un unique
, il existe un unique ![]() tel que
tel que ![]() et puis que
et puis que ![]()
Correction :
![]() Si
Si ![]() ,
, ![]() , par le théorème de Bezout, il existe
, par le théorème de Bezout, il existe ![]() tel que
tel que ![]()
et par division euclidienne de ![]() par
par ![]() , on écrit
, on écrit ![]() avec
avec ![]()
donc ![]() ce qui donne
ce qui donne ![]() .
.
Il est impossible que ![]() car on aurait
car on aurait ![]() qui n’est pas congru à 1.
qui n’est pas congru à 1.
Il est impossible que ![]() car on aurait
car on aurait ![]() donc
donc ![]() ce qui contredit
ce qui contredit ![]() .
.
![]()
![]()
![]()
donc ![]() divise
divise ![]() .
.
![]() car
car ![]() est un nombre premier et
est un nombre premier et ![]()
![]() car
car ![]() est un nombre premier et
est un nombre premier et ![]()
donc ![]() car
car ![]() est premier et on aboutit à une contradiction.
est premier et on aboutit à une contradiction.
On a prouvé que ![]() .
.
![]() Il reste à prouver l’unicité
Il reste à prouver l’unicité
si ![]() et
et ![]()
avec ![]() et
et ![]() ,
,
![]() et
et ![]()
donc ![]()
![]() divise
divise ![]() , alors
, alors ![]() car
car ![]() est premier.
est premier.
Question 4.
En déduire que si ![]() est premier et
est premier et ![]() ,
, ![]() divise
divise ![]()
Correction :
Pour tout ![]() , il existe un unique
, il existe un unique ![]() , différent de
, différent de ![]() tel que
tel que ![]() .
.
On regroupe les ![]() éléments de
éléments de ![]() en
en ![]() couples
couples ![]() tels que
tels que ![]() alors
alors
![]()
et ![]()
soit ![]()
ce qui démontre la réciproque.
10. Théorème chinois
Exercice 1
Résoudre ![]() .
.
Exercice 2
Soient ![]() et
et ![]() .
.
Soient ![]() et
et ![]() dans
dans ![]() tels que
tels que ![]() .
.
Question 1
Si ![]() ,
,
![]() et
et ![]() .
.
Question 2
Si ![]() vérifie
vérifie ![]() et
et ![]() alors
alors ![]()
Exercice 3
Soient ![]() et
et ![]() des éléments de
des éléments de ![]() deux à deux distincts.
deux à deux distincts.
On note ![]() et pour tout
et pour tout ![]() ,
, ![]() .
.
Comme ![]() et
et ![]() sont premiers entre eux, soit
sont premiers entre eux, soit ![]() tel que
tel que ![]() .
.
Question 1
Soient ![]() .
.
![]() vérifie
vérifie
![]() ,
, ![]() .
.
Question 2
![]() vérifie
vérifie ![]() ssi
ssi ![]() .
.
Question 3
Appliquer les résultats précédents à la résolution du système :
![]() ,
, ![]() et
et ![]() .
.
Vous devez avoir parfaitement assimilé l’ensemble des chapitres de maths au programme de Maths Sup pour réussir d’une part, à suivre les cours en Maths Spé, mais surtout pour réussir votre dernière année de prépa et évidemment les concours post-prépa. Les cours en ligne de Maths Sup vous fournissent des ressources supplémentaires pour vous aider à améliorer votre niveau. Profitez ainsi de nombreux autres cours de maths en PTSI, PCSI et MPSI :

