Chapitres Maths en MPSI, PCSI, MP2I, PTSI

Exercices corrigés sur l’Arithmétique et Polynômes en Maths Sup

Name: Groupe Réussite: Cours particuliers, stages intensifs de révision
Brand: Groupe Réussite
SKU: Cours Particuliers
Rating: 4.8 (1000 reviews)

Résumé de cours Exercices et corrigés

Cours en ligne de Maths en Maths Sup

Plan des exercices d’Arithmétique et Polynômes

1. Calculs de PGCD

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

Avis Google France ★★★★★ 4,9 sur 5

1. Calculs de PGCD en cours d’arithmétique maths sup

Exercice 1 :

pgcd de $A = n \, \textrm{X} ^{n + 1} - (n + 1) X ^n + 1$ et $B = \textrm{X} ^n - n \, \textrm{X} + (n - 1)$

Correction :

On effectue la division euclidienne de $A$ par $B$
$A = B \, Q + R$ avec $Q = n \, \textrm{X} - n - 1$ et $R = n ^2 (\textrm{X} - 1) ^2$ .

$A \wedge B = B \wedge R$
$B(1) = 1 - n + n - 1 = 0$ et $B'(1) = n - n = 0$ , donc $( \textrm{X} - 1)^2$ divise $B$ .
Alors $B \wedge R = (\textrm{X} - 1) ^2$ .

Exercice 2
Trouver une relation de Bezout pour les polynômes réels $A = \textrm{X}^5 +2\, \textrm{X}^3 + \textrm{X}^2 +2$ et $B = \textrm{X}^4 + \textrm{X}^3 + 3\, \textrm{X}^2 + 2 \, \textrm{X} + 2$

Correction :

$\bullet$ On détermine $A \wedge B$ .
On note $R_0 = A$ et $R_1 = B$
Par divisions euclidiennes successives
$\ast$ $R_0 = R_1 \, Q_1 + R_2$ avec $Q_1 = \textrm{X} - 1$ et $R_2 = 2\, \textrm{X}^2 + 4$ .
$\ast$ $R_1 = R_2 \, Q_2 + R_3$ avec $Q _2 = \displaystyle \frac 1 2 (\textrm{X}^2 + \textrm{X})$ et $R _3 = \textrm{X} ^2 + 2$ .
$\ast$ $R_2 = 2 . R_3 + 0$
$R_3$ est le dernier reste non nul et est unitaire, donc $\textrm{X} ^2 + 2 = A \wedge B$

$\bullet$ Relation de Bezout.
$R _ 3 = R_1 - R_2 \, Q_2 = R_1 - (R_0 -R_1 \, Q_1 )\, Q_2$
et $\textrm{X} ^2 + 2 = U \, A + V \, B$ avec
$U = - Q_2 = \displaystyle - \frac 1 2 (\textrm{X}^2 + \textrm{X})$
et $V =1 + Q_1 \,Q_2 = \displaystyle \frac 1 2 \left ( \textrm{X}^3 - \textrm{X} + 2 \right )$ .

2. une suite de polynômes

On définit la suite de polynômes $(P_n)_n$ par $P_ 0 = 1$ , $P_1 = \textrm{X}$ et $\quad \forall \, n \in \mathbb{N }$ , $P_{n + 2} = \textrm{X} \, P_{n + 1} - P_n$ .
Question 1.
Calculer $P_n ^2 - P_ {n + 1} \, P_{n - 1}$ si $n \in \mathbb{N }^*$ .

Correction :

On note $A _n = P_n ^2 - P_ {n + 1} \, P_{n - 1}\,$ .
$\bullet$ $P_ 2 = \textrm{X} \, P_1 - P_0 = \textrm{X} ^2 - 1$
$A_1 = \textrm{X} ^2 - (\textrm{X} ^2 - 1) = 1$

$\bullet$ $A _{n + 1} = P_{n + 1} ^2 - P_ {n + 2} \, P_{n}$
$A _{n + 1} = P_{n + 1} ^2 - (\textrm{X} \, P_{n + 1} - P_n ) \, P_{n}$
$A _{n + 1} = P_{n + 1} ( P_{n + 1} - \textrm{X} \, P_{n} ) + P_n ^2$
$A _{n + 1} = - P_{n + 1} P_{n - 1} + P_n ^2 = A_n \,$ .

$\bullet$ On obtient une suite constante de premier terme égal à 1.
Donc $\forall\, n \in \mathbb{N}^*, P_n ^2 - P_ {n + 1} \, P_{n - 1} = 1$ .

Question 2
Déterminer si $n \in \mathbb{N}$ , $P_n \wedge P_{n + 1}$

Correction :

On a donc écrit $U \, P_n + V \, P_{n + 1} = 1$ avec $U = P_n$ et $V = - P_{n - 1}\,$ , donc $P_{n + 1} \wedge P_n = 1$ .

3. Exercice 3

Soient $A$ et $B$ deux éléments non nuls de $\mathbb{C} [\textrm{X}]$ .
Il y a équivalence entre
a) $A$ et $B$ ne sont pas premiers entre eux
b) Il existe $U$ et $V$ dans $\mathbb{C} [\textrm{X}]$ non nuls tels que $A \, U + B\, V$ , $\textrm{deg} (V) < \textrm{deg}(A)$ et $\textrm{deg}(U) < \textrm{deg} B$ . Vrai ou faux ?

Correction :

$\bullet$ Si $A$ et $B$ ne sont pas premiers entre eux, $D = A \wedge B$ est de degré au moins égal à 1 et on peut écrire $A = A_1 \, D$ et $B = B_1 \, D$ tels que $A _ 1 \wedge B_1 = 1$ .
Alors $\textrm{deg} (A_1) < \textrm{deg} (A)$ et $\textrm{deg} (B_1) < \textrm{deg} (B)$ .
$B _1 \, A - A _ 1 \, B = A_1 \, B_1 \, D - A _ 1 \, B_1 \, D = 0$
$U = B_1$ et $V = - A_1$ conviennent.

$\bullet$ Si $U$ et $V$ existent vérifiant les conditions de b), on note $D = A \wedge B$ et on peut écrire $A = A_1 \, D$ et $B = B_1 \, D$ tels que $A _ 1 \wedge B_1 = 1$ .
$A \, U + B \, V = 0 \Rightarrow A_ 1 \, U + B _ 1 \, V = 0$ .
donc $A _ 1 \, U = - B _ 1 \, V$ et $A _ 1 \wedge B _ 1 = 1$ donnent par le théorème de Gauss, $A _ 1$ divise $V$ .
On peut écrire $V = A _ 1 \,$ donc $\textrm{deg} A_1 \leq \textrm{deg} V \leq \textrm{deg} A$ , donc $\textrm{deg} D \geq 1$ et $A$ et $B$ ne sont pas premiers entre eux.

4. Reste d’une division euclidienne

Soit $a \in \mathbb{C}$ , $p$ et $n$ des entiers tels que $0 < p < n$ .
On note $n = p\, q + r$ avec $0 \leq r < p$
Le reste de la division de $\textrm{X}^n$ par $\textrm{X}^p - a$ est $a^q \,\textrm{X}^r$ . Vrai ou Faux ?

Correction :

$q \in \mathbb{N}^*$ car $n > p$ .
$\textrm{X}^n - a^q \,\textrm{X}^r = \textrm{X}^r \left ( X ^{p \, q} - a^q \right )$
$\textrm{X} ^{p \, q} - a^q = (\textrm{X} ^p) ^q - a ^q$
ce qui donne
$\quad \quad \textrm{X} ^{p \, q} - a^q = (\textrm{X} ^p - a ) \, U$
avec $U = \displaystyle \sum _ {i = 0} ^{q - 1 } a^{q - i - 1} \, (\textrm{X} ^p) ^i$

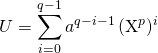
On peut donc écrire
$\textrm{X}^n - a^q \,\textrm{X}^r = \textrm{X}^r ( \textrm{X} ^p - a) \, U$
et alors
$\textrm{X}^n = ( \textrm{X} ^p - a) \textrm{X}^r \, U + a^q \,\textrm{X}^r$
ce qui donne par unicité de la division euclidienne que le reste est égal à $a^q \,\textrm{X}^r$

5. Détermination d’un pgcd

Soit $a \in \mathbb{C}$ , $p$ et $n$ des entiers tels que $0 < p < n$ .
Question 1
On note $n = p \,q + r$ avec $0 \leq r < p$
$(\textrm{X}^n - a^n) \wedge (\textrm{X}^p - a^p) =$ $\quad \quad \quad \quad (\textrm{X}^p - a^p) \wedge (\textrm{X}^r - a^r)$

Correction :

$\textrm{X}^n - a^n = \textrm{X}^{p q} \, \textrm{X}^{r} - a^{p\, q} \, a^r$
$\textrm{X}^n - a^n =$ $\quad \textrm{X}^{r} \left ( \textrm{X}^{p q} - a^{p\, q}\right ) + a^{p\, q} \left ( \textrm{X}^{r} - a ^r \right )$

puis $\textrm{X}^{p \, q} - a^{p\, q} = (\textrm{X}^{p }) ^q - (a^{p}) ^q$
$\textrm{X}^{p \, q} - a^{p\, q} = (\textrm{X}^{p }- a^{p}) \, U$
avec $U = \displaystyle \sum _ {k = 0} ^{q - 1} (a ^p) ^{q - 1 - k} \, \textrm{X}^{p \, i }$

$\textrm{X}^n - a^n = (\textrm{X}^{p }- a^{p}) \, U \, \textrm{X}^{r} + a^{p\, q} \left ( \textrm{X}^{r} - a ^r \right )$
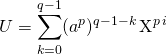
On a donc prouvé que le reste de la division de $\textrm{X}^n - a^n$ par $\textrm{X}^{p }- a^{p}$ est égal à $\textrm{X}^{r} - a ^r$
donc
$(\textrm{X}^n - a^n) \wedge (\textrm{X}^p - a^p) =$ $\quad \quad \quad \quad (\textrm{X}^p - a^p) \wedge (\textrm{X}^r - a^r)$

Question 2
Soit $\delta = n \wedge p$ .
$(\textrm{X}^n - a^n) \wedge (\textrm{X}^p - a^p) = \textrm{X}^{\delta} - a^{\delta}$ .

Vrai ou Faux ?

Correction :

Dans la suite on note $A _ k = \textrm{X}^k - a^k$ .

On note $n_0 = n$ et $n _ 1 = p$ et on utilise l’algorithme d’Euclide avec les entiers $n_0$ et $n_ 1\,$ .
On écrit $n _ 0 = n _ 1 \ q_1 + n _ 2$ , on sait que $\delta$ est le dernier reste non nul $n _ {k + 1}$ dans la suite des divisions de $n _ 0$ par $n -1$ , de $n - 1$ par $n_ 2$ etc …

En utilisant $A_{n _0} \wedge A_{n _ 1} = A_{n _1} \wedge A_{n _ 2}= ... =$
$A_n \wedge A_p = A_{n _k} \wedge A_{n _ {k + 1}}\,$ .
Et comme $n _ k = q _ k \, n _ {k + 1}$ , $\quad \quad A_{n _k} \wedge A_{n _ {k + 1}} = A_{n _ {k + 1}}\,$ car le reste de la division est nul.

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

Avis Google France ★★★★★ 4,9 sur 5

6. Théorème de Bezout précisé

Soit $(A , B) \in ( \mathbb{K} [\textrm{X}] \setminus \{0\}) ^2$ tel que $A \wedge B = 1$ .
On note $n = \max (\textrm {deg} \, A , \textrm {deg} \, B)$
Il existe un unique couple $(U , \, V) \in (\mathbb{K}[\textrm{X}])^2$ tel que $A \, U + B \, V = 1$ , avec $\textrm {deg} \, U< n$ et $\textrm {deg} \, V < n$ .

Vrai ou Faux ?

Correction :

$\bullet$ Existence
On sait qu’il existe $(U , \, V) \in (\mathbb{K}[\textrm{X}])^2$ tel que $A \, U + B \, V = 1$ ,
Par division euclidienne
$U = B \, Q_0 + U_0$ et $V = A \, Q_1 + V_0$ avec
$\textrm {deg} \, U_0 < \textrm {deg} \, B$ et $\textrm {deg} \, V_0 < \textrm {deg} \, B$
donc $\textrm {deg} \,U_0 < n$ et $\textrm {deg} \,V_0 < n$

Alors $A \, U + B \, V = A \wedge B$ donne
$A \, U_0 + B \, V_0 + A\,B\, (Q_0 + Q_1) = 1$
donc
$A\,B\, (Q_0 + Q_1) = 1 - A \, U_0 -B \, V_0$

Comme $\textrm {deg} (A \, U_0 ) \leq \textrm {deg}\,( A) + \textrm {deg}\,( U_0 )$
$\textrm {deg}( A \, U_0) < \textrm {deg}\, (A) + \textrm {deg}\, (B)$
$\textrm {deg}( A \, U_0) < \textrm {deg}\, (A \, B)$ .
De même $\textrm {deg}( B \, V_0) < \textrm {deg}\, (A \, B)$
donc $\textrm {deg}( B \, V_0) < \textrm {deg}\, (A \, B)$
donc $\textrm {deg}( 1 - A \, U_0 -B \, V_0 ) < \textrm {deg}\, (A \, B)$ .

La relation $A\,B\, (Q_0 + Q_1) = 1 - A \, U_0 -B \, V_0$
implique que $\textrm {deg}(A\,B\, (Q_0 + Q_1)) < \textrm {deg}\, (A \, B)$
donc $A\,B\, (Q_0 + Q_1) = 0 \Rightarrow Q_0 + Q_1 = 0$
et on a obtenu $A \, U_0 + B \, V_0 = 1$
avec $\textrm {deg}\, U_0 < n$ et $\textrm {deg}\, V_0 < n$ .

$\bullet$ Unicité
On suppose que
$A \, U_0 + B \, V_0 = 1$ et $A \, U_1 + B \, V_1 = 1$
avec $U_0\, , U_1 \, V_0 \, , V_1$ de degré strictement inférieur à $n$ .
donc $A (U_0 - U_1) = B(V_1 - V_0)$ .
Comme $A \wedge B = 1$ , $A$ divise $B(V_1 - V_0)$ donne par le théorème de Gauss
$A$ divise $V_1 - V_0$ avec $\textrm{deg} (V_1 - V_0) < \textrm{deg} A$ ,
donc $V_1 - V_0 = 0$ et alors $U_0 - U_1 = 0$ .
On a prouvé l’unicité du couple.

L’intégralité des chapitres au programme de Maths en Maths Sup sont accessibles en cours en ligne gratuitement. Les étudiants de MPSI, PCSI et PTSI pourront ainsi prendre de l’avance sur le programme en commençant leurs révisions sur les chapitres qui arrivent :

Exercices corrigés sur l’Arithmétique et Polynômes en Maths Sup

Plan des exercices d’Arithmétique et Polynômes

COURS DE MATHS

Les meilleurs professeurs particuliers

Pour progresser et réussir

1. Calculs de PGCD en cours d’arithmétique maths sup

Exercice 1 :

2. une suite de polynômes

3. Exercice 3

4. Reste d’une division euclidienne

5. Détermination d’un pgcd

COURS PARTICULIERS EN LIGNE

Nous avons sélectionné pour vous les meilleurs professeurs particuliers.

POUR ACCÉLÉRER MA PROGRESSION

6. Théorème de Bezout précisé

Contact

Qui sommes-nous ?

Nous rejoindre

Copyright @ GROUPE REUSSITE - Mentions légales