Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les dérivées en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices de dérivées
1. Autour de la formule de Leibniz
2. Généralisation du théorème de Rolle pour un intervalle qui n’est pas un segment
3. Utilisation du théorème de Rolle
4. Autour du théorème des accroissements finis.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Application de la formule de Leibniz
Exercice 1.
Soit ![]() . Dérivée
. Dérivée ![]() -ième de
-ième de ![]() .
.
Correction :
![]() On se place sur
On se place sur ![]() .
.
On note ![]() et
et ![]()
![]() et si
et si ![]() ,
, ![]() .
.
Par la formule de Leibniz
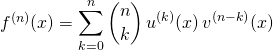
avec ![]() si
si ![]() .
.
Donc si ![]() ,
,
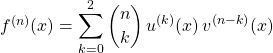
![]()
![]() .
.
⚠️ ![]() et
et ![]() si
si ![]() ne s’expriment pas de la même façon !
ne s’expriment pas de la même façon !
Ce qui conduit à distinguer les cas ![]() et
et ![]() .
.
![]() Si
Si ![]() ,
,
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]() , donc
, donc
![]()
![]()
![]()
![]()
avec ![]()
![]()
Après calculs,
![]()
![]()
![]()
Exercice 2
Soit ![]() . Calculer la dérivée
. Calculer la dérivée ![]() -ième de
-ième de ![]() .
.
Correction :
On se place sur ![]() .
.
On note ![]() et
et ![]()
![]()
si ![]() ,
, ![]()
si ![]()
![]()
et ![]() .
.
Par la formule de Leibniz
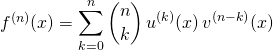
Il suffit donc de sommer de ![]() à
à ![]() et dans ce cas
et dans ce cas ![]()
![]()

![]()
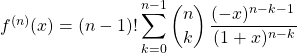
![]() Le seul terme de la somme non nul en
Le seul terme de la somme non nul en ![]() est celui pour
est celui pour ![]() :
:
![]()
![]() Si
Si ![]() ,
, 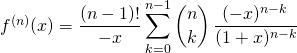
par le binôme de Newton (en faisant attention qu’il manque le terme pour ![]() qui est égal à 1)
qui est égal à 1)
![]()
![]() .
.
Exercice 3
En dérivant ![]() fois
fois ![]() , on obtient
, on obtient 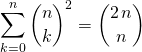 . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
![]() Soit
Soit ![]() et
et ![]() .
.
Si ![]() ,
, ![]()
et ![]() .
.
Par la formule de Leibniz :
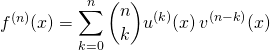
![]()
![]()
![]()
donc

![]() est une fonction polynôme de degré
est une fonction polynôme de degré ![]() de coefficient dominant
de coefficient dominant  .
.
![]() On écrit
On écrit ![]() avec
avec ![]()
donc ![]()
Le coefficient de ![]() dans cette écriture est
dans cette écriture est ![]() .
.
![]() En égalant les deux valeurs de
En égalant les deux valeurs de ![]() , on obtient
, on obtient
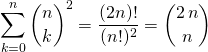 .
.
Exercice 4
Soient ![]() et
et ![]() .
.
En dérivant ![]() fois la fonction
fois la fonction ![]() ,
,
on obtient :
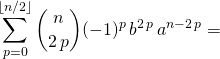
![]() . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
La relation n’est pas vraie si ![]() est impair,
est impair, ![]() et
et ![]() .
.
![]() Soit
Soit ![]() .
.
Alors ![]()
On note ![]() et
et ![]() un argument de
un argument de ![]()
![]() et
et ![]() est du signe de
est du signe de ![]()
donc ![]()
![]()
![]() .
.
En écrivant ![]() , on obtient
, on obtient ![]()
![]() On note
On note ![]() et
et ![]()
Si ![]() ,
, ![]()
et ![]() .
.
Par la formule de Leibniz,
![]()
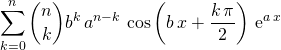
![]() En prenant la valeur en
En prenant la valeur en ![]() ,
,
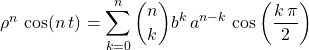
si ![]() ,
, ![]()
si ![]() ,
, ![]()
![]()
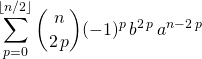
![]() si
si ![]() ,
,
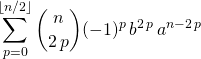
![]()
![]() si
si ![]() , on utilise
, on utilise ![]()
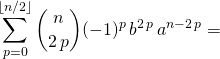
![]()
Exercice 5
Soit ![]() .
. ![]() .
.
Montrer que ![]() .
.
Correction :
Si ![]() , on note
, on note ![]() .
.
Si ![]() , on note
, on note ![]() .
.
![]() Pour
Pour ![]() ,
,
![]()
![]() est vérifiée.
est vérifiée.
![]() On suppose que
On suppose que ![]() est vraie.
est vraie.
On écrit si ![]() ,
, ![]() avec
avec ![]() .
.
Par la formule de Leibniz,
![]()
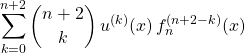
Pour tout ![]() .
.
Comme ![]() , il suffit donc de sommer de
, il suffit donc de sommer de ![]() à
à ![]() , alors
, alors
![]()
![]()
![]()
![]()
En dérivant la relation donnée par ![]() :
:
![]()
![]()
![]()
![]()
![]() où
où
![]()
![]()
![]()
et donc ![]() .
.
La propriété est démontrée par récurrence.
2. Théorème de Rolle
Exercice 1
Soit ![]() une fonction réelle continue sur
une fonction réelle continue sur ![]() , dérivable sur
, dérivable sur ![]() qui admet
qui admet ![]() pour limite en
pour limite en ![]() .
.
Montrer qu’il existe ![]() que
que ![]() .
.
Correction :
![]() Si
Si ![]() décrit
décrit ![]() ,
, ![]() décrit
décrit ![]() . On choisit
. On choisit ![]() .
.
![]() définit une bijection de
définit une bijection de ![]() sur
sur ![]() .
.
On note ![]() où pour tout
où pour tout ![]() de
de ![]()
![]() .
.
![]()
![]() est continue sur
est continue sur ![]() à valeurs dans
à valeurs dans ![]() .
.
![]()
![]() .
.
On prolonge ![]() par continuité en
par continuité en ![]() en posant
en posant ![]() .
.
![]()
![]() .
.
![]()
![]() est dérivable sur
est dérivable sur ![]() .
.
Par application du théorème de Rolle, il existe ![]() tel que
tel que ![]()
soit ![]() .
.
En notant ![]() ,
, ![]() ce qui est le résultat attendu.
ce qui est le résultat attendu.
Exercice 2
Question 1
Soit ![]() une fonction dérivable sur
une fonction dérivable sur ![]() admettant une même limite finie
admettant une même limite finie ![]() en
en ![]() et
et ![]() .
.
Montrer qu’il existe ![]() tel que
tel que ![]()
Correction :
On note pour tout ![]() de
de ![]() ,
, ![]() .
.
On prolonge ![]() par continuité en posant
par continuité en posant ![]() .
.
![]()
![]() est continue sur
est continue sur ![]()
![]()
![]() est dérivable sur
est dérivable sur ![]()
![]()
![]() .
.
Par le théorème de Rolle, il existe ![]() tel que
tel que ![]() .
.
soit ![]() donc
donc ![]() .
.
Alors si ![]() , ce qui donne le résultat attendu.
, ce qui donne le résultat attendu.
Question 2
Soit ![]() une fonction réelle dérivable sur
une fonction réelle dérivable sur ![]() et admettant
et admettant ![]() pour limite en
pour limite en ![]()
Montrer qu’il existe ![]() tel que
tel que ![]() .
.
Correction :
![]() est continue sur
est continue sur ![]() et admet la même limite
et admet la même limite ![]() en
en ![]() .
.
D’après la question 1, il existe ![]() tel que
tel que ![]() .
.
Or ![]() ssi
ssi ![]() ce qui donne le résultat attendu.
ce qui donne le résultat attendu.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. Utilisation du théorème de Rolle
Exercice 1
Question 1
Soit ![]() une fonction dérivable sur l’intervalle
une fonction dérivable sur l’intervalle ![]() à valeurs dans
à valeurs dans ![]() qui s’annule
qui s’annule ![]() fois dans
fois dans ![]() avec
avec ![]() .
.
Pour tout réel ![]() ,
, ![]() s’annule au moins
s’annule au moins ![]() fois dans
fois dans ![]() .
.
Correction :
![]() est dérivable sur
est dérivable sur ![]() à valeurs réelles.
à valeurs réelles.
On note ![]() les
les ![]() zéros de
zéros de ![]() rangés par ordre strictement croissant.
rangés par ordre strictement croissant.
Soit ![]() ,
, ![]() est dérivable sur
est dérivable sur ![]() et
et ![]() .
.
Par application du théorème de Rolle, il existe ![]() tel que
tel que ![]() .
.
En utilisant ![]()
![]() ssi
ssi ![]() .
.
Les racines ![]() sont dans des intervalles deux à deux disjoints, donc on a trouvé
sont dans des intervalles deux à deux disjoints, donc on a trouvé ![]() zéros distincts pour
zéros distincts pour ![]() .
.
Question 2.
Si ![]() est un polynôme de degré
est un polynôme de degré ![]() scindé à racines simples sur
scindé à racines simples sur ![]() , pour tout
, pour tout ![]() est scindé à racines simples (c’est-à-dire admet
est scindé à racines simples (c’est-à-dire admet ![]() racines réelles distinctes). Vrai ou faux ?
racines réelles distinctes). Vrai ou faux ?
Correction :
Le résultat est évident si ![]() .
.
Si ![]() , on note
, on note ![]() ,
, ![]() .
.
![]() est la somme d’un polynôme de degré
est la somme d’un polynôme de degré ![]() et d’un polynôme de degré
et d’un polynôme de degré ![]() , c’est un polynôme de degré
, c’est un polynôme de degré ![]() .
.
Par la première question, ![]() admet
admet ![]() racines distinctes notées
racines distinctes notées ![]() que l’on suppose rangées par ordre strictement croissant.
que l’on suppose rangées par ordre strictement croissant.
On note toujours ![]() .
.
![]() On suppose que
On suppose que ![]() .
.
Si ![]() ne s’annule pas sur l’intervalle
ne s’annule pas sur l’intervalle ![]() , la fonction continue
, la fonction continue ![]() garde un signe constant sur
garde un signe constant sur ![]() , donc
, donc ![]() est monotone sur
est monotone sur ![]() .
.
On rappelle que ![]() et que
et que ![]() .
.
Par croissance comparée, ![]() .
.
Par la monotonie de ![]() sur
sur ![]() ,
, ![]() est nulle sur cet intervalle, il en est de même de
est nulle sur cet intervalle, il en est de même de ![]() , ce qui est absurde.
, ce qui est absurde.
Donc ![]() s’annule sur
s’annule sur ![]() en
en ![]() et
et ![]() admet
admet ![]() racines distinctes.
racines distinctes.
![]() On suppose que
On suppose que ![]() .
.
Si ![]() ne s’annule pas sur
ne s’annule pas sur ![]() ,
, ![]() garde un signe constant sur
garde un signe constant sur ![]() , donc
, donc ![]() est monotone sur
est monotone sur ![]() .
.
On rappelle que ![]() et que
et que ![]() .
.
Par croissance comparée, ![]() .
.
Par la monotonie de ![]() sur
sur ![]() ,
, ![]() est nulle sur cet intervalle, il en est de même de
est nulle sur cet intervalle, il en est de même de ![]() , ce qui est absurde.
, ce qui est absurde.
Donc ![]() s’annule sur
s’annule sur ![]() en
en ![]() et
et ![]() admet
admet ![]() racines distinctes.
racines distinctes.
Dans les deux cas, on a prouvé que ![]() est scindé à racines simples.
est scindé à racines simples.
En divisant par ![]() , on a prouvé que
, on a prouvé que ![]() est scindé à racines simples.
est scindé à racines simples.
Exercice 2
Soit ![]() une fonction deux fois dérivable sur
une fonction deux fois dérivable sur ![]() (
(![]() ) à valeurs réelles et telle que
) à valeurs réelles et telle que ![]() et
et ![]() où
où ![]() sur
sur ![]() .
.
Montrer que ![]() est nulle sur
est nulle sur ![]() .
.
Correction :
![]()
![]() est deux fois dérivable sur
est deux fois dérivable sur ![]()
![]()
![]()
donc ![]() est croissante sur
est croissante sur ![]() .
.
![]() Comme
Comme ![]() , le théorème de Rolle donne l’existence de
, le théorème de Rolle donne l’existence de ![]() tel que
tel que ![]() .
.
La croissance de ![]() donne
donne ![]() si
si ![]() et
et ![]() si
si ![]() .
.
![]()
![]() est décroissante sur
est décroissante sur ![]() et croissante sur
et croissante sur ![]() .
.
Donc ![]() car
car ![]() .
.
Comme ![]() est à valeurs positives ou nulles, on a prouvé que
est à valeurs positives ou nulles, on a prouvé que ![]() soit
soit ![]() .
.
Exercice 3
Soit ![]() une fonction dérivable sur un intervalle
une fonction dérivable sur un intervalle ![]() à valeurs dans
à valeurs dans ![]() et soit
et soit ![]() son graphe. Soient
son graphe. Soient ![]() et
et ![]() deux points de
deux points de ![]() distincts tels que
distincts tels que ![]() soit sur la tangente en
soit sur la tangente en ![]() à
à ![]() . Montrer qu’il existe un point
. Montrer qu’il existe un point ![]() de
de ![]() tel que
tel que ![]() soit sur la tangente en
soit sur la tangente en ![]() à
à ![]() .
.
Correction :
![]() Analyse du problème :
Analyse du problème :
Si ![]() , la tangente en
, la tangente en ![]() à
à ![]() a pour équation
a pour équation
![]() .
.
On cherche donc ![]() tel que
tel que ![]()
soit ![]() .
.
![]() Résolution :
Résolution :
Une équation de la tangente en ![]() à
à ![]() étant
étant ![]() , on sait qu’il existe
, on sait qu’il existe ![]() ,
, ![]() tel que
tel que ![]() .
.
On définit la fonction ![]() sur
sur ![]() (si
(si ![]() ) et sur
) et sur ![]() si
si ![]() ) par
) par ![]() et
et ![]() .
.
![]() est continue sur
est continue sur ![]() car
car ![]() est dérivable sur
est dérivable sur ![]() et continue en
et continue en ![]() , par définition de
, par définition de ![]() .
.
![]() est dérivable sur
est dérivable sur ![]() (ou sur
(ou sur ![]() )
)
et ![]() .
.
Par le théorème de Rolle, il existe ![]() (ou
(ou ![]() ) tel que
) tel que ![]() .
.
or ![]() ,
,
![]() , donc la tangente au point
, donc la tangente au point ![]() à la courbe
à la courbe ![]() passe par
passe par ![]() .
.
Exercice 4
Formule de Taylor Lagrange
Soit ![]() un intervalle et
un intervalle et ![]() et
et ![]() deux éléments distincts de
deux éléments distincts de ![]() .
.
Soit ![]() une fonction réelle de classe
une fonction réelle de classe ![]() sur
sur ![]() et
et ![]() fois dérivable sur
fois dérivable sur ![]() .
.
Si ![]() et
et ![]() sont deux éléments distincts de
sont deux éléments distincts de ![]() , il existe
, il existe ![]() strictement compris entre
strictement compris entre ![]() et
et ![]() tel que
tel que
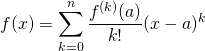
![]() .
.
indication :
appliquer le théorème de Rolle à la fonction 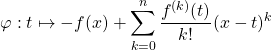
![]()
pour ![]() convenablement choisi.
convenablement choisi.
Correction :
On note ![]() (ou
(ou ![]() )
)
et ![]() (ou
(ou ![]() ).
).
![]() On remarque que
On remarque que ![]() .
.
On choisit ![]() tel que
tel que ![]() (ce qui donne une équation du premier degré en
(ce qui donne une équation du premier degré en ![]() ).
).
![]()
![]() est continue sur
est continue sur ![]() à valeurs dans
à valeurs dans ![]()
![]()
![]() est dérivable sur
est dérivable sur ![]() .
.
Par le théorème de Rolle, il existe ![]() strictement compris entre
strictement compris entre ![]() et
et ![]() tel que
tel que ![]() .
.

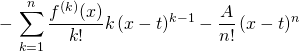
en posant ![]() dans la deuxième somme :
dans la deuxième somme :
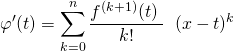
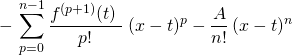
par télescopage
![]()
en traduisant ![]() avec
avec ![]() , on obtient
, on obtient ![]() .
.
Puis ![]() donne
donne
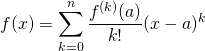
![]()
4. Accroissements finis
Exercice 1
Question 1
Soient ![]() et
et ![]() deux fonctions continues sur
deux fonctions continues sur ![]() à valeurs dans
à valeurs dans ![]() , dérivables sur
, dérivables sur ![]() et telles que
et telles que ![]() .
.
Montrer qu’il existe ![]() dans
dans ![]() tel que
tel que ![]() .
.
Correction :
⚠️ si l’on applique deux fois le théorème des accroissements finis (à ![]() et à
et à ![]() ), on écrit
), on écrit ![]() et
et ![]() .
.
Les réels ![]() et
et ![]() ne sont pas égaux et on n’a pas prouvé le résultat.
ne sont pas égaux et on n’a pas prouvé le résultat.
![]() est continue sur
est continue sur ![]() , dérivable sur
, dérivable sur ![]() à valeurs réelles,
à valeurs réelles,
![]()
ssi ![]()
Si l’on avait ![]() , il existerait
, il existerait ![]() tel que
tel que ![]() , ce qui est exclu.
, ce qui est exclu.
![]() , donc
, donc ![]() .
.
Par application du théorème de Rolle à ![]() , il existe
, il existe ![]() tel que
tel que ![]() soit
soit ![]() avec
avec ![]() .
.
En égalant les deux valeurs de ![]() obtenues, on a prouvé que
obtenues, on a prouvé que
![]() .
.
Question 2
Soit ![]() une fonction de classe
une fonction de classe ![]() sur
sur ![]() à valeurs dans
à valeurs dans ![]() , trois fois dérivable sur
, trois fois dérivable sur ![]() .
.
Montrer qu’il existe ![]() de
de ![]() tel que
tel que ![]()
![]() .
.
Correction :
On note
![]()
![]()
et ![]() .
.
![]() et
et ![]() sont deux fois dérivables sur
sont deux fois dérivables sur ![]() et
et ![]() ne s’annule pas sur
ne s’annule pas sur ![]()
Il existe donc ![]() tel que
tel que ![]()
soit ![]() .
.
![]() et
et ![]() .
.
![]() et
et ![]() sont dérivables sur
sont dérivables sur ![]() et
et ![]() ne s’annule pas sur
ne s’annule pas sur ![]() .
.
On peut donc utiliser la question 1 sur ![]() .
.
Il existe ![]() tel que
tel que
![]()
soit
![]()
Par application du théorème des accroissements finis à ![]() qui est continue sur
qui est continue sur ![]() et dérivable sur
et dérivable sur ![]() , il existe
, il existe ![]() tel que
tel que
![]() donc
donc ![]() ,
,
ce qui est la relation demandée.
Exercice 2
Soit ![]() une fonction dérivable et bornée sur
une fonction dérivable et bornée sur ![]() .
.
On suppose que ![]() est monotone.
est monotone.
Montrer que ![]() est constante.
est constante.
Exercice 3
Question 1
Soit ![]() une fonction dérivable sur
une fonction dérivable sur ![]() à valeurs réelles telle que
à valeurs réelles telle que ![]() .
.
Montrer que ![]() .
.
Question 2
a) On note ![]()
Quelle est la limite en ![]() de
de ![]() ?
?
b) ![]() a une limite en
a une limite en ![]()
Exercice 4
Soit ![]() une fonction définie sur
une fonction définie sur ![]() à valeurs dans
à valeurs dans ![]() , continue sur
, continue sur ![]() et dérivable sur
et dérivable sur ![]() telle que
telle que ![]() soit strictement croissante sur
soit strictement croissante sur ![]() .
.
Question 1
a) Pour tout ![]() de
de ![]() , il existe un et un seul
, il existe un et un seul ![]() de
de ![]() tel que
tel que ![]() .
.
b) On définit pour tout ![]() de
de ![]() ,
, ![]() .
.
Montrer que ![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() et strictement croissante sur
et strictement croissante sur ![]() .
.
Question 2
On définit ![]() par
par ![]() et
et ![]() ,
, ![]()
où ![]() est l’unique point de
est l’unique point de ![]() tel que
tel que ![]() .
.
a) Montrer que ![]() est strictement croissante sur
est strictement croissante sur ![]() et
et ![]() .
.
b) Montrer que ![]() est continue.
est continue.
c) On suppose que ![]() est de classe
est de classe ![]() sur
sur ![]() et que
et que ![]() ne s’annule pas sur
ne s’annule pas sur ![]() . Montrer que
. Montrer que ![]() est de classe
est de classe ![]() sur
sur ![]() .
.
Le programme de Maths en Maths Sup, que ce soit en MPSI, PCSI ou PTSI, est très complexe. Prendre de l’avance en se familiarisant sur les chapitres à venir est un bon moyen de progresser durablement. Pour cela, vous pouvez d’ores et déjà jeter un œil aux chapitres suivants :

