Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur le calcul des déterminants MPSI, PCSI et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Exercices sur le calcul des déterminants en maths sup
1. Calculer le déterminants d’ordre inférieur ou égal à 4
Exercice 1 :
Sous forme factorisée, calculer le déterminant :
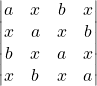
Exercice 2 :
Sous forme factorisée, calculer le déterminant :
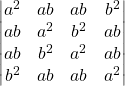
2. Calculer le déterminant de Vandermonde
Exercice : Calculer le déterminant de Vandermonde ![]() à l’aide de factorielles.
à l’aide de factorielles.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
3. Calculer le déterminants d’ordre 
Exercice :
Soient ![]() et
et ![]()
![]() réels deux à deux distincts.
réels deux à deux distincts.
On pose 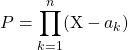
et si ![]() ,
, ![]() .
.
Calculer si ![]() ,
,
![]()
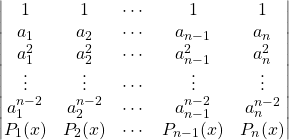
4. Calculer le déterminants d’endomorphismes
Calculer ![]() où
où ![]() .
.
5. Calculer le déterminant avec opérations
Exercice 1 :
Soit ![]() telle que
telle que ![]()
![]() et est divisible par
et est divisible par ![]() .
.
Exercice 2 :
Soient ![]() et
et ![]() de
de ![]() telles que
telles que ![]() . Démontrer que
. Démontrer que ![]() .
.
On commencera par le cas où ![]() .
.
6. Calculer le déterminants sur la comatrice
Exercice :
Soit ![]() et
et ![]() .
.
![]() .
.
Corrigés des exercices sur le calcul des déterminants :
1. Corrigé de l’exercice : Calculer le déterminants d’ordre inférieur ou égal à 4
Exercice 1 : La somme des termes de chaque ligne est constante.
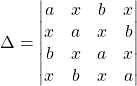
En utilisant l’opération ![]()
puis en factorisant ![]() :
:
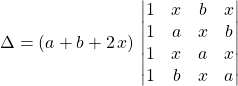
par ![]() si
si ![]()
![]()
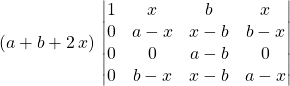
On développe suivant la première colonne :
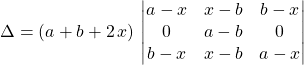
puis suivant la deuxième ligne :
![]()
![]()
![]()
![]() .
.
Exercice 2 :
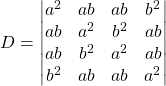
par ![]() et
et ![]() ,
, ![]() est égal à
est égal à
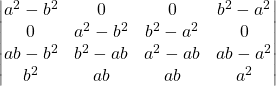
On factorise ![]() dans
dans![]() et
et ![]() , et
, et ![]() dans
dans ![]() ,
,
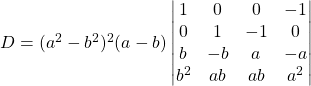
par ![]() et
et ![]() ,
,
![]() est égal à
est égal à
![]()
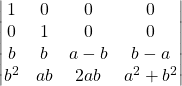
par les déterminants par blocs :
![]()
![]()
on factorise ![]() dans la ligne 1 :
dans la ligne 1 :
![]()
![]()
![]()
soit ![]() .
.
2. Corrigé de l’exercice : Calculer le déterminant de Vandermonde
![]()
![]() On fixe
On fixe ![]() et on calcule
et on calcule 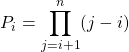 .
.
On pose ![]() ,
, 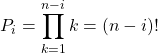
![]()
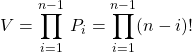
En posant ![]() ,
, 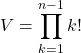 .
.
On peut aussi écrire que 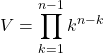 .
.
3. Corrigé de l’exercice : Calculer le déterminants d’ordre 
![]()
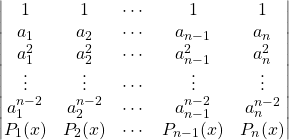
On développe le déterminant suivant la dernière ligne :
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
ce que l’on peut résumer sous la forme
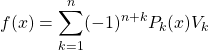 où
où ![]()
Si ![]() ,
, ![]() car
car ![]() est un polynôme unitaire dont les racines sont
est un polynôme unitaire dont les racines sont ![]() .
.
![]()
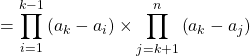
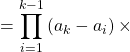
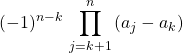
![]()
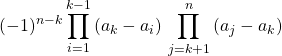
![]() avec
avec
![]()
![]()
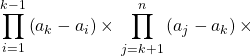
![]()
![]()
![]() .
.
![]() est une fonction polynôme de degré inférieur ou égal à
est une fonction polynôme de degré inférieur ou égal à ![]() , prenant en
, prenant en ![]() valeurs distinctes la valeur
valeurs distinctes la valeur ![]() ,
,
donc ![]() est une fonction constante et pour tout
est une fonction constante et pour tout ![]() ,
, ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
4. Corrigé de l’exercice : Calculer le déterminant d’endomorphisme
On sait que ![]() .
.
On note :
![]() et
et ![]() .
.
Soit ![]() une base adaptée à cette somme directe.
une base adaptée à cette somme directe.
On a ![]() et
et ![]() , la matrice de
, la matrice de ![]() est donc la matrice diagonale
est donc la matrice diagonale ![]() .
.
![]() avec
avec ![]() .
.
5. Corrigé de l’exercice : Calculer le déterminants avec opération
En utilisant la formule 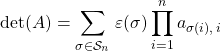 ,
,
![]() est une somme d’éléments de
est une somme d’éléments de ![]() , donc
, donc ![]() .
.
On note ![]() les vecteurs colonnes de
les vecteurs colonnes de ![]() et
et ![]() la base canonique de
la base canonique de ![]() ,
, ![]() .
.
On utilise les opérations : ![]() ,
,
![]()
où ![]()
les éléments de ![]() sont la somme de deux éléments de
sont la somme de deux éléments de ![]() , ils sont égaux à
, ils sont égaux à ![]() ou
ou ![]() .
.
On peut donc mettre en facteur ![]() dans les
dans les ![]() premières colonnes,
premières colonnes, ![]() et
et ![]()
![]() où
où ![]()
donc ![]() , ce qui prouve que
, ce qui prouve que ![]() divise
divise ![]() .
.
6. Corrigé de l’exercice : Calculer le déterminant sur la comatrice
![]() Si
Si ![]() ,
, ![]() .
.
![]() Si
Si ![]() ,
, ![]() n’est pas inversible (sinon en multipliant par son inverse, on aurait
n’est pas inversible (sinon en multipliant par son inverse, on aurait ![]() ), alors
), alors ![]() donc
donc ![]() , donc
, donc
![]() .
.
![]() Si
Si ![]() , tous les cofacteurs sont nuls et
, tous les cofacteurs sont nuls et ![]() , donc
, donc ![]() .
.
La relation est vérifiée lorsque ![]() n’est pas inversible.
n’est pas inversible.
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]() .
.
Vous pourrez retrouver beaucoup plus d’exercices dans l’application mobile PrepApp disponible sur les stores afin de vous exercer. N’hésitez pas à consulter d’aures chapitres :

