Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les équations différentielles en MPSI, MP2I, PCSI et PTSI
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Equations différentielles
- Équations différentielles d’ordre 1
- Équations différentielles d’ordre 2
- Systèmes différentiels
- Équations différentielles d’ordre 1
- Équations différentielles d’ordre 1 : problèmes de raccords
- Équations différentielles d’ordre 2 : changement de fonction inconnue
- Sur les graphes des solutions d’une équation différentielle
- Équations différentielles d’ordre 2 : problèmes de raccords
- Résolution d’une équation d’ordre 3 par changement de fonction inconnue
- Équations différentielles d’ordre 2 : solutions périodiques
- Équations différentielles d’ordre 2 : solutions de limite nulle en

On cherchera dans les exercices qui suivent l’ensemble des solutions réelles. Certains de ces exercices sont incontournables pour bien réussir en classe de MPSI, de PCSI, de PTSI ou encore de MP2I. Si vous ne parvenez à les résoudre ou à comprendre tous les corrigés contactez Groupe Réussite pour des cours particuliers de maths à domicile. Un enseignant à domicile vous aidera à comprendre ce chapitre très important pour la réussite de votre maths sup.
1. Exercices équations différentielles d’ordre 1 en maths sup
Exercice 1
Résoudre sur ![]() et sur
et sur ![]()
L’équation ![]() .
.
Exercice 2
![]()
Exercice 3
![]()
Exercice 4
Trouver ![]() dérivable sur
dérivable sur ![]() telle que
telle que ![]() et
et ![]() .
.
Exercice 5
Résoudre sur ![]() :
:
![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice 1 :
On peut remarquer que ![]() est la dérivée de
est la dérivée de ![]() et on sait qu’une primitive de
et on sait qu’une primitive de ![]() sur
sur ![]() est
est ![]() .
.
Il est alors plus simple de dire que ![]() est solution sur
est solution sur ![]()
ssi il existe ![]() tel que
tel que ![]() .
.
La solution générale sur ![]() est définie par
est définie par
![]() où
où ![]()
Correction de l’exercice 2 :
![]() où
où ![]() est la solution générale de l’équation sans second membre.
est la solution générale de l’équation sans second membre.
On cherche une solution de l’équation complète sous la forme ![]()
![]() est solution ssi
est solution ssi ![]()
ssi ![]()
On cherche ![]() sous la forme
sous la forme ![]()
![]()
![]() est solution
est solution
ssi ![]()
![]()
ssi 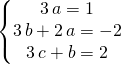
ssi ![]() .
.
On en déduit que
![]() est une solution particulière.
est une solution particulière.
L’ensemble des solutions est l’ensemble des fonctions
![]() où
où ![]() .
.
Correction de l’exercice 3 :
La solution générale de l’équation homogène est ![]() où
où ![]() .
.
En vue d’utiliser le principe de superposition des solutions, on écrit
![]()
![]() .
.
On cherche une solution de
![]()
sous la forme ![]() .
.
![]() est solution ssi
est solution ssi ![]()
![]() .
.
On cherche ![]() sous la forme
sous la forme ![]() .
.
0n obtient ![]()
ce qui donne ![]() et
et ![]() ssi
ssi ![]() et
et ![]()
donc ![]() est une solution particulière.
est une solution particulière.
On cherche une solution de
![]()
sous la forme ![]() .
.
![]() est solution ssi
est solution ssi ![]()
![]()
On cherche ![]() sous la forme
sous la forme ![]() ,
,
on obtient ![]()
ce qi donne ![]() et
et ![]() ssi
ssi ![]() et
et ![]()
donc ![]() est une solution particulière.
est une solution particulière.
![]() Par le principe de superposition des solutions
Par le principe de superposition des solutions ![]() est solution particulière
est solution particulière
![]()
L’ensemble des solutions est l’ensemble des fonctions :
![]()
![]() où
où ![]() .
.
Correction de l’exercice 4 :
![]() est solution d’une équation différentielle de la forme
est solution d’une équation différentielle de la forme ![]() .
.
La solution générale de ![]() est
est ![]() où
où ![]() .
.
![]() est solution particulière évidente.
est solution particulière évidente.
On en déduit que ![]()
avec ![]() soit
soit ![]() soit
soit ![]() .
.
On impose ![]()
Puis on traduit
![]()
ssi ![]()
![]()
ssi ![]() .
.
Sachant que ![]() , on obtient
, on obtient ![]() soit
soit ![]()
et donc ![]() .
.
La solution du problème est définie par ![]() .
.
Correction de l’exercice 5 :
On écrit l’équation sous la forme ![]() .
.
Une primitive de ![]() est
est ![]()
donc la solution générale sur ![]() est
est ![]() soit
soit ![]() où
où ![]()
On utilise la méthode de variation de la constante ![]() est solution sur
est solution sur ![]() ssi
ssi
ssi ![]()
ssi ![]()
ssi ![]()
La solution générale est définie par ![]() où
où ![]() .
.
2. Exercices corrigés équations différentielles d’ordre 2 en maths sup
Exercice 1
![]() avec
avec ![]() et
et ![]() .
.
Exercice 2
![]()
avec ![]() et
et ![]() .
.
Exercice 3
Résoudre ![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice 1 :
![]()
![]()
La solution générale de l’équation homogène est ![]() où
où ![]() .
.
On cherche une solution particulière de
![]() sous la forme
sous la forme ![]() car
car ![]() est racine simple de
est racine simple de ![]() .
.
![]()
et ![]() .
.
![]() est solution ssi
est solution ssi ![]() ssi
ssi ![]()
donc ![]() .
.
On cherche une solution particulière de ![]() sous la forme
sous la forme ![]()
![]() est solution ssi
est solution ssi ![]()
ssi ![]() et
et ![]() ssi
ssi ![]() et
et ![]()
soit ![]() .
.
La solution générale de l’équation est donnée par le principe de superposition des solutions par
![]()
où ![]() .
.
![]() On détermine la fonction
On détermine la fonction ![]() vérifiant les conditions initiales.
vérifiant les conditions initiales.
![]() ssi
ssi ![]()
et comme ![]()
![]() .
.
On résout donc le système :
![]() ssi
ssi ![]() et
et ![]() .
.
La fonction ![]() cherchée est définie par
cherchée est définie par
![]()
Correction de l’exercices 2 :
L’équation caractéristique ![]()
admet deux racines distinctes ![]() et
et ![]() .
.
La solution générale de l’équation homogène est ![]() où
où ![]() .
.
On cherche une solution particulière de ![]() de la forme
de la forme ![]() où
où ![]() .
.
![]()
![]()
![]() .
.
![]() est solution ssi
est solution ssi ![]()
ssi ![]() ssi
ssi ![]()
![]()
Puis ![]() est solution particulière de
est solution particulière de ![]()
soit : ![]() .
.
On en déduit que la solution générale est définie par ![]()
Traduction des conditions initiales
![]() et
et ![]()
ssi ![]() et
et ![]()
ssi ![]() et
et ![]()
La fonction cherchée est définie par
![]()
Correction de l’exercice 3 :
L’équation caractéristique
![]()
admet deux racines ![]() et
et ![]() .
.
La solution générale de l’equation homogène est
![]()
où ![]()
On cherche une solution particulière
![]() de
de ![]() sous la forme
sous la forme ![]() où
où ![]() .
.
![]()
![]() .
.
![]() est solution
est solution
ssi ![]()
ssi ![]() ssi
ssi ![]() .
.
Puis ![]() est solution particulière de
est solution particulière de ![]()
ce qui donne ![]()
On cherche une solution particulière ![]() de
de ![]() sous la forme
sous la forme ![]() où
où ![]() .
.
![]()
![]()
![]()
![]() est solution ssi pour tout réel
est solution ssi pour tout réel ![]() ,
,
![]()
ssi ![]() ssi
ssi ![]()
soit ![]()
Et ![]() est solution particulière de
est solution particulière de ![]()
![]() .
.
La solution générale est définie par ![]()
![]()
où ![]() .
.
3. Systèmes différentiels : exercices en MPSI, MP2I, PTSI et PCSI
Exercice 1
Déterminer l’ensemble des fonctions ![]() et
et ![]() de la variable
de la variable ![]() vérifiant sur
vérifiant sur ![]()
![]()
Correction : ![]() En utilisant
En utilisant ![]() ,
,
on peut conclure que par somme de 3 fonctions dérivables, ![]() est dérivable. Puis en dérivant :
est dérivable. Puis en dérivant :
![]() ,
, ![]() .
.
On utilise la seconde équation du système ![]()
pour obtenir :
![]() .
.
De la première équation, on tire ![]() en fonction de
en fonction de ![]() et
et ![]() :
:
![]()
ce qui donne pour tout réel ![]() ,
,
![]()
![]() .
.
soit ![]() .
.
![]() Résolution de l’équation différentielle
Résolution de l’équation différentielle
![]() L’équation
L’équation ![]() a pour solution générale
a pour solution générale ![]() où
où ![]() .
.
![]() Il est évident que
Il est évident que ![]() est solution particulière de
est solution particulière de ![]()
![]()
![]() est solution particulière de
est solution particulière de ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
On en déduit qu’il existe ![]() ,
,
![]() ,
, ![]() .
.
![]() En utilisant :
En utilisant : ![]() , on obtient après calculs, pour tout réel
, on obtient après calculs, pour tout réel ![]() ,
,
![]()
![]() .
.
![]() Il reste à étudier la réciproque.
Il reste à étudier la réciproque.
La première équation est vérifiée, car c’est elle qui a servi à déterminer ![]() .
.
Il reste à vérifier la deuxième.
On calcule si ![]()
![]() en utilisant
en utilisant ![]() , donc
, donc ![]() ,
,
![]()
![]()
![]() en utilisant l’équation différentielle dont
en utilisant l’équation différentielle dont ![]() est solution, on a donc obtenu
est solution, on a donc obtenu
![]()
la deuxième équation est vérifiée.
La réciproque est vraie.
Conclusion : les solutions du système sont définies pour tout réel ![]() par :
par :
![]()
et ![]()
![]()
où ![]() .
.
Exercice 2
Déterminer l’ensemble des fonctions ![]() et
et ![]() de la variable
de la variable ![]() vérifiant sur
vérifiant sur ![]()
![]()
Correction :
On sait qu’un système de deux équations ![]() est équivalent au système formé par
est équivalent au système formé par ![]() et
et ![]()
On obtient donc le système équivalent
![]()
![]() en posant
en posant ![]() , on résout
, on résout ![]() dont l’équation caractéristique
dont l’équation caractéristique ![]() admet comme solution générale
admet comme solution générale ![]() .
.
![]() En posant
En posant ![]() , on résout
, on résout ![]() ce qui donne
ce qui donne ![]() où
où ![]() .
.
![]() On termine en utilisant
On termine en utilisant
![]() et
et ![]() ,
,
ce qui donne pour tout ![]()
![]()
![]() .
.
où ![]() .
.
4. Équations différentielles d’ordre 1, solution périodique
Soit ![]() une fonction continue sur
une fonction continue sur ![]() et 1-périodique. Soit
et 1-périodique. Soit ![]() .
.
Il existe une unique solution de ![]() qui est 1-périodique. Vrai ou Faux ?
qui est 1-périodique. Vrai ou Faux ?
Correction : ![]() On résout d’abord l’équation.
On résout d’abord l’équation.
![]()
![]() est solution générale de l’équation sans second membre.
est solution générale de l’équation sans second membre.
![]() On utilise la méthode de variation de la constante
On utilise la méthode de variation de la constante ![]() est solution de l’équation
est solution de l’équation
ssi ![]()
ssi ![]()
ssi ![]()
![]() .
.
On en déduit que la solution générale de l’équation est donnée par
![]()
où ![]() .
.
![]() Recherche d’une solution 1-périodi- que :
Recherche d’une solution 1-périodi- que :
![]() est
est ![]() -périodique
-périodique
ssi ![]()
![]()
![]()
ssi ![]() ,
,
![]()
![]() (*)
(*)
On calcule par la relation de Chasles :
![]()
![]()
On utilise le changement de variable : ![]() dans la deuxième intégrale (
dans la deuxième intégrale (![]() ),
), ![]() est de classe
est de classe ![]() sur
sur ![]() :
:
![]()
ce qui donne puisque ![]() est
est ![]() -périodique
-périodique
![]()
La condition nécessaire et suffisante (*) s’écrit alors ![]() ,
,
![]()
![]()
ssi ![]()
ssi ![]()
ssi ![]() .
.
Conclusion : il existe une et une seule solution ![]() – périodique.
– périodique.
5. Équations différentielles d’ordre 1 : problèmes de raccords
Exercice 1
![]() à résoudre sur
à résoudre sur ![]() ou
ou ![]() .
.
Puis déterminer les solutions sur ![]() .
.
Correction : ![]() Première partie
Première partie
0n résout l’équation sur ![]() ou
ou ![]() après l’avoir écrite sous la forme
après l’avoir écrite sous la forme ![]() .
.
![]() La solution générale de
La solution générale de ![]() est
est ![]() soit
soit ![]()
![]() On utilise la méthode de variation de la constante avec
On utilise la méthode de variation de la constante avec ![]() où
où ![]() sur
sur ![]() et
et ![]() sur
sur ![]() .
.
![]() est solution sur
est solution sur ![]()
ssi ![]()
ssi ![]()
On utilise ![]() de primitive
de primitive ![]() si
si ![]()
et ![]() de primitive
de primitive ![]() si
si ![]() .
.
![]() est solution sur
est solution sur ![]()
ssi ![]()
![]()
Donc la solution générale sur ![]() est
est
![]() où
où ![]()
et sur ![]() :
: ![]() où
où ![]() .
.
![]() Deuxième partie
Deuxième partie
Recherche d’une solution sur ![]() de
de ![]() .
.
On note ![]() si
si ![]()
et ![]() si
si ![]() .
.
![]() Si
Si ![]() ou
ou ![]() ,
, ![]() n’a pas de limite finie en
n’a pas de limite finie en ![]() .
.
![]() Si
Si ![]() , les limites de
, les limites de ![]() à gauche et à droite de
à gauche et à droite de ![]() sont nulles.
sont nulles.
On pose ![]() .
.
Dans ce cas, pour tout ![]() ,
, ![]() .
.
![]() est alors dérivable en
est alors dérivable en ![]() et
et ![]() .
.
On vérifie que ![]() , donc
, donc ![]() est encore solution de
est encore solution de ![]() en
en ![]() .
.
Elle est solution sur ![]() .
.
Conclusion : L’équation admet une unique solution sur ![]() définie par
définie par ![]() .
.
Exercice 2
Résoudre l’équation différentielle ![]()
sur ![]() et sur
et sur ![]() .
.
Déterminer les solutions sur ![]() .
.
Correction : ![]() Résolution sur
Résolution sur ![]() et sur
et sur ![]() .
.
On écrit l’équation sous la forme ![]() et on résout l’équation sur
et on résout l’équation sur ![]() avec
avec ![]() .
.
![]() La solution générale sur
La solution générale sur ![]() de
de ![]() est
est ![]() où
où ![]() car
car ![]() admet comme primitive
admet comme primitive ![]() .
.
![]() On utilise la méthode de variation de la constante.
On utilise la méthode de variation de la constante.
![]() est solution de
est solution de ![]() sur
sur ![]()
ssi ![]()
ssi ![]()
ssi ![]()
![]() .
.
L’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() où
où ![]() .
.
L’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions ![]() où
où ![]()
![]() Recherche de solutions de
Recherche de solutions de ![]() sur
sur ![]() .
.
On note ![]()
![]() Pour tout
Pour tout ![]() et
et ![]() ,
, ![]() admet
admet ![]() pour limite en
pour limite en ![]() . On pose
. On pose ![]() .
.
On introduit le taux d’accroissement de ![]() en
en ![]() :
:
![]()
alors ![]() .
.
![]() est dérivable en
est dérivable en ![]() et
et ![]() .
.
![]() est encore solution de l’équation en
est encore solution de l’équation en ![]() car
car ![]()
L’équation ![]() admet une infinité de solutions sur
admet une infinité de solutions sur ![]() .
.
Leurs graphes passent tous par l’origine.
⚠️ On peut remarquer que le théorème de Cauchy-Lipschitz ne s’applique pas sur ![]() car le coefficient de
car le coefficient de ![]() s’annule.
s’annule.
6. Équations différentielles d’ordre 2 : changement de fonction inconnue
Pour chaque question, on cherchera le domaine de dérivabilité et la dérivée.
Exercice 1
Résoudre sur ![]() l’équation
l’équation ![]() en posant
en posant ![]()
Correction : 👍 Il est important de ne pas oublier de démontrer que ![]() est deux fois dérivable.
est deux fois dérivable.
👍 On dérive ![]() en fonction de
en fonction de ![]() et non
et non ![]() en fonction de
en fonction de ![]() pour remplacer dans l’équation différentielle.
pour remplacer dans l’équation différentielle.
![]() Si
Si ![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() par produit de deux fonction 2 fois dérivable sur
par produit de deux fonction 2 fois dérivable sur ![]() ,
, ![]() l’est aussi.
l’est aussi.
![]() On écrit
On écrit ![]() ce qui permet de dériver plus facilement
ce qui permet de dériver plus facilement ![]() en fonction de
en fonction de ![]() .
.
Pour tout ![]() ,
,
![]()
![]()
![]()
![]()
👍 On remplace dans l’équation, en regroupant directement les termes en ![]() , ceux en
, ceux en ![]() et le seul terme en
et le seul terme en ![]() .
.
![]() est solution sur
est solution sur ![]() ssi
ssi ![]() ,
,
![]()
![]()
![]()
ssi ![]()
ssi ![]()
ssi ![]()
![]() .
.
⚠️ à ne pas oublier de donner les solutions ![]() .
.
L’ensemble des solutions sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions
![]() où
où ![]() .
.
Exercice 2
Résoudre l’équation ![]() sur
sur ![]() en posant
en posant ![]()
Correction : 👍 Il est important de ne pas oublier de démontrer que ![]() est deux fois dérivable.
est deux fois dérivable.
👍 On dérive ![]() en fonction de
en fonction de ![]() et non
et non ![]() en fonction de
en fonction de ![]() pour remplacer dans l’équation différentielle.
pour remplacer dans l’équation différentielle.
Si ![]() est deux fois dérivable sur
est deux fois dérivable sur ![]() ,
, ![]() l’est aussi.
l’est aussi.
![]() Recherche de la nouvelle équation différentielle
Recherche de la nouvelle équation différentielle
Si ![]() ,
,
![]()
![]()
![]() .
.
On remplace dans l’équation différentielle en regroupant dès le début les termes en ![]() et
et ![]() :
:
![]() est solution sur
est solution sur ![]() ssi pour tout
ssi pour tout ![]()
![]()
![]()
ssi ![]() .
.
![]() Détermination de
Détermination de ![]()
![]() La solution générale de
La solution générale de ![]() est
est ![]() où
où ![]() .
.
![]() La fonction
La fonction ![]() est solution particulière de
est solution particulière de ![]()
![]() La solution générale de
La solution générale de ![]() est
est
![]() où
où ![]()
![]() ⚠️ à donner les solutions
⚠️ à donner les solutions ![]() .
.
L’ensemble des solutions de ![]() sur
sur ![]() est l’ensemble des fonctions
est l’ensemble des fonctions
![]()
où ![]() .
.
Exercice 3
![]() à résoudre sur
à résoudre sur ![]()
Correction :
Si l’on pose ![]() ,
, ![]() est dérivable et on obtient une équation linéaire du premier ordre
est dérivable et on obtient une équation linéaire du premier ordre ![]() que l’on résout sur
que l’on résout sur ![]() après l’avoir écrite sous la forme
après l’avoir écrite sous la forme ![]() et que l’on note
et que l’on note ![]() .
.
![]() Une primitive de
Une primitive de ![]() est
est ![]() donc la solution générale de l’équation homogène sur
donc la solution générale de l’équation homogène sur ![]() est
est ![]()
![]() il est évident que
il est évident que ![]() est solution de l’équation complète.
est solution de l’équation complète.
Donc la solution générale de ![]() est
est ![]() où
où ![]() .
.
![]() On a posé
On a posé ![]() , donc la fonction
, donc la fonction ![]() doit être à valeurs strictement positives.
doit être à valeurs strictement positives.
![]() si
si ![]() ,
, ![]() est à valeurs strictement positives.
est à valeurs strictement positives.
![]() Si
Si ![]() ,
, ![]() est strictement décroissante sur
est strictement décroissante sur ![]() , admet
, admet ![]() pour limite en
pour limite en ![]() et
et ![]() pour limite en
pour limite en ![]() . Donc
. Donc ![]() est à valeurs strictement positives ssi
est à valeurs strictement positives ssi ![]() .
.
On a donc prouvé que ![]() est à valeurs strictement positives ssi
est à valeurs strictement positives ssi ![]() .
.
La solution générale de l’équation ![]() sur
sur ![]() est donc
est donc
![]() où
où ![]() .
.
⚠️ cet exercice demandait une discussion après avoir déterminé ![]() pour obtenir
pour obtenir ![]() .
.
7. Sur les graphes des solutions d’une équation différentielle
On se place sur ![]() .
.
et soit ![]()
Question 1.
Résoudre l’équation différentielle.
Correction : ![]() On résout l’équation homogène.
On résout l’équation homogène.
![]() admet comme primitive sur
admet comme primitive sur ![]() :
: ![]()
donc ![]() soit
soit ![]() est la solution générale de l’équation homogène.
est la solution générale de l’équation homogène.
![]() On utilise la méthode de variation de la constante
On utilise la méthode de variation de la constante
![]() est solution de
est solution de ![]()
ssi ![]()
ssi ![]()
ssi ![]()
![]() .
.
L’ensemble des solutions est l’ensemble des fonctions ![]() où
où ![]() .
.
Question 2
Déterminer l’ensemble des points des courbes représentatives des solutions à tangente horizontale.
Question 3
Déterminer l’ensemble des points des courbes représentatives où ![]() .
.
8. Équations différentielles d’ordre 2, problème de raccord
exercice 1
![]() .
.
Correction : ![]() La solution générale de l’équation homogène est
La solution générale de l’équation homogène est ![]() où
où ![]() .
.
Il est évident que ![]() est solution particulière sur
est solution particulière sur ![]() de
de ![]() .
.
Donc la solution générale sur ![]() est
est ![]()
où ![]() .
.
![]() Il est évident que
Il est évident que ![]() est solution particulière sur
est solution particulière sur ![]() de
de ![]() .
.
Donc la solution générale sur ![]() est
est ![]()
où ![]() .
.
![]() Recherche d’une solution sur
Recherche d’une solution sur ![]() .
.
On définit ![]()
![]()
![]()
![]() admet
admet ![]() pour limite à gauche en
pour limite à gauche en ![]() et
et ![]() pour limite à droite en
pour limite à droite en ![]() .
.
![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() ssi
ssi ![]() ce que l’on suppose dans la suite.
ce que l’on suppose dans la suite.
On pose alors ![]()
![]() Si
Si ![]()
![]()
![]()
donc ![]()
en utilisant ![]() et
et ![]() .
.
![]() Si
Si ![]() ,
,
![]()
![]()
donc ![]() .
.
![]() 0n en déduit que
0n en déduit que ![]() est dérivable en
est dérivable en ![]() ssi
ssi ![]() ssi
ssi ![]()
ce que l’on suppose dans la suite.
Alors ![]()
![]() Alors
Alors ![]()
![]()
donc ![]()
![]()
![]() Si
Si ![]()
![]()
donc ![]() .
.
![]() Si
Si ![]()
![]()
![]()
donc ![]() .
.
![]() est deux fois dérivable en
est deux fois dérivable en ![]() et
et ![]() .
.
On vérifie ensuite que ![]() , donc
, donc ![]() est solution sur
est solution sur ![]() .
.
Les solutions sont définies par
![]()
![]() où
où ![]() .
.
Exercice 2
![]()
Correction : ![]() Résolution sur
Résolution sur ![]() et
et ![]() .
.
![]() La solution générale de l’équation homogène est
La solution générale de l’équation homogène est ![]() .
.
![]() On cherche une solution particulière sur
On cherche une solution particulière sur ![]() de
de ![]() sous la forme
sous la forme ![]()
![]() est solution sur
est solution sur ![]() ssi
ssi ![]() ssi
ssi ![]() .
.
La solution générale sur ![]() est définie par
est définie par ![]() où
où ![]() .
.
![]() On cherche une solution particulière sur
On cherche une solution particulière sur ![]() de
de ![]() sous la forme
sous la forme ![]()
![]()
![]()
![]()
![]() est solution sur
est solution sur ![]() ssi
ssi ![]() ssi
ssi ![]()
La solution générale sur ![]() est définie par
est définie par ![]() où
où ![]() .
.
![]() Recherche d’une solution sur
Recherche d’une solution sur ![]() .
.
On note ![]()
![]()
![]() admet
admet ![]() pour limite à gauche en
pour limite à gauche en ![]() et
et ![]() pour limite à droite en
pour limite à droite en ![]() .
.
![]() est prolongeable par continuité en
est prolongeable par continuité en ![]() ssi
ssi ![]() ce que l’on suppose dans la suite.
ce que l’on suppose dans la suite.
On pose alors ![]() .
.
![]() Si
Si ![]() ,
,
![]()
donc ![]()
en utilisant ![]() donc
donc
![]() .
.
![]() Si
Si ![]() ,
,
![]()
![]()
![]() .
.
![]() est dérivable en
est dérivable en ![]()
ssi ![]()
ssi ![]()
ssi ![]()
et dans ce cas ![]() , ce que l’on suppose dans la suite.
, ce que l’on suppose dans la suite.
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]()
![]()
![]() .
.
![]() est dérivable en
est dérivable en ![]() ssi
ssi ![]() ssi
ssi ![]() condition déjà introduite.
condition déjà introduite.
Les fonctions solutions sont définies par :
![]() si
si ![]()
et si ![]() ,
,
![]()
où ![]() .
.
9. Résolution d’une équation d’ordre 3 par changement de fonction inconnue
Résoudre sur ![]()
![]()
![]() .
.
Correction :
![]() On note
On note ![]() et on résout l’équation :
et on résout l’équation :
![]()
que l’on écrit
![]()
![]() admet comme primitive
admet comme primitive
![]() donc la solution générale de l’équation homogène est
donc la solution générale de l’équation homogène est ![]()
soit ![]() où
où ![]() .
.
![]() est solution particulière évidente.
est solution particulière évidente.
La solution générale de ![]() est
est ![]() où
où ![]() .
.
![]() On résout maintenant
On résout maintenant ![]()
![]() La solution générale de
La solution générale de ![]() est
est ![]() où
où ![]() .
.
![]() On cherche une solution particulière
On cherche une solution particulière ![]() de
de ![]() sous la forme
sous la forme ![]()
![]()
![]()
![]()
![]() est solution ssi pour tout réel
est solution ssi pour tout réel ![]() ,
,
![]()
ssi ![]() ssi
ssi ![]() .
.
Donc ![]() .
.
Puis ![]() est solution particulière de
est solution particulière de ![]()
soit ![]() .
.
![]()
![]() est solution évidente de
est solution évidente de ![]() .
.
L’ensemble des solutions est l’ensemble des fonctions
![]() où
où ![]() .
.
10. Équations différentielles d’ordre 2, solutions périodiques
Question 1
Quels sont les réels ![]() tels que
tels que ![]() soit périodique de période
soit périodique de période ![]() ?
?
Question 2
On suppose que ![]()
Trouver une CNS pour que toutes les solutions réelles de ![]()
soient périodiques de même période ![]() .
.
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
11. Équations différentielles d’ordre 2, solutions de limite nulle
Question 1
Soient ![]() et
et ![]() , toutes les solutions de
, toutes les solutions de ![]()
admettent ![]() pour limite en
pour limite en ![]()
ssi (![]() et
et ![]() et
et ![]() )
)
ou (![]() et
et ![]() ).
).
Question 2
Soient ![]() et
et ![]() , toutes les solutions réelles de
, toutes les solutions réelles de ![]()
admettent ![]() pour limite en
pour limite en ![]() ssi
ssi ![]() .
.
Soyez sûrs de vos connaissances en vous entraînant sur les divers exercices de cours en ligne de Maths pour les Maths Sup, parmi lesquels :

