Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices et corrigés sur les espaces euclidiens en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Les mathématiques représentent évidemment le coefficient en MP, PC et PSI le plus élevé. Bien que les autres matières enseignées soient également importantes pour entrer dans les meilleures écoles d’ingénieurs, les étudiants de Maths Sup doivent s’assurer dès leur 1ère année de prépa de n’avoir aucune difficulté en mathématiques.
Exercice sur le raisonnement avec un produit scalaire en Maths Sup
Soit ![]() un espace vectoriel euclidien muni d’une base orthonormale
un espace vectoriel euclidien muni d’une base orthonormale ![]() .
.
On donne ![]() une famille de
une famille de ![]() vecteurs de
vecteurs de ![]() .
.
On note ![]() pour tout
pour tout ![]() .
.
Si 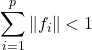 , la famille
, la famille ![]() est une base de
est une base de ![]() .
.
Vrai ou Faux ?
Exercice sur un produit scalaire canonique sur 
Question 1 : Une inégalité entre traces
![]() ,
, ![]()
Vrai ou Faux ?
Question 2 : Un orthogonal
Quel est l’orthogonal de ![]() ?
?
Question 3 : Distance de ![]() à
à ![]()
Calculer le carré de la distance de ![]() à
à ![]() .
.
Exercice sur un produit scalaire sur ![Rendered by QuickLaTeX.com \mathbb{R} _ n [\textrm{X}]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2043%2018%22%3E%3C/svg%3E)
On se place sur ![]() .
.
Question 1 :
Si ![]() est l’ensemble des polynômes
est l’ensemble des polynômes ![]() tels que
tels que 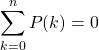 , déterminer
, déterminer ![]() .
.
Question 2 :
Déterminer une base orthonormale de ![]() .
.
Exercice sur l’écriture d’une matrice de projection orthogonale
On se place dans ![]() muni du produit scalaire canonique.
muni du produit scalaire canonique.
On considère le sous espace ![]() défini par
défini par ![]()
Question :
Déterminer une base de ![]() , puis une base orthonormale.
, puis une base orthonormale.
Exercice sur les projections orthogonales en Maths Sup
Soient ![]() et
et ![]() deux sous-espaces vectoriels de dimension finie.
deux sous-espaces vectoriels de dimension finie.
On suppose que ![]() .
.
Question 1 :
Caractériser ![]() .
.
Question 2 :
On suppose toujours ![]() .
.
![]()
Vrai ou Faux ?
Exercice sur les coefficients d’une matrice orthogonale en Maths Sup
Soit ![]() ,
, ![]() .
.
Question 1 :
a) 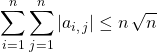 .
.
Vrai ou Faux ?
Question 2 :
Le cas d’égalité ?
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
Correction de l’exercice sur le raisonnement avec un produit scalaire
Vrai,
Soient ![]() tel que
tel que ![]() .
.
On note ![]() .
.
On introduit ![]() tel que
tel que ![]()
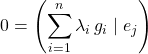
![]()
![]()
donc 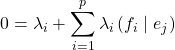
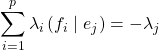
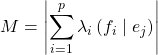
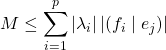 .
.
Par l’inégalité de Cauchy-Schwarz,
![]()
donc ![]() et
et ![]() ,
,
alors 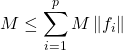 .
.
Soit 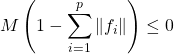 .
.
Comme 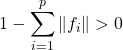 , on en déduit que
, on en déduit que ![]() .
.
Donc ![]() .
.
![]() est une famille libre de
est une famille libre de ![]() vecteurs dans un ev de dimension
vecteurs dans un ev de dimension ![]() , c’est une base de
, c’est une base de ![]() .
.
Corrections sur un produit scalaire canonique sur 
Question 1 : Une inégalité entre traces
Vrai,
Par utilisation de l’inégalité de Cauchy-Schwarz, avec les matrices ![]() et
et ![]() ,
,
![]() ce qui s’écrit
ce qui s’écrit
![]() .
.
Il y a égalité ssi la famille ![]() est liée ssi
est liée ssi ![]() est combinaison linéaire de
est combinaison linéaire de ![]()
Question 2 : Un orthogonal
Tr est une forme linéaire non nulle sur ![]() .
. ![]() est un hyperplan de
est un hyperplan de ![]() .
.
![]() est une droite.
est une droite.
Pour tout ![]() ,
, ![]() , donc
, donc ![]() , ce qui prouve que
, ce qui prouve que ![]() est l’orthogonal de l’hyperplan
est l’orthogonal de l’hyperplan ![]() .
.
Question 3 : Distance de ![]() à
à ![]()
On détermine la projection orthogonale ![]() sur
sur ![]() engendré par
engendré par ![]() ,
,
![]() soit
soit ![]()
Par le théorème de Pythagore,
![]()
![]() .
.
On rappelle que pour déterminer la projection orthogonale ![]() sur un hyperplan
sur un hyperplan ![]() , on introduit
, on introduit ![]() tel que
tel que ![]() .
.
La projection orthogonale ![]() sur la droite engendrée par
sur la droite engendrée par ![]() est définie par
est définie par ![]() . Alors
. Alors ![]() .
.
Correction de l’exercice sur le produit scalaire sur ![Rendered by QuickLaTeX.com \mathbb{R} _ n [\textrm{X}]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2043%2018%22%3E%3C/svg%3E)
Question 1 :
On remarque que ![]() ssi
ssi ![]()
Donc ![]() est un sous-espace vectoriel de
est un sous-espace vectoriel de ![]() et c’est l’orthogonal de
et c’est l’orthogonal de ![]() .
.
C’est un hyperplan (de dimension ![]() car
car ![]() ).
).
Question 2 :
On utilise le procédé d’orthonormalisation de Gram-Schmidt sur la base ![]() de
de ![]() .
.
![]() On a déjà vu que
On a déjà vu que ![]() .
.
On pose ![]() .
.
![]() Soit
Soit ![]()
![]()
On avait calculé : ![]()
![]() .
.
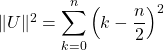
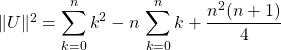
![]()
![]()
![]()
![]() Puis
Puis ![]()
![]() .
.
![]() est une base orthonormale de
est une base orthonormale de ![]() .
.
Correction sur l’écriture d’une matrice de projection orthogonale
![]() Recherche d’une base de
Recherche d’une base de ![]()
Soit ![]() .
.
![]() ssi
ssi ![]()
ssi ![]()
ssi ![]()
![]() .
.
Alors ![]() avec
avec ![]() et
et ![]() .
.
![]() On utilise le procédé d’orthonormaisation de Gram-Schmidt
On utilise le procédé d’orthonormaisation de Gram-Schmidt
![]()
![]() , on note donc
, on note donc ![]() .
.
![]() Soit
Soit ![]()
![]()
![]()
![]()
donc ![]() .
.
Conclusion : Une base orthonormale de ![]() est
est ![]() avec
avec
![]()
![]() .
.
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
Correction d’exercice sur les projections orthogonales
Question 1 :
![]() Si
Si ![]() ,
, ![]() et
et ![]() donc
donc ![]() alors
alors ![]() , ce qui prouve que
, ce qui prouve que ![]() .
.
![]() Si
Si ![]() ,
, ![]()
![]() en utilisant Q1.b) pour
en utilisant Q1.b) pour ![]() puis
puis ![]() ,
,
Par double inégalité, ![]() , par Q1a),
, par Q1a), ![]() ; alors
; alors ![]() donc
donc ![]() .
.
On a prouvé que ![]() , donc
, donc ![]() .
.
![]()
![]() Par double inclusion,
Par double inclusion, ![]() .
.
Question 2 :
Vrai,
Soit ![]() .
.
Comme ![]() est une projection orthogonale,
est une projection orthogonale, ![]() soit
soit ![]()
![]()
puis ![]()
soit ![]()
donc ![]() .
.
Sachant que ![]() , pour tout
, pour tout ![]() ,
, ![]() ,
,
soit ![]() .
.
Correction d’exercice sur les coefficients d’une matrice orthogonale
Question 1 :
Vrai,
On utilise le produit scalaire canonique sur ![]() :
: ![]() .
.
On définit la matrice ![]() par
par ![]() si
si ![]() et
et ![]() si
si ![]() , alors
, alors ![]() .
.
![]() avec
avec ![]() où
où ![]() , donc
, donc ![]() .
.
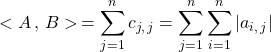
Par interversion des signes somme :
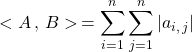 .
.
Puis par l’inégalité de Cauchy-Schwarz :
![]()
![]() .
.
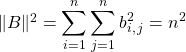 .
.
donc ![]() , ce que l’on voulait démontrer.
, ce que l’on voulait démontrer.
Question 2 :
S’il y a égalité, l’inégalité de Cauchy-Schwarz ![]() est une égalité ce qui est équivalent à
est une égalité ce qui est équivalent à ![]() est une famille liée
est une famille liée
ssi ![]()
ssi ![]() .
.
On obtient une condition équivalente en multipliant chaque égalité par le réel non nul ![]() et en utilisant
et en utilisant ![]() et
et ![]() .
.
Il y a égalité ssi ![]()
![]() et
et ![]() donnent
donnent ![]() .
.
On a donc prouvé qu’il y a égalité ssi ![]() est une matrice orthogonale telle que
est une matrice orthogonale telle que ![]() .
.
Pour espérer avoir de très bons résultats à Centrale Supélec, Mines-Pont, Mines-Télécom ou encore à l’X ou l’ENS, les étudiants de Maths Sup peuvent s’entraîner avec les exercices des cours en ligne avant de passer à la préparation des concours sur les annales. Bien connaître son cours et réussir les exercices de cours est primordial avant de se lancer sur les exercices des annales. Ainsi, les étudiants de PTSI, PCSI et MPSI ont à leur disposition tous les chapitres de Maths au programme sous forme de cours ligne, dont :

