Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Chapitres Maths en MPSI, PCSI, MP2I, PTSI
Exercices corrigés sur les Fractions rationnelles en Maths Sup
Résumé de cours Exercices et corrigés
Cours en ligne de Maths en Maths Sup
Plan des exercices : Polynome
1. Des calculs simples
2. Un peu plus compliqués
3. Avec des polynômes de degré n
COURS DE MATHS
Les meilleurs professeurs particuliers
Pour progresser et réussir
Avis Google France ★★★★★ 4,9 sur 5
1. Des calculs simples sur les fractions rationnelles en maths sup
Exercice 1
Décomposition en éléments simples de ![]()
Correction :
![]() est une fraction rationnelle irréductible de degré 0, ayant trois pôles simples.
est une fraction rationnelle irréductible de degré 0, ayant trois pôles simples.
Sa partie entière est égale à 1 (quotient de deux polynômes unitaires de degré 3).
Il existe trois réels ![]() tels que
tels que
![]() .
.
On obtient ![]() en évaluant en
en évaluant en ![]()
![]() ,
,
donc ![]() .
.
De même, ![]() et
et ![]() .
.
![]() .
.
Exercice 2
Décomposition en éléments simples dans ![]() de
de ![]() .
.
Correction :
![]() est une fraction irréductible de degré 1, admettant un pôle double
est une fraction irréductible de degré 1, admettant un pôle double ![]() et un pôle simple
et un pôle simple ![]() .
.
![]() Il y a une partie entière
Il y a une partie entière ![]() qui est le quotient de
qui est le quotient de ![]() par
par ![]()
On pose l’opération et on obtient un quotient égal à ![]() et un reste égal à
et un reste égal à ![]() .
.
![]() La décomposition formelle de la fraction
La décomposition formelle de la fraction ![]() s’écrit
s’écrit
![]()
![]() .
.
![]() en multipliant la relation par
en multipliant la relation par ![]() et en évaluant
et en évaluant ![]() en
en ![]() , on obtient
, on obtient
![]()
![]() en multipliant la relation par
en multipliant la relation par ![]() et en évaluant
et en évaluant ![]() en
en ![]() ,
,
![]()
![]() On évalue la relation en
On évalue la relation en ![]() :
:
![]()
![]() ,
, ![]()
![]()
![]() .
.
Exercice 3
Décomposition en éléments simples de ![]()
Correction : ![]() est une fraction rationnelle irréductioble, sans partie entière et ayant deux pôles doubles.
est une fraction rationnelle irréductioble, sans partie entière et ayant deux pôles doubles.
Il existe 4 réels ![]() tels que
tels que ![]()
![]()
On obtient ![]() en évaluant en
en évaluant en ![]()
![]()
donc ![]() .
.
De même, ![]() .
.
On détermine ensuite la limite en ![]() de
de ![]() et on obtient
et on obtient ![]() .
.
Et en évaluant en ![]() :
:
![]()
ce qui donne
![]() et
et ![]()
ssi ![]() et
et ![]() .
.
![]()
![]()
Exercice 4
Décomposition en éléments simples dans ![]() de
de ![]() .
.
Correction : ![]() est irréductible, sans partie entière et la décomposition dans
est irréductible, sans partie entière et la décomposition dans ![]() du dénominateur est :
du dénominateur est :
![]() .
.
Il existe trois réels ![]() tels que
tels que
![]()
![]()
On obtient ![]() en évaluant
en évaluant ![]() en
en ![]() , donc
, donc ![]() .
.
On détermine ensuite la limite en ![]() de
de ![]() et on obtient
et on obtient ![]() soit
soit ![]() .
.
Puis on évalue en ![]() :
: ![]() soit
soit ![]() .
.
Donc ![]() .
.
2. un peu plus compliqués
Exercice 1
Décomposer en éléments simples dans ![]() , puis
, puis ![]() ,
, ![]() .
.
Correction : ![]() est une fraction rationnelle irréductible, de degré égal à
est une fraction rationnelle irréductible, de degré égal à ![]() admettant un pôle double
admettant un pôle double ![]() et deux pôles complexes conjugués
et deux pôles complexes conjugués ![]() et
et ![]() .
.
![]() Décomposition dans
Décomposition dans ![]() .
.
![]() On obtient une décomposition formelle en éléments simples de la forme
On obtient une décomposition formelle en éléments simples de la forme
![]() .
.
C’est une fraction rationnelle à coefficients dans ![]() avec deux pôles conjugués, donc
avec deux pôles conjugués, donc ![]() .
.
![]()
![]() est paire
est paire
![]()
c’est la décomposition en éléments simples de ![]() , donc par unicité :
, donc par unicité :
![]() ,
, ![]() , alors
, alors ![]() et
et ![]() , donc
, donc ![]() est un imaginaire pur.
est un imaginaire pur.
Par propriété des pôles simples : ![]() .
.
En utilisant ![]() et en substituant
et en substituant ![]() à
à ![]() , on obtient
, on obtient ![]()
alors ![]() .
.
![]() Décomposition dans
Décomposition dans ![]() .
.
Pour trouver la décomposition en éléments simples dans ![]() , on réduit au même dénominateur
, on réduit au même dénominateur
![]()
![]()
![]() et
et ![]() .
.
Exercice 2
Décomposer en éléments simples dans ![]() puis
puis ![]() la fraction
la fraction
![]()
Correction : ![]()
![]() Décomposition dans
Décomposition dans ![]() .
.
C’est une fraction irréductible, sans partie entière et admettant 4 pôles simples : ![]() .
.
Comme ![]() est à coefficients réels, sa décomposition en éléments simples s’écrit
est à coefficients réels, sa décomposition en éléments simples s’écrit
![]()
On obtient la valeur de ![]() en évaluant
en évaluant ![]() en
en ![]() :
:
![]() .
.
On obtient la valeur de ![]() en évaluant en
en évaluant en ![]() en
en ![]() .
.
On rappelle que ![]() et
et ![]() .
.
![]()
![]()
![]() .
.
donc ![]()
![]() .
.
![]() Décomposition dans
Décomposition dans ![]() .
.
![]()
![]() par réduction au même dénominateur .
par réduction au même dénominateur .
![]()
![]()
![]()
![]()
![]()
![]()
donc
![]()
![]() .
.
![]() .
.
Exercice 3
Décomposer en éléments simples sur ![]() puis
puis ![]() la fraction
la fraction ![]()
Correction : ![]() Décomposition sur
Décomposition sur ![]() .
.
![]() est une fraction rationnelle paire, écrite sous forme irréductible et admettant 4 pôles qui sont tous simples et qui sont les racines
est une fraction rationnelle paire, écrite sous forme irréductible et admettant 4 pôles qui sont tous simples et qui sont les racines ![]() -ièmes de
-ièmes de ![]() .
.
En notant ![]() ,
, ![]() , donc les racines
, donc les racines ![]() -ièmes de
-ièmes de ![]() sont
sont ![]() .
.
La décomposition de ![]() s’écrit
s’écrit
![]()
avec ![]() .
.
Comme ![]() ,
, ![]()
et ![]()
donc ![]()
Puis ![]()
donc ![]() .
.
Le pôle conjugué de ![]() est
est ![]() , comme la fraction est à coefficients réels,
, comme la fraction est à coefficients réels, ![]() .
.
Puis comme ![]() est paire,
est paire, ![]()
donne
![]()
![]()
donc par unicité de la décomposition en éléments simples :
![]() et
et ![]() .
.
soit ![]()
avec ![]()
![]() Décomposition sur
Décomposition sur ![]() .
.
Il est plus simple ensuite de remarquer que ![]()
donc ![]()
![]()
et que :
![]()
![]()
pour obtenir par division la décompostio de ![]() :
:
![]()
COURS PARTICULIERS EN LIGNE
Nous avons sélectionné pour vous les meilleurs professeurs particuliers.
POUR ACCÉLÉRER MA PROGRESSION
Avis Google France ★★★★★ 4,9 sur 5
3. où il y a des polynômes de degré 
Exercice 1
Soit ![]() où
où ![]() ,
, ![]() ayant
ayant ![]() racines réelles distinctes et non nulles
racines réelles distinctes et non nulles ![]() avec
avec 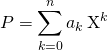
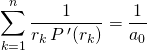 . Vrai ou faux ?
. Vrai ou faux ?
Correction : On décompose en éléments simples dans ![]() la fraction rationnelle
la fraction rationnelle ![]() qui est irréductible, de degré strictement négatif et admet
qui est irréductible, de degré strictement négatif et admet ![]() pôles distincts.
pôles distincts.
On obtient une décomposition de la forme 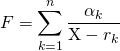
avec ![]()
donc 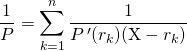 .
.
On peut évaluer la relation en ![]() car
car ![]() n’est pas pôle de la fraction :
n’est pas pôle de la fraction :
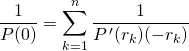
donc 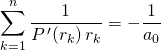 .
.
Exercice 2
Soit ![]() où
où ![]() ,
, ![]() ayant n racines réelles distinctes et non nulles
ayant n racines réelles distinctes et non nulles ![]() où
où 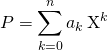 et
et ![]() ,
,
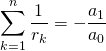 . Vrai ou Faux ?
. Vrai ou Faux ?
Correction :
![]() est le quotient de deux polynômes de degré
est le quotient de deux polynômes de degré ![]() dont les coefficients dominants sont
dont les coefficients dominants sont ![]() et
et ![]() . Elle admet
. Elle admet ![]() comme partie entière.
comme partie entière.
Les racines de ![]() sont distinctes (donc ne sont pas racines de
sont distinctes (donc ne sont pas racines de ![]() ) et
) et ![]() est racine de
est racine de ![]() mais n’est pas racine de
mais n’est pas racine de ![]() ), donc
), donc ![]() est écrite sous forme irréduc- tible.
est écrite sous forme irréduc- tible.
On obtient donc
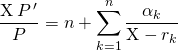
avec ![]()
donc 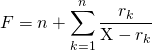 .
.
En dérivant sur ![]() , la fonction rationnelle
, la fonction rationnelle ![]() , on obtient
, on obtient
![]()
et 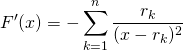
en évaluant en ![]() qui n’est pas pôle de
qui n’est pas pôle de ![]() ,
, 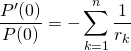
soit 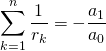 .
.
Exercice 3
question 1.
Soit ![]() un polynôme de degré
un polynôme de degré ![]() scindé sur
scindé sur ![]() , quelle est la décomposi- tion en éléments simples de
, quelle est la décomposi- tion en éléments simples de ![]() ?
?
Correction :
Si 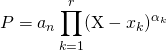 , il suffit de remarquer que :
, il suffit de remarquer que :
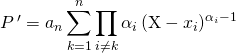
donc 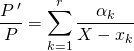 .
.
🧡 C’est un calcul classique à savoir refaire.
Question 2
On suppose que ![]() est scindé sur
est scindé sur ![]() .
.
![]() . Vrai ou faux ?
. Vrai ou faux ?
Correction : On note ![]() .
.
On dérive la relation définie sur ![]() par
par
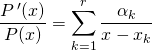 .
.
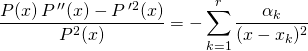 .
.
donc
![]()
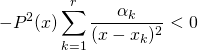 .
.
comme opposé du produit de deux réels strictement positifs
Puis si ![]() ,
, ![]()
donc ![]() .
.
Alors ![]() .
.
Exercice 4
Soit ![]() .
.
Décomposer en éléments simples
![]()
On peut en déduire que 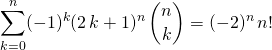
Vrai ou faux ?
Correction : ![]() est une fraction rationnelle de degré
est une fraction rationnelle de degré ![]() (quotient de deux polynômes unitaires de degré
(quotient de deux polynômes unitaires de degré ![]() ), irréductible de pôles simples
), irréductible de pôles simples ![]() où
où ![]() .
.
La partie entière est le quotient du numérateur par le dénominateur, elle est égale à 1.
On peut donc écrire
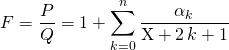 .
.
Soit ![]() et
et ![]() avec
avec ![]()
alors ![]()
![]() ,
,
ce que l’on peut écrire :
![]()
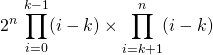
en posant ![]() dans le premier produit et
dans le premier produit et ![]() dans le deuxième :
dans le deuxième :
![]()
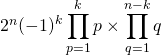
![]()
et ![]()
que l’on peut écrire
![]() .
.
En évaluant en ![]() :
: 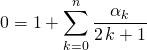
soit 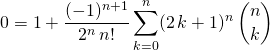
donc 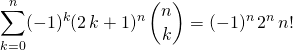
Exercice 5
Soit ![]() ,
, ![]() .
.
Si ![]() , on note
, on note ![]()
Quelle est la valeur de 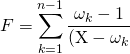 ?
?
Exercice 6
Si ![]() , décomposition en éléments simples de
, décomposition en éléments simples de ![]() dans
dans ![]() puis
puis ![]() .
.
Les cours en ligne sont un très bon complément aux cours enseignés en cours en Maths Sup, mais également un bon complément aux cours particuliers ou aux stages intensifs de révision. En effet, il vous est possible de réviser et de vous entraîner sur différents chapitres de Maths en MPSI, PCSI ou PTSI en fonction de vos envies et de votre temps. Ainsi, vous pouvez par exemple choisir de vous entraîner sur :

